Trong đại số và hình học giải tích, một trong những khái niệm quan trọng nhất là định thức ma trận. Nắm vững khái niệm này sẽ giúp chúng ta hiểu sâu hơn về cấu trúc và tính chất của ma trận, giúp giải quyết các bài toán phức tạp. Sau đây, hãy cùng TTnguyen tìm hiểu về cách tính định thức ma trận nhé.
Xem thêm:
tính định thức của ma trận cấp 4
1. Định thức ma trận là gì?
Định thức ma trận là một giá trị số được gán cho ma trận vuông. Det ma trận được biểu diễn bằng hai dòng dọc hoặc đơn giản bằng cách viết det và viết tên ma trận. ví dụ. |A|, det (A), det A.
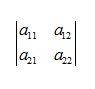
=> Công thức thức tính giá trị của det ma trận vuông cấp 2: |A| = \(a_{11}.a_{22}-a_{21}.a_{12}\)
Ví dụ 1: Tính định thức bậc 2 sau:
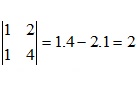
Liên quan:
2. Công thức tính định thức
- Công thức tính det cấp 2
- |A|= \(a_{11}.a_{22}-a_{21}.a_{12}\)
- Công thức định thức cấp 3 (quy tắc Sarius):

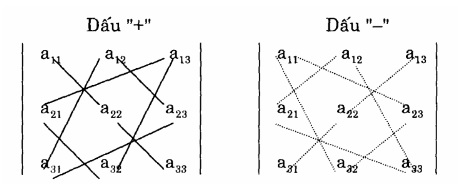
Ví dụ 2: Giải định thức ma trận bằng phương pháp tam giác
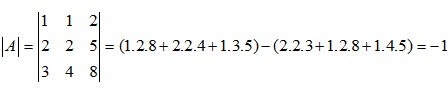
3. Định thức con chính
Khái niệm: Định thức con là một ma trận con được tạo thành bằng cách chọn một số hàng và một số cột từ ma trận A ban đầu và xoá bỏ các hàng các cột còn lại.
Cho det của ma trận cấp 4 là: \(\begin{vmatrix}
1& 2& 3& 4 \\
1& 3& 4& 5\\
3& 4& 5& 6\\
5& 6& 7& 8
\end{vmatrix}\)
Ta có:
+ Định thức con chính cấp 1: \(\begin{vmatrix}
1
\end{vmatrix}\)
+ Định thức con chính cấp 2: \(\begin{vmatrix}
1& 2 \\
1& 3
\end{vmatrix}\)
+ Định thức con chính cấp 3: \(\begin{vmatrix}
1& 2& 3 \\
1& 3& 4 \\
3& 4& 5
\end{vmatrix}\)
+ Định thức con chính cấp 4: \(\begin{vmatrix}
1& 2& 3& 4 \\
1& 3& 4& 5\\
3& 4& 5& 6\\
5& 6& 7& 8
\end{vmatrix}\)

4. Các tính chất của định thức
Dưới đây là một số tính chất cơ bản:
- Tính chất 1: det ( \(A^{T}\)) = det (A).
- Tính chất 2: Đổi chỗ hai hàng ( hai cột ) của định thức cho nhau thì định thức đổi dấu.
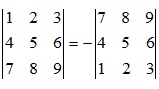
- Tính chất 3: Khi nhân các phần tử của một hàng (một cột ) với cùng một số k thì định thức được nhân lên k lần.
- Tính chất 4: Khi tất cả các phần tử của một hàng (một cột) có dạng tổng của hai số hạng thì định thức có thể phân tích thành tổng của hai định thức như sau:
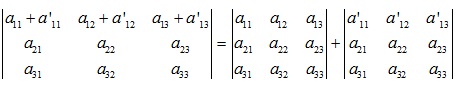
- Tính chất 5: Định thức sẽ bằng không nếu thoả mãn một trong các điều kiện sau:
– Có một hàng (một cột) gồm toàn là số không.
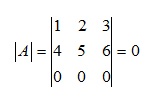
– Có hai hàng (hai cột) giống nhau.
– Có một hàng (một cột) tỉ lệ vơi nhau.
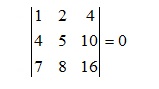
- Tính chất 6: Định thức của ma trận sẽ không thay đổi nếu nhân k vào một hàng (một cột) rồi đem cộng vào một hàng khác (cột khác).
- Tính chất 7: Định thức của ma trận tam giác bằng tích các phần tử chéo.
- Tính chất 8: Nếu 2 ma trận vuông cấp n thì det (A.B) = det(A).det(B).
- Tính chất 9: Nếu A là ma trận vuông cấp n thì det (kA) = \(k^{n}\) .det (A).Ví dụ: \(A_{3×3}\) , det(A) = 5 ⇒ det(2A) = \(2^{3}.5\)= 40
- Tính chất 10: Rút nhân tử chung của 1 hàng, 1 cột ra ngoài định thức:
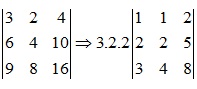
Xem thêm: phép nhân 2 ma trận trong toán cao cấp
5. Tính định thức bằng phép biến đổi siêu cấp
Dưới đây là một số ví dụ tính định thức bằng cách triển khai theo hàng:
Ví dụ 3: Tính định thức ma trận
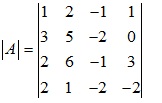
Giải:
Các bước thực hiện:
- Nhân hàng 1 với -3 vào hàng 2 để xuất hiện phần tử 0
- a21=(-3).1 + 3 =0
- a22=(-3).2+5=-1
- a23=(-3).(-1)+(-2)=1
- a24=(-3).1+0=-3
- Tương tự nhân hàng 1 với -2 vào hàng 3, nhân hàng 1 với -2 vào hàng 1 ta được

- Nhân hàng 2 với 2 vào hàng 3 để xuất hiện phần tử 0
- Nhân hàng 2 với 3 vào hàng 4, ta được
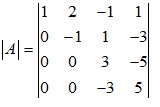
- Nhân hàng 3 với 1 vào hàng 4, ta được
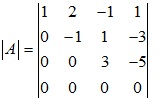
- Như vậy định thức A chính là tích đường chéo: 1.(-1).3.0=0
Bài viết liên quan:
6. Bài tập định thức có lời giải
Bài 1: Tính định thức cấp 2 sau:
![]()
![]()
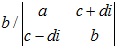
![]()
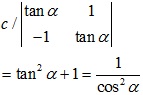
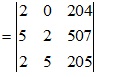
Bài 2: Biết các số 204,527,255 chia hết cho 17. Chứng minh định thức d chia hết cho 17

Giải
Nhân cột thứ nhất với 100 rồi cộng vào cột cuối
Nhân cột thứ hai với 10 rồi cộng vào cột cuối
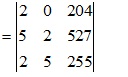

Kết luận định thức chia hết cho 17 vì tích có thừa số 17.
Bài 3: Cho a là ma trận vuông cấp 3 có det(a) = 3. định thức 2a là
Hướng dẫn giải
Áp dụng công thức: (kA) = \(k^{n}\) .det (A)
Ta có: det(a) = 3 ⇒ det(2a) = \(2^{3}.3\)= 24
7. Ứng dụng của định thức
Trong đại số tuyến tính, định thức thường được tính bằng cách sử dụng các phần tử của ma trận vuông. Tính định thức được sử dụng để giải quyết giải hệ phương trình tuyến tính, tính ma trận nghịch đảo của ma trận,…
Câu hỏi liên quan
Định thức bằng 0 khi nào?
Một ma trận có định thức bằng 0 khi và chỉ khi nó không khả nghịch, tức là không tồn tại ma trận nghịch đảo của nó. Một số trường hợp thường gặp khi ma trận có định thức bằng 0 là:
- Ma trận không vuông: Một ma trận không vuông khi số hàng khác số cột.
- Hệ phương trình tuyến tính vô nghiệm hoặc vô số nghiệm: Nếu một hệ phương trình tuyến tính có nhiều hơn một nghiệm hoặc không có nghiệm nào, ma trận hệ số của hệ phương trình đó sẽ có định thức bằng 0.
Định thức có âm không?
Có, định thức có thể là một giá trị âm.
Khi lấy một hàng của định thức nhân lên với số k rồi cộng vào một hàng khác thì định thức sẽ
Khi lấy một hàng của ma trận định thức, nhân nó với một số k và cộng vào một hàng khác, det sẽ không thay đổi.
Chúng ta sẽ xem xét một ví dụ cụ thể để minh họa việc lấy một hàng của định thức, nhân nó với một số k và cộng vào một hàng khác.
Xét ma trận sau: \(\begin{vmatrix}
1& 2 \\
3& 4
\end{vmatrix}\)
Định thức này bằng (1*4) – (3*2) = -2
Bây giờ, chúng ta lấy hàng đầu tiên của ma trận A (hàng 1), nhân nó với số k = 2 và cộng vào hàng thứ hai. Kết quả sẽ là ma trận B:
\(\begin{vmatrix}1& 2 \\
5& 8
\end{vmatrix}\)
Định thức B cũng được tính bằng (1*8)-(5*2) = -2
Như bạn có thể thấy, det B không thay đổi so với định thức ban đầu của ma trận A.
Khi định thức có hai hàng tỉ lệ nhau thì định thức sẽ
Khi hai hàng của ma trận tỉ lệ nhau nghĩa là một hàng có thể thu được bằng cách nhân một hằng số với hàng còn lại, thì định thức sẽ bằng 0.
Ứng dụng của định thức
Trong đại số tuyến tính, định thức thường được tính bằng cách sử dụng các phần tử của ma trận vuông. Tính định thức được sử dụng để giải quyết giải hệ phương trình tuyến tính, tính ma trận nghịch đảo của ma trận,…
Tải file tài liệu lý thuyết và bài tập vận dụng định thức ma trận PDF
Trên đây là một vài lý thuyết cơ bản cùng cách giải định thức ma trận 3×3, tính định thức 4×4, tính định thức 5×5. Nếu có bất kì thắc mắc nào thì đừng ngần ngại liên hệ với mình nhé. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net
Bài viết liên quan:
- Bài tập chéo hoá ma trận có lời giải
- ma trận kề
- bài tập tìm giá trị riêng và vectơ riêng có lời giải chi tiết
- bài tập dạng toàn phương
- không gian vecto con
- tìm cơ sở và số chiều của không gian vecto