Bài viết dưới TTnguyen sẽ chia sẻ một số lý thuyết cơ bản cùng với các dạng bài tập về độc lập tuyến tính và phụ thuộc tuyến tính trong chương trình toán cao cấp môn đại số và hình học giải tích.
Xem thêm:
1. Độc lập tuyến tính và phụ thuộc tuyến tính là gì?
- Một hệ các vectơ {v1,…,vn} trong không gian vectơ V được gọi là phụ thuộc tuyến tính, nếu tồn tại các số: k1,…, kn không đồng thời bằng 0 sao cho:
k1 v1 +… + kn vn = 0.
- Hệ các vectơ là độc lập tuyến tính khi và chỉ khi phương trình vectơ:
k1 v1 +… + kn vn = 0 chỉ có nghiệm duy nhất: k1 = k2 =… = kn = 0
1.1 Hình ảnh độc lập tuyến tính
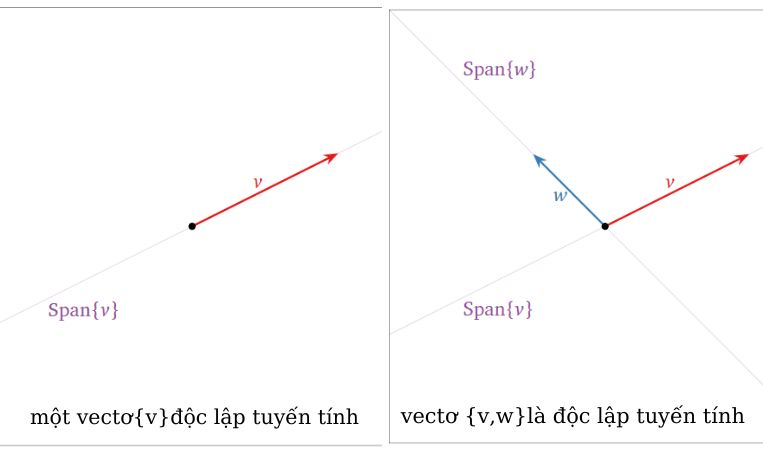
1.2 Hình ảnh phụ thuộc tuyến tính

2. Cách chứng minh độc lập tuyến tính và phụ thuộc tuyến tính
- Điều kiện độc lập tuyến tính, phụ thuộc tuyến tính với ma trận vuông:
- Nếu định thức ma trận =0 => có vô số nghiệm => phụ thuộc tuyến tính ( nghiệm không tầm thường)
- Nếu định thức ≠ 0 => có nghiệm duy nhất => độc lập tuyến tính
- Điều kiện với ma trận thường: Biến đổi siêu cấp về ma trận bậc thang
- Nếu có nghiệm duy nhất => độc lập tuyến tính
- Nếu có vô số nghiệm => phụ thuộc tuyến tính
3. Các định lí về độc lập tuyến tính và phụ thuộc tuyến tính
| Phụ thuộc tuyến tính | Độc lập tuyến tính |
|---|---|
| Mọi tập hợp chứa vectơ 0 đều phụ thuộc tuyến tính, tức là nếu 0 ∈ S thì S phụ thuộc tuyến tính. | Mọi tập hợp độc lập tuyến tính thì không chứa vectơ 0, tức là nếu S là tập con độc lập tuyến tính của V thì vectơ 0 ∉ S. |
| Mọi tập hợp chứa tập con phụ thuộc tuyến tính thì nó phụ thuộc tuyến tính, tức là nếu E ⊂F và E phụ thuộc tuyến tính thì F phụ thuộc tuyến tính. | Mọi tập con khác rỗng của một tập độc lập tuyến tính thì độc lập tuyến tính. Tức là Ø ≠ E ⊂ F và F độc lập tuyến tính thì E độc lập tuyến tính. |
| Tập S={u1,u2,…,um} (m≥2) phụ thuộc tuyến tính khi và chỉ khi tồn tại vectơ ui ∈ S sao cho ui là tổ hợp tuyến tính của các vectơ còn lại trong S. | Tập S ≠ Ø độc lập tuyến tính khi và chỉ khi mỗi vectơ bất kỳ u ∈ S đầu không thể là tổ hợp tuyến tính của các vectơ còn lại trong S. |
| Mọi tập khác rỗng S ⊂ V thì hoặc S độc lập tuyến tính hoặc S phụ thuộc tuyến tính. | |
Tóm lại:
- Hai vectơ phụ thuộc tuyến tính nếu và chỉ khi chúng thẳng hàng, tức là một vectơ là bội số vô hướng của vectơ kia.
- Bất kỳ tập hợp nào chứa vectơ 0 đều phụ thuộc tuyến tính.
- Nếu một tập hợp con của{v1,v2,…,vk}là phụ thuộc tuyến tính, sau đó{v1,v2,…,vk}cũng phụ thuộc tuyến tính.
4. Bài tập về độc lập tuyến tính và phụ thuộc tuyến tính có lời giải
Ví dụ 1: Xét sự độc lập tuyến tính, phụ thuộc tuyến tính của hệ vectơ
Bài 1: Xét sự độc lập tuyến tính, phụ thuộc tuyến tính: S={2-x,2x-x2,6-5x+x2 }
Giải
Xét hệ phương trình sau:

Đổi chỗ các phương trình để thuận tiện cho việc tính toán

Xét ma trận bổ sung của phương trình
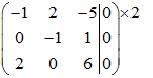
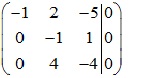
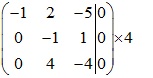

![]()
Cách 2: Vì ma trận A vuông => detA=((-1).(-1).6+2.2.1)-(2.-1.-5)=0 => phụ thuộc tuyến tính
Bài viết liên quan:
Bài 2: xét tính độc lập tuyến tính phụ thuộc tuyến tính




Bài 3: xét sự độc lập tuyến tính của hệ vectơ



Bài 4: Xét sự phụ thuộc tuyến tính


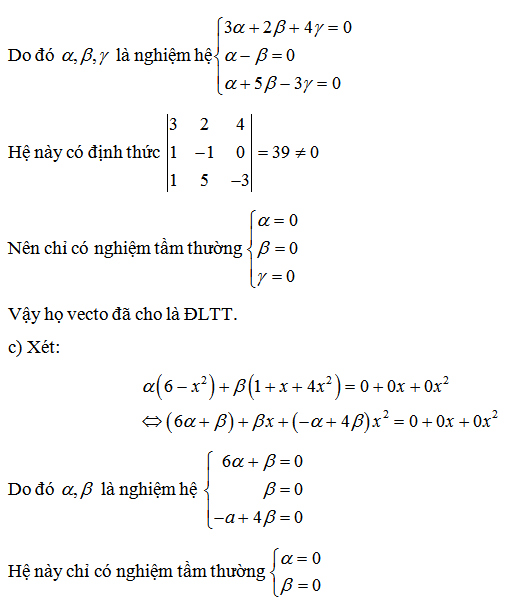

Ví dụ 2: Chứng minh hệ vectơ độc lập tuyến tính
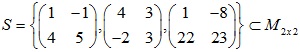
Giải
Xét ma trận bổ sung sau:
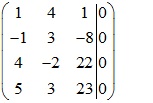
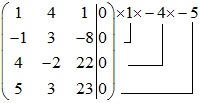
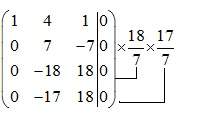
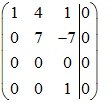

![]()
Ví dụ 3: Kiểm tra các tập sau đây phụ thuộc tuyến tính hay độc lập tuyến tính:
1.u1=(1,2) và u2=(-3,-6) trong R2
=> Phụ thuộc tuyến tính vì u1=-3u2
2.u1=(1,2,3) và u2=(3,6,7) trong R3
=> Độc lập tuyến tính
3.u1=(4,-2,6) và u2=(6,-3,9) trong R3
Xét ma trận bổ sung:
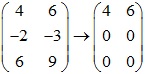
=> vô số nghiệm=> phụ thuộc tuyến tính
4.u1=(5,4,3), u2=(3,3,2), u2=(8,1,3) trong R3
Xét ma trận bổ sung:
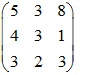
det=45+64+9-72-10-36=0 => phụ thuộc tuyến tính
5. 1+3x+3x2, x+4x2, 5+6x+3x2, 7+2x-x2 trong P2
=> phụ thuộc tuyến tính
6. Tệp nào phụ thuộc tuyến tính dưới đây:

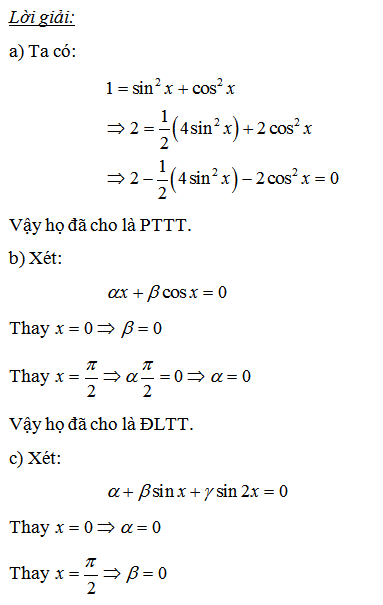


7. Tệp nào phụ thuộc tuyến tính



Ví dụ 4: Tìm m để hệ 4 vectơ độc lập tuyến tính
X1=(4,4,2,8); X2=(3,1,0,4); X3=(-2,4,-4,-6); X4=(4,9,2,m−1)
Hướng dẫn giải

Tài liệu độc lập tuyến tính và phụ thuộc tuyến tính PDF:
Câu hỏi thường gặp
Điều kiện độc lập tuyến tính
Nếu có nghiệm duy nhất => độc lập tuyến tính
Điều kiện phụ thuộc tuyến tính
Nếu có vô số nghiệm => phụ thuộc tuyến tính
Vừa rồi mình đã tổng hợp các bài toán độc lập tuyến tính và phụ thuộc tuyến tính kèm lời giải giúp các bạn ôn tập được dễ dàng. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.
Bài viết liên quan: