Trong lý thuyết đồ thị toán rời rạc, ma trận kề ( adjacency matrix ) rất hữu ích trong việc mô phỏng các thuật toán đồ thị như: thuật toán tìm đường đi ngắn nhất và thuật toán tìm cây bao trùm tối thiểu. Bài viết dưới đây, TTnguyen sẽ giới thiệu về lý thuyết, cách biểu diễn đồ thị bằng ma trận kề qua một số bài tập có lời giải. Bắt đầu thôi!
Xem thêm:
- lý thuyết đồ thị toán rời rạc: Đường đi, chu trình, đồ thị liên thông
- Đường đi và chu trình euler
I. Ma trận kề là gì?
Ma trận kề là cách biểu diễn đồ thị G = {V,E} dưới dạng ma trận các giá trị boolean có kích thước bằng với số đỉnh của đồ thị.
Ví dụ ma trận kề:
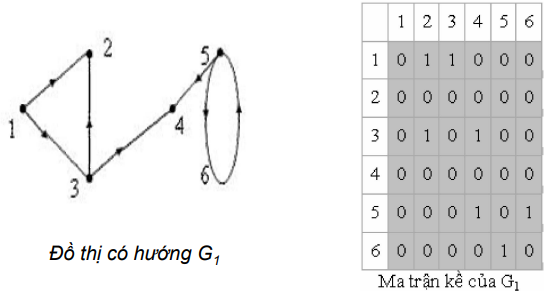
II.Tính chất của ma trận kề
Tính chất của ma trận kề của đồ thị vô hướng:
– Tính đối xứng: a[i,j]=a[j,i], i,j=1,2,. . .,n.
– Tổng các phần từ trên dòng i (cột j) bằng bậc của đỉnh i (đỉnh j).
Tính chất của ma trận kề của đồ thị có hướng:
– Không có tính đối xứng
– Tổng các phần từ trên dòng i bằng bán bậc ra của đỉnh i (deg+(i)) và tổng các phần từ trên cột j bằng bán bậc vào của đỉnh j (deg(-j)).
III. Danh sách kề
Cách biểu diễn đồ thị dưới dạng danh sách kề thường được sử dụng. Trong biểu diễn này, với mỗi đỉnh v của đồ thị chúng ta lưu trữ danh sách các đỉnh kề với nó mà ta ký hiệu là Ke(v), nghĩa là:
Ke(v) = { u∈ V: (u, v)∈E}
Với cách biểu diễn này, mỗi đỉnh i của đồ thị, ta làm tương ứng với một danh sách tất cả các
đỉnh kề với nó và được ký hiệu là List(i). Để biểu diễn List(i), ta có thể dùng các kiểu dữ liệu kiểu tập hợp, mảng hoặc danh sách liên kết.
Ví dụ: Danh sách kề của đồ thị vô hướng được biểu diễn bằng danh sách kề như sau:

Bài viết liên quan
Bài tập ma trận kề
Bài 1: Biểu diễn đồ thị bằng ma trận kề
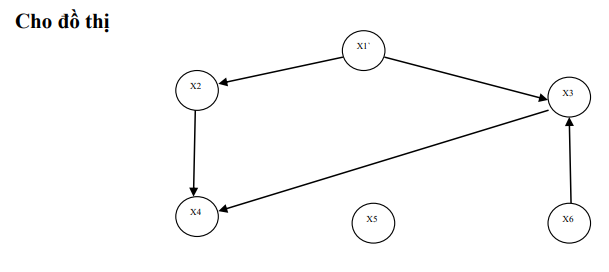
Lời giải

Bài 2: Biểu diễn đồ thị bằng ma trận kề

Lời giải

Bài 3: Biểu diễn đồ thị bằng ma trận kề
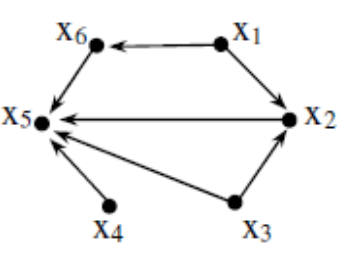

Bài 4: Biểu diễn đồ thị bằng ma trận kề
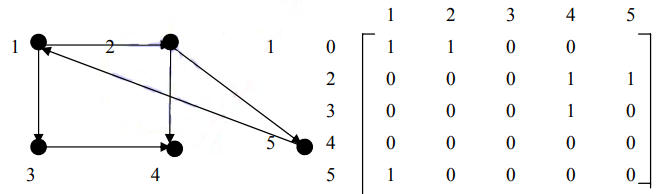
V. Câu hỏi liên quan
Ưu điểm của ma trận kề
Ma trận kề có nhiều ưu điểm:
- Hiệu suất thời gian: Các phép toán cơ bản như thêm cạnh, xóa cạnh và kiểm tra sự tồn tại của cạnh giữa hai đỉnh i và j được thực hiện hiệu quả về mặt thời gian.
- Khả năng xử lý đồ thị dày đặc: Khi đồ thị có nhiều cạnh, ma trận kề thường là lựa chọn tốt vì nó giúp tiết kiệm bộ nhớ và thực hiện các thao tác nhanh chóng.
- Đa dạng về cấu trúc dữ liệu: Ngay cả khi đồ thị và ma trận kề thưa (ít cạnh), ta vẫn có thể sử dụng cấu trúc dữ liệu để biểu diễn ma trận thưa.
- Sử dụng hiệu quả phần cứng: Những tiến bộ trong phần cứng, đặc biệt là GPU, cho phép thực hiện các phép toán trên ma trận kề lớn một cách hiệu quả.
- Hiểu biết về đồ thị: Thực hiện các phép toán trên ma trận kề giúp chúng ta hiểu rõ hơn về cấu trúc và mối quan hệ giữa các đỉnh trong đồ thị.
Nhược điểm của ma trận kề
- Yêu cầu không gian lớn: Ma trận kề cần lưu trữ thông tin về tất cả các cạnh giữa các đỉnh, dẫn đến việc tiêu thụ một lượng lớn bộ nhớ. Kích thước của ma trận là VxV (với V là số lượng đỉnh), dẫn đến một tải nặng về mặt bộ nhớ đặc biệt khi đồ thị lớn.
- Không hiệu quả với đồ thị thưa: Trong hầu hết các trường hợp, số lượng cạnh thực tế trong đồ thị ít hơn nhiều so với số lượng cạnh có thể có trong đồ thị đầy đủ. Điều này làm cho ma trận kề trở nên không hiệu quả về mặt lưu trữ và thao tác, vì nhiều vị trí trong ma trận sẽ không có giá trị.
- Thao tác trên danh sách kề tốn kém: Các thao tác như truy vấn danh sách các cạnh đi vào (inEdges) hoặc cạnh đi ra (outEdges) của một đỉnh cụ thể sẽ rất tốn kém khi sử dụng ma trận kề. Điều này do cần phải duyệt qua toàn bộ hàng hoặc cột tương ứng để trích xuất thông tin.
Ứng dụng của ma trận gần kề
- Tạo bảng định tuyến trong mạng.
- Các bài toán về tìm hướng đi hoặc định vị
Trên đây là một số lý thuyết và bài tập biểu diễn đồ thị bằng ma trận kề có lời giải. Cảm ơn các bạn đã tham khảo trên ttnguyen.net