Bài viết dưới đây sẽ giúp chúng ta tìm hiểu về định nghĩa, phân loại, xét dấu kèm một số dạng bài tập dạng toàn phương có lời giải giúp các bạn ôn tập dễ dàng. Chiến thôi!!!
Xem thêm:
I. Dạng toàn phương toán cao cấp
Dạng toàn phương là một đa thức bậc hai trong các biến \(x_{1}, x_{2},…, x_{n}\). Dạng toàn phương được biểu diễn dưới dạng:
\(f(x) = a_{11} x_1^2 + a_{12} x_1 x_2 + … + a_{1n} x_1 x_n + a_{22} x_2^2 + … + a_{nn} x_n^2\)Trong đó:
-
- các hệ số \(a_{nn}\) là các số thực.
- cách biến \(x_{n}\) là các biến thực.
Có thể viết lại: \(f(x) = x^{T}Mx\).
II. Ma trận dạng toàn phương
Ma trận dạng toàn phương được biểu diễn dưới dạng:
\(x = \begin{pmatrix}x_{1} \\
x_{2} \\
… \\
x_{3}
\end{pmatrix},
A=\begin{pmatrix}
a_{11} & a_{12} & … & a_{1n} \\
a_{21} & a_{22} & … & a_{2n} \\
… & … & … & … \\
a_{n1} & a_{n2} & … & a_{nn}
\end{pmatrix}\)
Ma trận dạng toàn phương A là một ma trận đối xứng.
Có thể bạn quan tâm:
III. Đưa dạng toàn phương về chính tắc
Nếu \(A= \begin{pmatrix}
a_{11} & 0 & 0\\
0 & a_{22} & 0 \\
0 & 0 & a_{nn}
\end{pmatrix}\)
thì dạng chính tắc của dạng toàn phương là \(f(x) = a_{11} x_1^2 + a_{12} x_2^2 + … + a_{nn} x_n^2\)
Đưa dạng toàn phương về dạng chính tắc bằng phương pháp lagrange
Phương pháp Lagrange là sử dụng các phép biến đổi không suy biến đưa dạng toàn phương về dạng chính tắc.
Bước 1: Chọn 1 thừa số khác 0 của hệ số \(x^{2}_{k}\), lập thành 2 nhóm: 1 nhóm gồm tất cả các hệ số chứa \(x_{k}\), nhóm còn lại không chứa \(x_{k}\).
Bước 2: Trong nhóm đầu tiên: lập thành tổng bình phương. Như vậy, ta sẽ được 1 tổng bình phương và 1 dạng toàn phương không chứa \(x_{k}\).
Bước 3: Sử dụng bước 1, 2 cho dạng toàn phương không chứa \(x_{k}\).
Lưu ý: Nếu trong dạng toàn phương ban đầu tất cả các hệ số \(x^{2}_{k}\) đều bằng 0, thì ta chọn thừa số khác 0 của hệ số \(x_{i}x_{j}\). Đổi biến
Đưa dạng toàn phương về dạng chính tắc bằng phương pháp Jacobi
Cho A là ma trận vuông cấp n, A = aij. Coi
\(D_{0} = 1\) \(D_{1} = a11\) \(D_{2} = \begin{vmatrix}a11 & a12\\
a21 & a22
\end{vmatrix}\) \(D_{3} = \begin{vmatrix}
a11 & a12 & a13\\
a21 & a22 & a23 \\
a31 & a32 & a33
\end{vmatrix}\)
F có dạng chuẩn tắc là:
\(G(x1,x2,x3) = \frac{D_{1} (x1)^{2}}{D_{0}} + \frac{D_{2} (x2)^{2}}{D_{1}} + \frac{D_{3} (x3)^{2}}{D_{2}}\)Lưu ý: Chỉ sử dụng phương pháp này với số lượng n nhỏ.
Đưa dạng toàn phương về dạng chính tắc bằng phương pháp trực giao
Bước 1: Viết ma trận A của dạng toàn phương trong cơ sở chính tắc.
Bước 2: Chéo hoá M bởi ma trận trực giao P và ma trận chéo D.
Bước 3: Kết luận: dạng chính tắc cần tìm là \(f(y) = y^{T}Dy\).
Với D là ma trận của dạng toàn phương ban đầu trong cơ sở trực chuẩn từ các cột của ma trận trực giao P.
Phép biến đổi cần tìm x = Py.
Xem thêm:
- tìm cơ sở và số chiều của không gian vecto
- nghiệm tầm thường và nghiệm không tầm thường
IV. Hạng của ma trận toàn phương
Định nghĩa: Cho dạng toàn phương F có ma trận A. Hạng của dạng toàn phương F chính là hạng của ma trận A.
– Nếu A không suy biến <=> \(\left\{ \begin{array}{cl}
\left| A \neq 0\right|\\
r(A) = r(\overline{A})=n
\end{array} \right.\)
=> F cũng không suy biến.
– Nếu A suy biến <=> \(\left\{ \begin{array}{cl}
\left| A = 0\right|\\
r(A) = r(\overline{A})<n
\end{array} \right.\)
V. Phân loại dạng toàn phương (xác định dấu dương, âm)
Dạng toàn phương \(f(x) = X^{T}AX\)
Định nghĩa
- Xác định dương nếu f (X) >0.
- Xác định âm nếu f (X) < 0 (với moi x # 0).
- Nửa xác định dương nếu f (X) ≥ 0.
- Nửa xác định âm nếu f (X) ≤ 0.
- Không xác định dấu f (X). f (Y) < 0.
Giả sử dạng toàn phương đưa về dạng chính tắc được:
- \(f(x) = a_{1} x_1^2 + a_{2} x_2^2 + … + a_{n} x_n^2\)
- Nếu \((\forall k =1,..,n): a_{k}>0\) thì dạng toàn phương xác định dương.
- Nếu \((\forall k =1,..,n): a_{k}<0\) thì dạng toàn phương xác định âm.
- Nếu \((\forall k =1,..,n): a_{k}\ge 0 \text{ và } \exists a_{k} =0 \) thì nửa xác định dương.
- Nếu \((\forall k =1,..,n): a_{k}\le 0 \text{ và } \exists a_{k} =0 \) thì nửa xác định âm.
- Nếu \(\exists a_{1} < 0; a_{2}>0 \) thì dạng toàn phương không xác định dấu.
VI. Dấu hiệu nhận biết tính xác định dấu
– Dấu hiệu 1: giả sử ta dùng các phép biến đổi tuyến tính không suy biến đưa dạng toàn phương ban đầu về dạng chính tắc và xét tính xác định dấu.
– Dấu hiệu 2: Định lý sylvester
Cho dạng toàn phương F có ma trận A. Kí hiệu Dj là các định thức con chính cấp con j của ma trân A. Khi đó:
- Xác định dương khi và chỉ khi định thức con chính cấp j đều dương: \(D_{j}>0\).
- Dạng f(x) xác định âm khi và chỉ khi định thức con chính cấp j đều dương: \(\left\{ \begin{array}{cl}
D_{j} > 0 & , j \text{ chẵn} \\
D_{j} < 0 & , j \text{ lẻ}
\end{array} \right.\).
VII. Bài tập dạng toàn phương
Xem thêm:
- chéo hoá ma trận
- cách tìm ma trận chuyển cơ sở
Bài tập đưa dạng toàn phương về chính tắc



Đưa dạng toàn phương về chính tắc



Tìm dạng chính tắc của dạng toàn phương


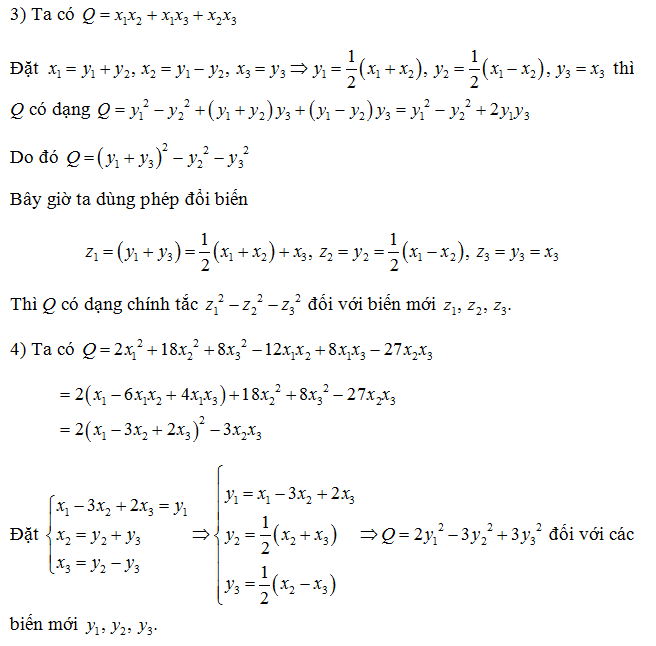
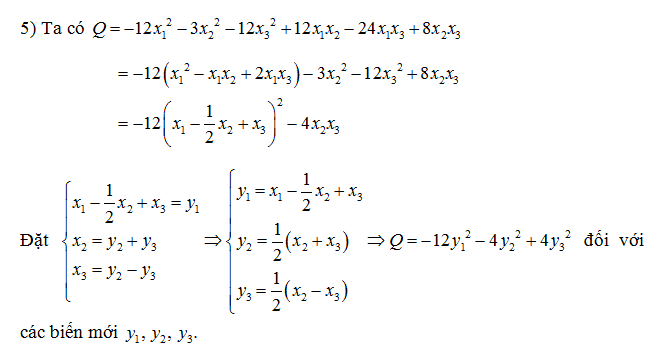
Đưa dạng toàn phương về chính tắc lagrange

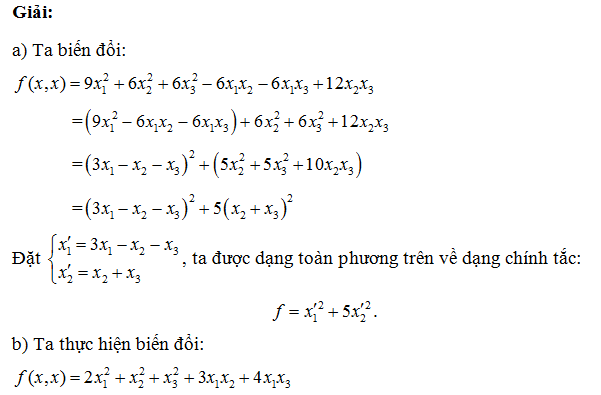
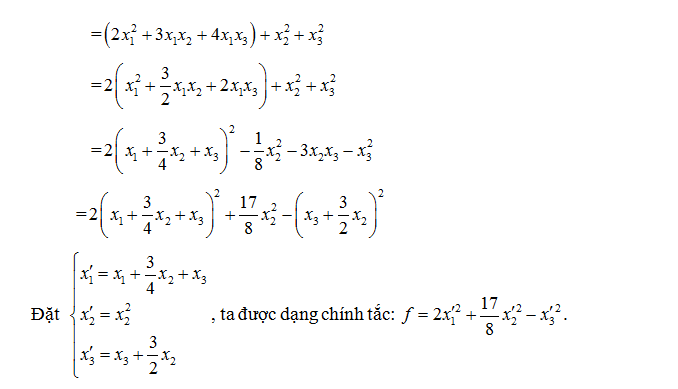
Phương pháp lagrange đưa dạng toàn phương về dạng chính tắc

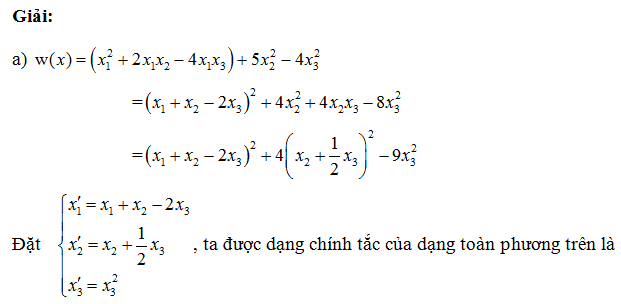
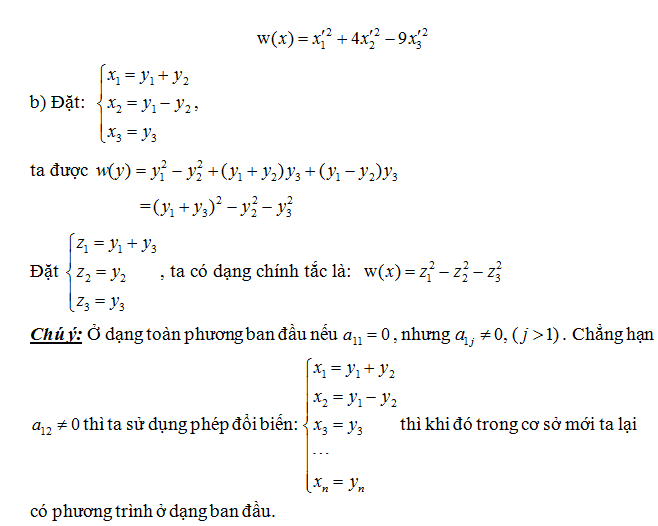
Bài tập xác định dấu của dạng toàn phương
Bài 1: Tìm hạng và xét dấu các dạng toàn phương sau:
\(a) f(x_{1},x_{2}) = -4x_{1}^{2} – 4x_{2}^{2} + 6x_{1}x_{2}\) \(b) f(x_{1},x_{2},x_{3}) = 5x_{1}^{2} + 5x_{2}^{2} + 2x_{3}^{2} – 8x_{1}x_{2} – 4x_{1}x_{3} + 4x_{2}x_{3}\)
Bài 2: Tìm m để dạng toàn phương xác định dương:
\(f(x_{1},x_{2},x_{3}) = 2x_{1}^{2} + (m+1)x_{2}^{2} + 5x_{3}^{2} + 2x_{1}x_{2} + 4x_{1}x_{3} + 4x_{2}x_{3}\)Giải

Bài 3: Tìm m để dạng toàn phương xác định âm:
\(f(x_{1},x_{2},x_{3}) = -2x_{1}^{2} – 5x_{2}^{2} + mx_{3}^{2} – 4x_{1}x_{2} + 4x_{1}x_{3} + 8x_{2}x_{3}\)Giải
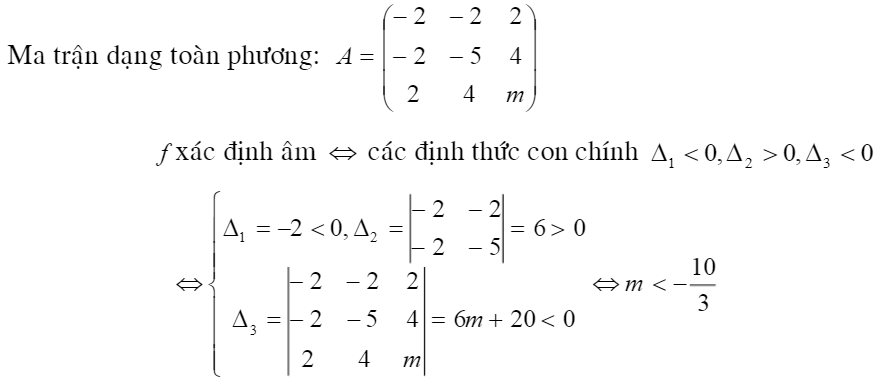
Bài 4: Biện luận hạng và xét dấu dạng toàn phương sau:
\(f(x_{1},x_{2},x_{3}) = 6x_{1}^{2} + x_{2}^{2} + mx_{3}^{2} + 4x_{1}x_{2} + 4x_{1}x_{3} + 2x_{2}x_{3}\)
Ứng dụng dạng toàn phương
Dạng toàn phương là một khái niệm toán học quan trọng với nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
- Toán học: Dạng toàn phương được sử dụng trong đại số và hình học giải tích, hình học đại số, lý thuyết số và tô pô.
- Khoa học máy tính: Dạng toàn phương được sử dụng trong tối ưu hóa, học máy và trí tuệ nhân tạo.
- Khoa học vật lý: Dạng toàn phương được sử dụng trong vật lý hạt nhân, vật lý vật chất ngưng tụ và vật lý thiên văn.
- Khoa học hóa học: Dạng toàn phương được sử dụng trong hóa học tính toán và hóa học vật chất ngưng tụ.
- Khoa học tài chính: Dạng toàn phương được sử dụng trong tài chính định lượng và quản lý rủi ro.
Một số ứng dụng cụ thể của dạng toàn phương bao gồm:
- Giải bài toán tối ưu: Dạng toàn phương có thể được sử dụng để giải các bài toán tối ưu hóa như tìm đường ngắn nhất, tìm diện tích lớn nhất và tìm trọng lượng nhỏ nhất.
- Tìm kiếm các cấu trúc tối ưu: Dạng toàn phương có thể được sử dụng để tìm các cấu trúc tối ưu như cấu trúc phân tử ổn định nhất và cấu trúc vật liệu mạnh nhất.
- Phân tích dữ liệu: Dạng toàn phương có thể được sử dụng để phân tích dữ liệu như phân tích các mối tương quan giữa các biến và phân loại các đối tượng.
- Tạo mô hình dự đoán: Dạng toàn phương có thể được sử dụng để tạo mô hình dự đoán như mô hình dự đoán giá cổ phiếu và mô hình dự đoán thời tiết.
Tài liệu tham khảo dạng toàn phương PDF miễn phí:
Bài viết liên quan: