Bài viết này sẽ tổng hợp tổng hợp kiến thức cơ bản và và một số phương pháp giải bài tập xác suất thống kê chương 2 giúp các bạn ôn tập dễ dàng.
Xem thêm:
- phân phối đều
- phân phối Fisher – snedecor | Cách tra bảng đầy đủ PDF
- phân phối Student | Cách tra bảng giá trị đầy đủ PDF
I. Tổng quan xác suất thống kê chương 1
- Khái niệm cơ bản: biến cố xung khắc, biến cố độc lập, phụ thuộc
- Các quy tắc xác suất:
- Xác suất có điều kiện
- Các định lý xác suất:
- Bài toán lấy ngẫu nhiên có hoàn lại, không hoàn lại hoặc lần lượt, cùng lúc.
- Bài tập về không gian mẫu
- Biểu đồ venn
1. Tổng hợp các công thức cần nhớ
– Công thức cộng xác suất:
P(A∪B) = P(A) + P(B) – P(A∩B)– Quy tắc nhân xác suất:
P(A∩B) = P(A)P(B/A); Khi A xảy ra trước B.
P(A∩B) = P(B)P(A/B); Khi B xảy ra trước A.
– Công thức Bayes:
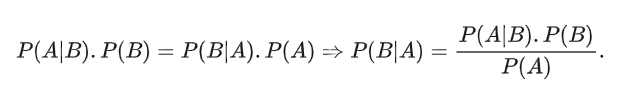
– Công thức xác suất đầy đủ:
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3)
2. Các dạng bài tập cơ bản và lời giải chương 1
2.1. Dạng Bài tập xác suất phương pháp cổ điển
Bài 1: Một người gọi điện thoại cho bạn nhưng quên mất 2 chữ số cuối của số điện thoại chỉ nhớ rằng 2 chữ số này là khác nhau. Tính xác suất để người đó bấm ngẫu nhiên gọi đúng số hiệu điện thoại của bạn.
Giải
Gọi 2 số cuối là ab, là số điện thoại nên có đủ các chữ số từ 0 đến 9
Ta có a có 10 cách chọn, b khác a nên có 9 cách chọn. Vậy không gian mẫu có 9.10= 90 phần tử.
Vậy xác xuất gọi một lần dúng là 1/90
Bài 2: Trong một hộp có 15 tấm thẻ như nhau được đánh số từ số 1 đến số 15. Rút ngẫu nhiên lần lượt ra 2 tấm thẻ rồi đặt theo thứ tự từ trái qua phải. Tính xác suất để:
a) Rút được hai thẻ lập nên một số có hai chữ số.
b) Rút được hai tấm thẻ lập nên một số chia hết cho 5.
Giải
Tổng số cách rút hai tấm thẻ từ 15 tấm là \mathrm{C}_{15}^{2}
a. Để rút được hai thẻ và lập nên một số có hai chữ số, có thể chọn các tấm thẻ từ số 1 đến 9. Số cách chọn là \mathrm{C}_{9}^{2}.
Vậy xác suất cần tính là: \frac{\mathrm{C}_{9}^{2}}{\mathrm{C}_{15}^{2}}
b. Để rút được hai tấm thẻ và lập nên một số chia hết cho 5, có thể chọn các tấm thẻ từ số 5, 10, hoặc 15. Số cách chọn là \mathrm{C}_{3}^{2}.
Vậy xác suất cần tính là: \frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{15}^{2}}
2.2. DẠng Bài tập công thức xác suất có điều kiện
Bài 3: Có một lô hàng máy tính, trong đó mỗi máy tính có hoặc không có ổ cứng di động và có hoặc không có ổ CD RW, số liệu được cho trong bảng sau:
Gọi A là biến cố máy tính có ổ cứng di động và b là biến cố máy tính có ổ CD RW. Chọn ngẫu nhiên một máy tính trong lô hàng đó, tính xác suất:
a) P(A); b) P(B);
c) P(A ∩ B); d) P(A ∪ B);
e) P(A/B); f) P(B/A);
Giải
Ta có tổng số máy tính: 514 + 68 + 112 + 246 = 940 máy tính.
a) P(A)
P(A) là xác suất để máy tính có ổ cứng di động.
Do đó, P(A) bằng 514+112/940, xấp xỉ bằng 0,665.
b) P(B)
P(B) là xác suất để máy tính có ổ CD RW.
Do đó, P(B) bằng 514+68/940, xấp xỉ bằng 0,61.
c) P(A ∩ B)
P(A ∩ B) là xác suất để máy tính có cả ổ cứng di động và ổ CD RW.
Do đó, P(A ∩ B) bằng 514/940, xấp xỉ bằng 0,546.
d) P(A ∪ B)
P(A ∪ B) là xác suất để máy tính có ít nhất một trong hai loại ổ.
Do đó, P(AUB) bằng 514+112+68/940, xấp xỉ bằng 0,738.
e) P(A/B)
P(A/B) là xác suất để máy tính có ổ cứng di động, biết rằng máy tính có ổ CD RW.
Ta có P(A/B) = P(A ∩ B)/P(B) = 0,546/0,61.
f) P(B/A)
P(B/A) là xác suất để máy tính có ổ CD RW, biết rằng máy tính có ổ cứng di động.
Ta có P(B/A) = P(A ∩ B)/P(A) = 0,546/0,665.
2.3. DẠng Bài tập công thức nhân xác suất
Bài 8: Hoạt động của một hệ thống thông tin gồm 3 giai đoạn: Mã hóa, truyền tin và giải mã. Một tin nhắn có xác suất bị lỗi trong giai đoạn mã hóa là 0,5%; trong giai đoạn truyền tin là 1% và trong giai đoạn giải mã là 0,1%. Giả sử các lỗi xảy ra ở các giai đoạn là độc lập.
a. Xác suất để một tin nhắn không bị lỗi là bao nhiêu?
b. Xác suất để một tin nhắn bị lỗi ở giai đoạn mã hóa hoặc giai đoạn giải mã là bao nhiêu?
Giải
a)
Gọi A là biến cố”tin nhắn không bị lỗi”
A1 là biến cố “tin nhắn bị lỗi ở giai đoạn mã hoá”
A2 là biến cố “tin nhắn bị lỗi ở giai đoạn truyền tin”
A3 là biến cố “tin nhắn bị lỗi ở giai đoạn giải mã”
A=\overline{A1}.\overline{A2}.\overline{A3}
=>P(A)=P(\overline{A1}).P(\overline{A2}).P(\overline{A3})
=0,95.0,99.0,99=0,984
b)Gọi B là biến cố “tin nhắn bị lỗi ở giai đoạn mã hoá hoặc giai đoạn giải mã”
B= A1∪A3=> P(B)=P(A1∪A3)= P(A1)+P(A3)-P(A1A3)= 0,5%+0,1%-(0,5%.0,1%)=0,00599
Bài 9: Một phòng có 3 máy tính hoạt động độc lập. Xác suất hỏng trong một tháng của mỗi máy tương ứng là 0,1; 0,2; 0,3. Tính xác suất:
a. Cả ba máy hỏng trong tháng.
b. Có một máy hỏng trong tháng.
c. Có hai máy hỏng trong tháng.
d. Có ít nhất một máy hỏng trong tháng.
e. Máy thứ ba bị hỏng. Biết rằng trong tháng có 2 máy bị hỏng.
Giải
a)Gọi A là biến cố “cả 3 máy hỏng trong tháng”
P(A)=0,1.0,2.0,3=0,006
b)Gọi B là biến cố “có một máy hỏng trong tháng”
Có đúng 1 máy hỏng=>Xảy ra 3 TH:
+) TH1: Máy 1 hỏng, máy 2,3 bình thường
=>P1=0,1.(1-0,2).(1-0,3)=0,056
+) TH2: Máy 1,3 bình thường, máy 2 hỏng
=>P2=(1-0,1).0,2.(1-0,3)=0,126
+) TH3: Máy 1,2 bình thường, máy 3 hỏng
=>P3=(1-0,1).(1-0,2).0,3=0,216
=>P(B)=P1+P2+P3=0,398
c) Gọi C là biến cố “có 2 máy hỏng trong tháng”
Có đúng 2 máy hỏng=>Xảy ra 3 TH:
+) TH1: Máy 1 hoạt động bình thường, máy 2,3 hỏng
=>P1(C)=(1-0,1).0,2.0,3=0,054
+) TH2: Máy 1,3 hỏng, máy 2 bình thường
=>P2(C)=0,1.(1-0,2).0,3=0,024
+) TH3: Máy 1,2 hỏng, máy 3 bình thường
=>P3(C)=0,1.0,2.(1-0,3)=0,014
=>P(C)=P1(C)+P2(C)+P3(C)=0,092
d) Gọi \overline{D} là biến cố”không có máy nào hỏng”,D là biến cố có ít nhất một máy bị hỏng
P(D)=1-P(\overline{D})
= 1 – [(1-0,1).(1-0,2).(1-0,3)]
=0,496
e) P(E)= P(P1(C)∪P2(C)|P(C))
=\frac{P1(C)∪P2(C)}{P(C)} =\frac{0,054+0,024}{0,092} =0,852.4. Dạng Bài tập công thức bernoulli
Bài 13: Một tín hiệu thông tin được phát 3 lần một cách độc lập với xác suất thu được mỗi lần bằng 0,4.
a. Tính xác suất để nhận được tín hiệu thông tin đó.
b. Nếu muốn xác suất thu được tín hiệu thông tin đó lên tới 0,9 thì cần phát bao nhiêu lần?
Giải
Xác suất để không nhận được tín hiệu: \bar{P}=\mathrm{C}_{3}^{3}(1-0,4)^{3}=0,216
a. Tính xác suất để nhận được tín hiệu thông tin đó là: 1-\bar{P} = 1-0,6^3 = 0.784
b. Gọi số lần phát thông tin là x
Do xác suất thu được tín hiệu ít nhất 1 lần là 0,9 nên:
1-P(0)\ge 9 => P(0)\le 0,1 \\ (1-0,4)^{x} \le 0,1 \\ x\ge log_{0,6}0,1 \\ =>x_{min}=5 (\text{x nguyên dương})2.5. DẠng Bài tập công thức bayes và xác suất đầy đủ
Bài 14: Một người có 3 chỗ ưa thích như nhau để câu cá. Xác suất câu được cá ở mỗi chỗ lần lượt là 0,7; 0,8; 0,9. Biết rằng mỗi chỗ người đó thả câu 3 lần thì chỉ có một lần câu được cá. Người đó đã câu được một con cá. Tính xác suất để con cá câu được đó ở chỗ thứ nhất.
Giải
Gọi A là sự kiện câu được cá ở chỗ thứ 1, B là sự kiện câu được 1 con cá.
Theo đề bài, ta biết rằng người đó chọn ngẫu nhiên 1 chỗ rồi thả câu 3 lần và chỉ câu được 1 con cá. Ta cần tìm xác suất P(A|B), tức là xác suất câu được cá ở chỗ thứ 1 khi biết đã câu được 1 con cá.
Theo công thức Bayes, ta có:
P(B|A) = \frac{P(A|B).P(B)}{P(A)}Trong đó:
- P(B|A) là xác suất câu được 1 con cá khi đã biết câu ở chỗ thứ 1 là A. Vì xác suất câu được cá ở chỗ thứ 1 là 0.8, nên P(B|A) = 0.8.
- P(A) là xác suất câu được cá ở chỗ thứ 1. Vì có 3 chỗ ưa thích như nhau, nên xác suất câu được cá ở chỗ thứ 1 là 1/3.
- P(B) là xác suất câu được 1 con cá. Ta có thể tính xác suất này bằng cách sử dụng định lý xác suất toàn phần:
Trong đó:
- P(B|\bar{A})là xác suất câu được 1 con cá khi không câu ở chỗ thứ 1 là A. Vì xác suất câu được cá ở chỗ thứ 2 và chỗ thứ 3 lần lượt là 0.9 và 0.7, nên P(B|\bar{A})= 0.9 * 0.7.
- P(\bar{A})là xác suất không câu được cá ở chỗ thứ 1. Vì có 3 chỗ ưa thích như nhau, nên xác suất không câu được cá ở chỗ thứ 1 là 2/3.
Thay các giá trị vào công thức Bayes, ta có:
0,8 = \frac{P(A|B).0,42}{\frac{1}3{}}Vậy Xác suất con cá câu được ở chỗ thứ 1 là: 0,112
Bài 15: Một chiếc máy bay có thể xuất hiện không phận của điểm A với xác suất là 2/3 hoặc không phận của điểm B với xác suất là 1/3. Giá sử có 3 phương án bó trí 4 khẩu pháo để hạ máy bay như sau:
Phương án 1: 3 khẩu đặt ở điểm A và 1 khẩu đặt ở điểm B.
Phương án 2: 2 khấu đặt ở điểm A và 2 khẩu đặt ở điểm B.
Phương án 3: 1 khẩu đặtở điểm A và 3 khẩu đặt ở điểm B.
Biết rằng xác suất bắn trúng (hạ máy bay) của mỗi khẩu bằng 0,7 và các khẩu pháo bắn độc lập với nhau. Nên chọn phương án nào? Tại sao?
Giải
Phương án 1: 3 khẩu đặt tại A và 1 khẩu đặt tại B Nếu có 3 khẩu đặt tại A thì để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại A bắn trúng máy bay:
1-0,3^3=0,973(tính theo biến cố đối của biến cố: không có khẩu nào bắn trúng)
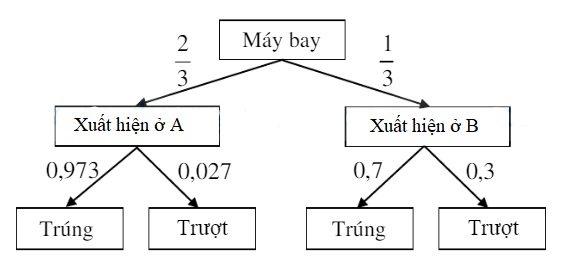
=> Xác suất để máy bay rơi trong phương án I:
P_1=\frac{2}{3}.0,973+\frac{1}{3}.0,7=0,882 (1)
Phương án 2: 2 khẩu đặt tại 4 và 2 khẩu đặt tại B Nếu có 2 khẩu đặt tại A thì để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại A bắn trúng máy bay:
1-0,3^2=0,91Tương tự, xác suất để ít nhất một khẩu tại B bắn trúng máy bay:
1-0,3^2=0,91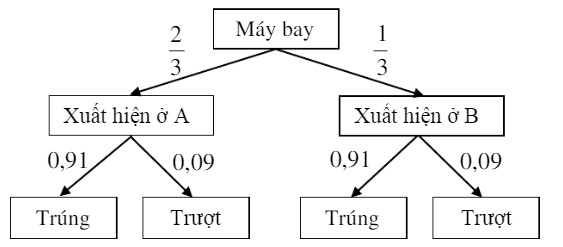
=> Xác suất để máy bay rơi trong phương án II:
P_2=\frac{2}{3}.0,91+\frac{1}{3}.0,91=0,91 (2)
Phương án 3: 1 khẩu đặt tại A và 3 khẩu đặt tại B com Nếu có 3 khẩu đặt tại B thì để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại B bắn trúng máy bay:
1-0,3^3=0,973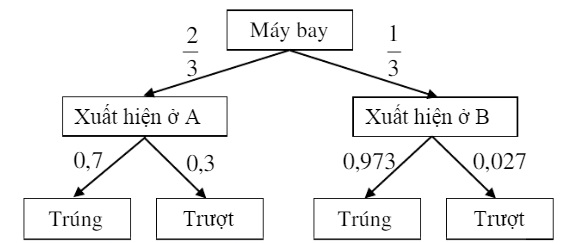
=> Xác suất để máy bay rơi trong phương án I:
P_3=\frac{2}{3}.0,7+\frac{1}{3}.0,973=0,791 (3)
Từ (1), (2) và (3) suy ra: phương án 2 có xác suất bắn trúng máy bay cao nhất. Chọn phương án 2 để đạt hiệu quả tốt nhất.
2.6. Tổng hợp một số bài tập chương 1
Bài 4: Một hệ thống bảo mật máy tính sử dụng Password bao gồm 7 ký tự, trong đó mỗi ký tự là một trong 26 chữ cái (a-z) hoặc một trong 10 chữ số (0-9). Bạn đang sử dụng một Pasword trong máy tính. Gọi A là tập con Pasword bắt đầu là một nguyên âm (a, e, i,o ,u). Gọi B là tập con Pasword kết thúc với các số chẵn (0, 2, 4, 6 hoặc 8).
a. Giả sử một Hacker mò Pasword một cách ngẫu nhiên. Tính xác suất để Password của bạn bị lộ.
b. Giả sử Hacker biết Password của bạn là biến cố A và chọn ngẫu nhiên một Password từ tập đó. Tính xác suất để Password của bạn bị lộ.
c. Giả sử Hacker biết Password của bạn là biến cố A∩ B và chọn ngẫu nhiên một Password từ tập đó. Tính xác suất để Password của bạn bị lộ.
Giải
a) Xác suất để Password bị lộ:
P(A)=\frac{1}{36^7}b) Xác suất để Pass bị lộ:
P(B)=\frac{1}{5.36^6}c) Xác suất để Password bị lộ:
P(C)=\frac{1}{5.5.36^5}Bài 5: Có 10 người trong đó có 2 người trùng tên. Tính xác suất khi sắp xếp ngẫu nhiên để 2 người trùng tên đứng cạnh nhau nếu:
a)Họ xếp thành hàng ngang
b)Họ xếp thành vòng tròn
c)Cũng các câu hỏi trên nhưng có m người trong đó có k người trùng tên(k<n)
Giải
Không gian mẫu n= P_{10}=10!
Gọi A là biến cố “xếp 10 người thành hàng ngang sao cho 2 người trùng tên đứng cạnh nhau”
P(A) = \frac{9!.2!}{10!}
Gọi B là biến cố “xếp 10 người thành vòng tròn sao cho 2 người trùng tên đứng cạnh nhau”
P(B) = \frac{8!.2!}{9!}
Xếp thành hàng ngang:
P(A) = \frac{(k-s+1)!.s!}{k!}
Xếp thành vòng tròn
P(A) = \frac{(k-s+1+1)!.s!}{(k-1)!}
Bài 6: Rút ngẫu nhiên 2 quân bài từ bộ bài 52 quân. Tính xác suất:
a)Cả 2 quân đều là Át
b)Có một quân Át trong 2 quân
c)Có ít nhất một quân Át
Giải
Không gian mẫu: C_{52}^{2}
a Gọi A là biến cố “cả 2 quân đều là Át”
P(A) = \frac{C_{4}^{2}}{C_{52}^{2}}
b. Gọi B là biến cố “có một quân Át trong 2 quân”
P(B) = \frac{C_{4}^{1}.C_{48}^{1}}{C_{52}^{2}}
c. Gọi C ngang là biến cố 2 quân không phải quân Át
P(C) = \frac{C_{52}^{2}-C_{48}^{2}}{C_{52}^{2}}
Bài 7: Ngân hàng đề thi môn học có 30 câu. Một đề thi gồm 2 câu được chọn ngẫu nhiên trong đề cương. Một sinh viên chỉ học thuộc 12 câu. Tính xác suất để sinh viên đó thi đỗ. Biết rằng muốn thi đỗ sinh viên phải thuộc ít nhất một câu trong đề thi.
Giải
Tổng số cách chọn 2 câu từ tất cả các câu trong đề là \mathrm{C}_{30}^{2}
Xác suất sinh viên không học thuộc bài là: \frac{\mathrm{C}_{18}^{2}}{\mathrm{C}_{30}^{2}}
Vậy xác suất sinh viên đỗ là: 1-\frac{\mathrm{C}_{18}^{2}}{\mathrm{C}_{30}^{2}}
Bài 10: Một hệ thống kỹ thuật có 5 bộ phận được kết nối theo 2 phương thức và xác suất làm việc tốt của mỗi bộ phận được cho như sau:
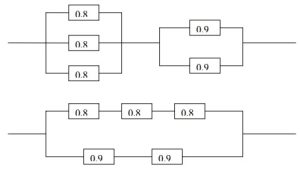
Hãy kết luận xem phương thức nào có độ tin cậy (xác suất làm việc tốt) cao hơn cho hệ thống kỹ thuật? Tại sao?
Giải
Gọi A là hệ thống kỹ thuật được thiết kế theo phương pháp 1
Gọi B là hệ thống kỹ thuật được thiết kế theo phương pháp 2
Gọi A1 là cụm linh kiện 1 (gồm 3 linh kiện mắc //) hoạt động tốt
Gọi A2 là cụm linh kiện 2 (gồm 2 linh kiện mắc //) hoạt động tốt
=> P(A)=P(A1).P(A2)
Gọi E1 là linh kiện 1 hoạt động tốt
Gọi E2 là linh kiện 2 hoạt động tốt
Gọi E3 là linh kiện 3 hoạt động tốt
\overline{A1}= \overline{E1}.\overline{E2}.\overline{E3} P(\overline{A1})= P(\overline{E1}).P(\overline{E2}).P(\overline{E3})=0,2^3 P(A1)=1-P(\overline{A1})=1-0,2^3=0,992 P(A2)=1-P(\overline{A2})=1-0,1^3=0,999=> P(A)=0,992.0,999=0,991008
Gọi F1 là cụm linh kiện 1 (gồm 3 linh kiện mắc nối tiếp) hoạt động tốt
Gọi F2 là cụm linh kiện 2 (gồm 2 linh kiện mắc nối tiếp) hoạt động tốt
P(B)=P(F1).P(F2)=0,8.0,9=0,72
Vậy phương thức 1 mắc song song có xác suất làm việc tốt hơn
Bài 11: Gieo đồng thời 2 con xúc xắc đều đặn và đồng chất. Tính xác suất để nhận được hai mặt:
a. Có tổng số chấm bằng 7
b. Có tổng số chấm nhỏ hơn 8
c. Có số chấm như nhau
d. Có ít nhất một mặt 6 chấm
Giải
Không gian mẫu n=6.6=36
Gọi A là biến cố”tổng số chấm bằng 7”
A={(1;6),(2;5),(3;4),(4;3),(5;2),(6;1)}
P(A) = \frac{m(A)}{n}= \frac{6}{36} = \frac{1}{6}
Gọi B là biến cố “tổng số chấm nhỏ hơn 8”
B={(1;1),(1;2),(1;3),(1;4),(1;5),(1;6),(2;1),(2;2),(2;3),(2;4),(2;5),(3;1),(3;2),(3;3),(3;4),(4;1),(4;2),(4;3),(5;1),(5;2),(6;1)}
=> P(B) = \frac{m(B)}{n}= \frac{21}{36}
Gọi C là biến cố “có tổng số chấm như nhau”
C={(1;1),(2;2),(3;3),(4;4),(5;5),(6;6)}
P(C) = \frac{m(C)}{n}= \frac{6}{36} = \frac{1}{6}
Gọi D là biến cố “có ít nhất một mặt 6 chấm”
D={(6;1),(6;2),(6;3),(6;4),(6;5),(6;6),(1;6),(2;6),(3;6),(4;6),(5;6)}
P(D) = \frac{m(D)}{n}= \frac{11}{36}
Bài 12: Một hệ thống bảo mật máy tính sử dụng Password bao gồm 7 ký tự, trong đó mỗi ký tự là một trong 26 chữ cái (a-z) hoặc một trong 10 chữ số (0-9).
a. Có bao nhiêu Pasword có thể lập được theo yêu cầu trên
b. Tính xác suất để chọn ngẫu nhiên một Password có đúng 6 chữ cái và một chữ số.
c. Xác suất để chọn ngẫu nhiên một Password có 2 chữ số đứng trước và 5 chữ cái đứng sau.
Giải
Số password có thể lập được chính là chỉnh hợp lặp chập 7 của 36 phần tử
A_{36}^{7}= {36}^{7}
Chọn 6 chữ cái trong 26 chữ cái C_{26}^{6}
Chọn 1 chữ số trong 10 chữ số C_{10}^{1}
P(B)= C_{26}^{6}. C_{10}^{1}
Chọn 2 chữ số đứng trước: A_{10}^{2}
Chọn 5 chữ cái đứng sau: A_{26}^{5}
P(C) = A_{26}^{5} . A_{10}^{2}
II. Tổng quan kiến thức chương 2 xác suất thống kê
1. Tổng hợp kiến thức xác suất thống kê chương 2
- Biến ngẫu nhiên và phân loại biến ngẫu nhiên
- Biến ngẫu nhiên hai chiều
- Biến ngẫu nhiên rời rạc một chiều
- Bảng phân phối xác suất của biến ngẫu nhiên rời rạc
| X(x_i) | x_1 | x_2 | x_3 | x_4 | x_5 | x_n |
| P(x_i) | P(x_1) | P(x_2) | P(x_3) | P(x_4) | P(x_5) | P(x_n) |
-
- Phân phối nhị thức
Bảng phân phối nhị thức

Công thức phân phối nhị thức dành cho bất kỳ biến ngẫu nhiên X, được cho bởi:
P(X=k)=C^{k}_{n}p^{k}(1-p)^{n-k}
Với:
-
-
-
-
- n: số lần phép thử
- k=0,1,2,…,n
- p: xác suất thành công của phép thử
-
-
-
-
- Phân phối Poisson
Biến ngẫu nhiên rời rạc X được gọi là có phân phối Poisson với tham số λ, ký hiệu là X ∼ P (λ ), nếu X nhận các giá trị có thể có là các số nguyên không âm: 0, 1, 2, … , n và các suất tương ứng được tính theo công thức xấp xỉ Poisson.
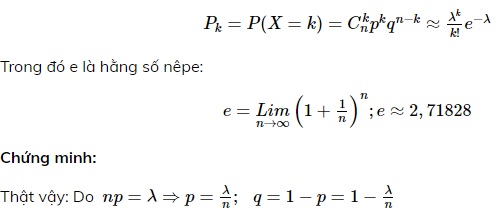
2. Các dạng bài tập xác suất thống kê chương 2 có lời giải
2.1. Dạng bài tập về phân phối xác suất
Bài 1: Có 2 nhóm sinh viên. Nhóm thứ nhất có 4 nam và 6 nữ. Nhóm thứ 2 có 3 nam và 7 nữ.
a. Từ mỗi nhóm chọn ngẫu nhiên ra 1 sinh viên. Gọi X là số sinh viên nam trong số sinh viên chọn ra
i.Lập bảng phân phối của X
ii. Tính xác suất để trong số sinh viên chọn ra có ít nhất một nam
b. Từ nhóm thứ nhất chọn ngẫu nhiên ra 2 sinh viên và từ nhóm thứ hai chọn ngẫu nhiên ra 1 sinh viên. Gọi X là số sinh viên nữ trong số sinh viên chọn ra. Hãy lập bảng phân phối xác suất của X.
Giải
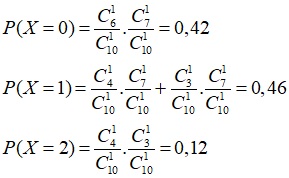
i. Bảng phân phối của X
| X | 0 | 1 | 2 |
| P | 0,42 | 0,46 | 0,12 |
Xác suất để trong số sinh viên chọn ra có ít nhất một nam là:
P(A)=0,46+0,12=0,58
b.
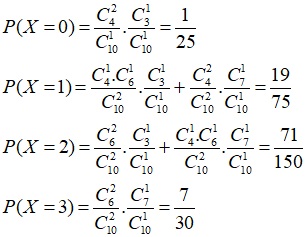
Bảng phân phối xác suất là:
| X | 0 | 1 | 2 | 3 |
| P | 1/25 | 19/75 | 71/150 | 7/30 |
2.2. Dạng bài tập về phân phối nhị thức
Bài 3: Một lô hàng có 8 sản phẩm loai I và 2 sản phẩm loại II. Lấy ngẫu nhiên lần lượt ra 5 sản phẩm theo phương thức hoàn lại. Gọi X là số sản phẩm loại II trong 5 sản phẩm lấy ra.
a) X có phân phối gì?
b) Tính kỳ vọng và phương sai của X.
c) Tính số sản phẩm loại II trung bình trong số sản phẩm lấy ra và tính khả năng để xảy ra điều đó.
d) Nếu lấy lần lượt ra 64 sản phẩm từ lô hàng đó (vẫn lấy theo phương thức hoàn lại) thì trung bình lấy được bao nhiêu sản phẩm loại II? Số sản phẩm loại II có khả năng xảy ra nhất là bao nhiêu?
Giải
a. X có phân phối nhị thức: n = 5; p = 0,2
b. E (X) = n.p = 5.0,2 = 1; V (X) = 5.0,2.0,8 = 0,8
c.
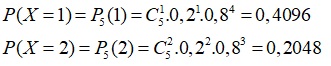
d.Gọi Y là số sản phẩm loại 2 có trong 64 sản phẩm lấy ra Y có phân phối nhị thức n = 64; p = 0,2
E (Y) = 64.0,2 = 12,8.
Như vậy trong 64 sản phẩm thì có 13 sản phẩm loại 2.
Số sản phẩm loại 2 có nhiều khả năng là Y mod của Y
64.0,2-0 , 8 <= Ymod <= 64.0,2 + 0,2
12 <= Ymod <= 13
Ymod <= 12: 13
2.3. Dạng bài tập về phân phối Poission
Các cuộc gọi đến một tổng đài bưu điện trong một phút xuất hiện ngẫu nhiên độc lập có phân phối Poisson với 2 cuộc gọi trung bình trong 1 phút.
a) Trong khoảng thời gian 2 phút thì trung bình có bao nhiêu cuộc gọi đến tổng đài đó? Trong khoảng thời gian 30 giây thi trung bình có bao nhiêu cuộc gọi?
b) Tính xác suất để trong 30 giây không có cuộc gọi nào đến tổng đài.
c) Tính xác suất để trong 2 phút có 3 cuộc gọi đến tổng đài.
Giải
a) Gọi X là số cuộc gọi đến tổng đài trong 1 phút. Theo giả thiết X có phân phối Poisson với trung bình λ = 2 ( X~ P(2)).
Goi Y là số cuộc gọi đến tổng đài trong 2 phút, Y có phân phối Poisson với trung bình λ1= 4 cuộc gọi (Y~ P(4)).
Gọi Z là số cuộc gọi đến tổng đài trong 30 giây, Z có phân phối Poisson với trung bình λ2 = 1 (Z ~ P(1)).
b) Cần tính: P(Z=0)\approx P_0 = \frac{\lambda_2^0}{0!}e^{-\lambda_2}=\frac{1^0}{0!}e^{-1}\approx 0,359
c) Cần tính: P(Y=3)\approx P_3 = \frac{\lambda_1^3}{3!}e^{-\lambda_1}=\frac{4^3}{3!}e^{-4}\approx 0,178
Tài liệu xác suất thống kê chương 2 PDF:
Trên đây là các dạng bài tập xác suất thống kê chương 2. Cảm ơn bạn đã tham khảo trên ttnguyen.net.
Bài viết liên quan:
- phân phối mũ – Công thức tính và bài tập có lời giải
- phân phối siêu bội – Công thức và bài tập có lời giải
- bảng phân phối chi bình phương, Gamma | Cách tra và bài tập