Dưới đây TTnguyen xin gửi tới bạn một số bài tập biến ngẫu nhiên liên tục trong môn xác suất thống kê. Chúc các bạn học tập tốt!
Xem thêm:
Sơ Đồ Venn trong xác suất thống kê
Bài tập xác suất có điều kiện có lời giải chi tiết
Bài tập công thức xác suất đầy đủ
1. Biến ngẫu nhiên liên tục và các khái niệm liên quan
1.1. Biến ngẫu nhiên liên tục là gì?
Biến ngẫu nhiên liên tục là biến ngẫu nhiên mà các giá trị của nó lấp đầy một khoảng nào đó trên trục số. Nghĩa là miền giá trị của nó là một khoảng (hữu hạn hoặc vô hạn) của các số thực.
Ví dụ:
- Thời gian chờ xe buýt trong khoảng từ 0 đến 60 phút.
- Gọi Z là thời gian truy cập mạng Internet của một người trong một ngày. Z là biến ngẫu nhiên liên tục: Z∈ [0 ; 24].
1.2. Biến định lượng liên tục là gì?
Biến định lượng liên tục là loại biến số có thể nhận bất kỳ giá trị nào trong một khoảng nhất định trên trục số thực. Chúng thường dùng để đo lường và có khả năng biểu thị các giá trị lẻ hoặc thập phân, giúp phân tích sâu sắc hơn trong thống kê.
Ví dụ về biến định lượng liên tục:
- Trọng lượng của một quả bí ngô (có thể là 2.53 kg hoặc 5.76 kg).
- Chiều cao của một người (1.75 m, 1.805 m, v.v.).
2. Phân phối xác suất của biến ngẫu nhiên liên tục
2.1. Hàm mật độ xác suất của biến ngẫu nhiên liên tục
Cho biến ngẫu nhiên liên tục X, hàm mật độ của biến ngẫu nhiên liên tục ký hiệu là f(x) là hàm thỏa mãn:

2.2. Tính chất

2.3. Hàm phân phối tích luỹ – hàm phân phối xác suất của biến ngẫu nhiên liên tục
Hàm phân phối tích lũy (hàm phân phối xác suất ) của biến ngẫu nhiên liên tục X, ký hiệu là F(x), là hàm sau:
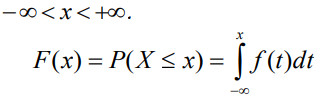
2.4. Các tính xác suất của biến ngẫu nhiên liên tục
Xác suất được tính bằng tích phân của hàm mật độ xác suất trên khoảng xác định: P(a\le X\le b) = \int_{a}^{b}f(x)dx
3. Các đặc trưng của biến ngẫu nhiên tục
3.1. Kỳ vọng
Giả sử f(x) là hàm mật độ xác suất của biến ngẫu nhiên liên tục X. Kỳ vọng (giá trị trung bình) của X , ký hiệu là μ hay E(X), được định nghĩa:
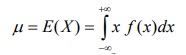
3.2 Phương sai và độ lệch chuẩn

4. Ví dụ và bài tập về biến ngẫu nhiên liên tục
4.1. Bài tập biến ngẫu nhiên liên tục x có hàm mật độ
Bài 1: Nhu cầu hàng năm về loại hàng hóa A là biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau: (đơn vị: ngàn sản phẩm)

a) Tìm hệ số k.
b) Tìm nhu cầu trung bình hàng năm về loại hàng hóa đó.
c) Tìm xác suất để nhu cầu hàng năm về loại hàng hóa đó không vượt quá 12.
Giải
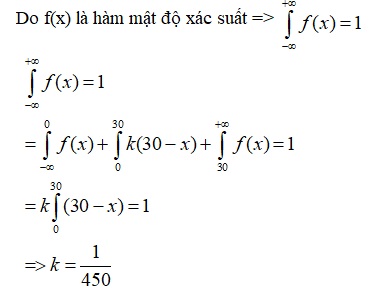
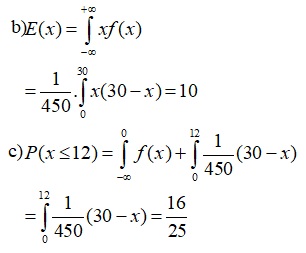
Bài 2: Thời gian xếp hàng chờ mua hàng của khách hàng là biến ngẫu nhiên liên tục với hàm phân phối tích lũy được cho như sau: (đơn vị là phút)

a) Tìm hệ số k.
b) Tìm thời gian xếp hàng trung bình.
c) Tính xác suất để có 3 người xếp hàng thì có không quá 2 người
phải chờ hơn 0,5 phút.
Giải

Bài 3: Một bến xe buýt cứ 10 phút có 1 chuyến xe đến bến tại một thời điểm nào đó. Tính xác suất 1 hành khách xuất hiện ở bến xe không sớm hơn 1 phút sau chuyến ô tô trước chuyển bánh; không muộn hơn 2 phút khi chuyến ô tô tiếp theo khởi hành.
Giải

4.2. Bài tập biến ngẫu nhiên liên tục có phân phối chuẩn
Bài 4: Thời gian sạc pin của laptop trong điều kiện bình thường là biến ngẫu nhiên có phân phối chuẩn với thời gian trung bình là 260 phút và độ lệch tiêu chuẩn là 50 phút.
a) Tính tỷ lệ laptop có thời gian sạc pin trên 4 giờ.
b) Thời gian sạc pin cần thiết là bao nhiêu để 95% laptop có thời gian sạc pin không vượt quá thời gian đó.
Giải

4.3. Bài tập về các đặc trưng của biến ngẫu nhiên liên tục

Giải

Bài 6: Thời gian đi từ nhà đến trường của một sinh viên A là biến ngẫu nhiên có phân phối chuẩn. Biết rằng có 65% số ngày sinh viên A đến trường mất hơn 20 phút. 8% số ngày sinh viên A đến trường mất hơn 30 phút.
a) Tình thời gian trung bình và độ lệch chuẩn của thời gian đi từ nhà đến trường của sinh viên A.
b) Nếu sinh viên A xuất phát từ nhà trước giờ học 25 phút thì tỷ lệ ngày đi học muộn là bao nhiêu?
Giải
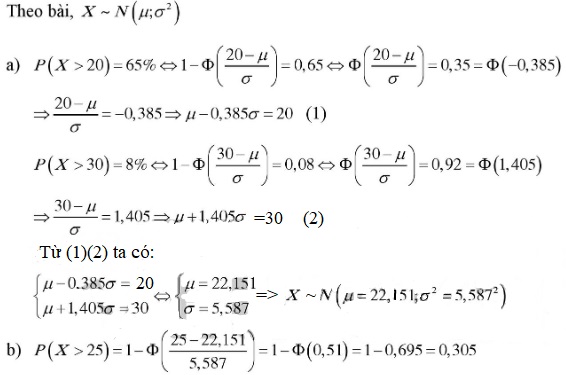
Bài 7: Một ký túc xá của một trường đại học có 650 sinh viên. Xác suất để một sinh viên nội trú đến đọc sách tại thư viện trong một ngày bằng 0,7.
a) Tính xác suất để số sinh viên đến đọc sách tại thư viện trong ngày ít hơn 440 sinh viên.
b) Thư viện cần phải chuẩn bị bao nhiêu ghế ngồi. Để với xác suất 0,99 có thể đảm bảo đủ ghế chỗ cho sinh viên đến đọc sách.
Giải

Bài 8: Lượng truy cập của một Website có dung lượng lớn được giả định tuân theo quy luật phân phối Poisson. Lượng truy cập trung bình là 10 000 truy cập mỗi ngày.
a) Tính xấp xỉ xác suất để có hơn 20 000 truy cập mỗi ngày.
b) Tính xấp xỉ xác suất để ít hơn 9 900 truy cập mỗi ngày.
c) Xác định giá trị mà với xác suất 0,01 thì có lượng truy cập mỗi ngày vượt quá giá trị đó.
Giải

5. Ứng dụng của biến ngẫu nhiên liên tục
- Kinh doanh: Ước tính nhu cầu khách hàng theo thời gian.
- Giáo dục: Mô hình hóa điểm thi của sinh viên.
- Công nghệ: Phân tích thời gian tải trang web.
6. Câu hỏi thường gặp về biến định lượng liên tục
Trong các biến sau, biến nào là định lượng liên tục?
- Màu của xe đạp: Không phải.
- Trọng lượng của quả bí ngô: Đúng.
X là giá tiền sách giáo khoa, X liên tục hay rời rạc?
- X là biến liên tục.
Hi vọng qua bài viết các bạn đã nắm được kiến thức cơ bản về các công thức tính và cách giải bài tập về biến ngẫu nhiên liên tục.
Bài viết cùng chủ đề:
giáo trình xác suất thống kê PDF
kiểm định giả thuyết về giá trị trung bình