Phân phối Poisson, với tên gọi được đặt theo tên của nhà toán học người Pháp Siméon Denis Poisson, là một khái niệm vô cùng quen thuộc trong xác suất thống kê. Sau đây mình xin gửi tới các bạn một số bài tập về bảng phân phối Poisson có đáp án giúp bạn bạn ôn tập dễ dàng.
Xem thêm:
- bảng phân phối xác suất
- phân phối nhị thức là gì: Công thức và bài tập có lời giải
- giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Phân phối Poisson là gì?
Phân phối Poisson là một phân phối xác suất đối với biến cố rời rạc. Phân phối được sử dụng để mô hình hóa số lần xảy ra một sự kiện trong một khoảng thời gian cố định hoặc một không gian cố định. Đặc điểm của phân phối này là tỷ lệ xảy ra các sự kiện là không đổi và độc lập với nhau trong khoảng thời gian hoặc không gian xác định.
Phân phối Poisson có một tham số duy nhất là λ (lambda), biểu thị số lần trung bình xảy ra sự kiện trong một khoảng thời gian cố định, và k, biểu thị số lần xảy ra sự kiện trong khoảng thời gian đó.
2. Công thức phân phối Poisson (Poisson Distribution)
Biến ngẫu nhiên rời rạc X được gọi là có phân phối Poisson với tham số λ, ký hiệu là X∼P (λ), nếu X nhận các giá trị có thể có là các số nguyên không âm: 0, 1, 2, … , n và các suất tương ứng được tính theo công thức xấp xỉ Poisson.
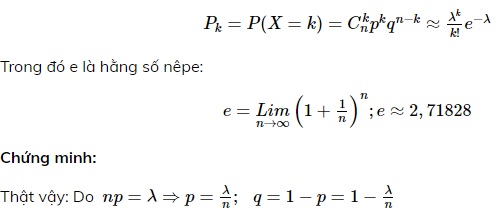
3. Các đặc trưng của phân phối Poisson
Nếu X có phân phối Poisson (X ∼ P (λ )) thì :
![]()
Xem thêm:
- phân phối xác suất thành phần – Các đặc trưng và bài tập
- phân phối xác suất có điều kiện và kỳ vọng có điều kiện
4. Đặc điểm của phân phối Poisson
Xét một biến cố A (“Thành công”) xuất hiện ở những thời điểm ngẫu nhiên.
Giả thiết rằng X số lần biến cố “Thành công” xảy ra trong một đơn vị thời gian hay không gian xác định gọi là một phân đoạn. Khi đó X có phân phối Poisson. Chẳng hạn, số lỗi trên một trang đánh máy; số khách hàng đến giao dịch tại ngân hàng trong khoảng thời gian cụ thể (trong một giờ); số cuộc gọi khẩn cấp nhận được trong 15 phút… đều có phân phối Poisson.
– Xác suất của biến cố “Thành công” cho mỗi một phân đoạn là tương tự cho tất cả các phân đoạn có cùng kích thước.
– Số biến cố “thành công” xảy ra trong một phân đoạn này độc lập với số biến cố “thành công” xảy ra trong phân đoạn khác.
– Nếu chia phân đoạn thành những phân khúc ngày càng nhỏ thì xác xuất biến cố “thành công” xảy ra trong mỗi phân khúc rất nhỏ sẽ rất bé ( P(A) <0,005).
– Giả sử số biến cố “thành công” trung bình trên một đơn vị phân đoạn được chọn là một số ả thi số biến cố “thành công” trung bình trên một phân đoạn cỡ t là 2t (t và t phải cùng đơn vị đo) .
5. Ví dụ bài tập phân phối Poisson
Bài 1: Một mạng lưới máy tính khi bị nghẽn thì một gói dữ liệu có xác suất bị mất là 1% và các gói dữ liệu bị mất là độc lập với nhau. Các gói dữ liệu bị mất này cần phải gửi lại. Một thư điện tử có 100 gói dữ liệu.
a) Cho biết phân phối xác suất của các gói giữ liệu cần phải gửi lại (các gói dữ liệu bị mất trong 100 gói dữ liệu (trong 1 tin nhắn)? Trung bình và độ lệch chuẩn của các gói dữ liệu cần phải gửi lại là bao nhiêu?
b) Tính xác suất để có hai hay nhiều hơn gói dữ liệu cần gửi lại.
c) Nếu có 3 tin nhắn ( mỗi tin nhắn có 100 gói dữ liệu) thì xác suất có ít nhất một tin nhắn có hai hoặc nhiều hơn hai gói dữ liệu phải gửi lại là bao nhiêu?
Giải
a. X có poisson phân phối với n = 100; p = 0,01; q = 0,99
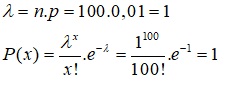
Các gói dữ liệu bị mất, cần gửi lại là: E (X) = 1
b.
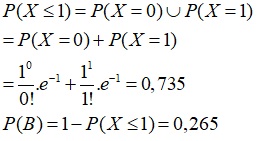
c. Bài toán ý c là cho phép thử Bernoulli với n = 3; p = 0,625
Bài tập xác suất Poisson có lời giải
Bài 2: Xác suất để đoàn tàu khởi hành đúng giờ là 98,2%. Tính xác suất để 1000 chuyến tàu có 995 chuyến tàu khởi hành đúng thời gian.
Giải

Bài 3: Lưu lượng giao thông theo cách truyền thống được coi là có phân phối Poisson. Một trạm kiểm soát điều khiển lưu lượng giao thông ở một nút giao thông với trung bình 6 xe một phút. Để thiết lập thời gian cho đèn tín hiệu thì các xác suất sau đây được sử dụng:
a) Tính xác suất để không có xe nào đi qua nút giao thông trong 30 giây.
b) Tính xác suất có 3 xe hoặc nhiều hơn 3 xe đi qua nút giao thông trong một phút
Giải

Xem thêm:
- Phân phối Fisher – snedecor | Cách tra bảng đầy đủ PDF
- Phân phối t-Student | Cách tra bảng giá trị đầy đủ PDF
- Phân phối đều là gì? Công thức và bài tập có lời giải
Bài tập quy luật Poisson
Bài 4: Số cuộc gọi điện thoại đến trung tâm tổng đài thường được mô tả là một biến ngẫu nhiên Poisson. Biết rẳng trung bình có 10 cuộc điện thoại gọi tới trong 1 giờ.
a) Xác suất có đúng 5 cuộc điện thoại gọi tới trong 1 giờ là bao nhiêu?
b) Xác suất có 3 hoặc ít hơn 3 cuộc điện thoại gọi tới trong 1 giờ là bao nhiêu?
c) Xác suất có đúng 15 cuộc điện thoại gọi tới trong 2 giờ là bao nhiêu?
d) Xác suất có đúng 5 cuộc điện thoại gọi tới trong 30 phút là bao nhiêu?
Giải
a. Gọi X là cuộc gọi đến tổng đài trong 1h. Theo giả thiết X có poisson phân phối với:
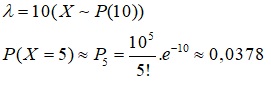
b.
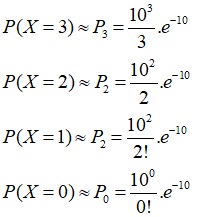
c. Gọi Y là cuộc gọi đến tổng đài trong 2h. Theo giả thiết Y có poisson phân phối với:
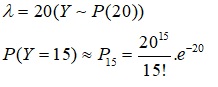
d. Gọi Z là cuộc gọi đến tổng đài trong 30p. Theo giả thiết Z có poisson phân phối với:
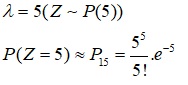
Trên đây là bài viết và cách giải bài tập phân phối Poisson. Hy vọng tài liệu trên sẽ giúp các bạn nắm vững kiến thức về chương này. Cảm ơn các bạn đã tham khảo trên TTnguyen.
Bài viết liên quan:
- Phân phối siêu bội – Công thức và bài tập có lời giải
- Bảng phân phối Chi bình phương, Gamma | Cách tra và bài tập