Công thức Bayes là công thức ngược, cho phép tính xác suất có điều kiện P(B|A) khi biết xác suất có điều kiện P(A|B) và một số thông tin khác. Trong bài viết này, chúng ta sẽ tìm hiểu khái niệm định luật, cách chứng mình và làm một số bài tập cụ thể.
Xem thêm:
- bài tập biểu đồ venn trong xác suất thống kê
- không gian mẫu
- giải bài tập xác suất thống kê chương 1
Định lý bayes là gì?
Định lý Bayes là một định lý trong xác suất và thống kê, được đặt theo tên nhà toán học người Anh Thomas Bayes(1702-1761). Định lý này cho phép tính xác suất của một sự kiện dựa trên thông tin đã biết trước.
Định lý Bayes được áp dụng rộng rãi trong nhiều lĩnh vực, như trí tuệ nhân tạo, thống kê, y học, công nghệ thông tin, và các ngành khoa học khác. Nó cho phép xác định được xác suất của một giả thuyết hay sự kiện dựa trên các thông tin hữu ích đã biết trước đó.
Công thức xác suất Bayes
Dạng đơn giản nhất của công thức này là: Nếu A,B là hai sự kiện bất kì với xác suất khác 0 thì từ quy tắc nhân xác suất:
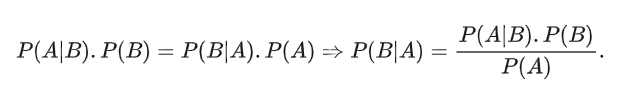
Định lý Bayes:
Cho \(B_{1}, B_{2},…,B_{n}\) là họ đầy đủ các biến cố và xét biến cố A với P(A) > 0. Với mỗi i=1,2,…,n, ta có:
| \(P(H_i|A)=\frac{P(H_i).P(A|H_i)}{\sum_{i=0}^{n}P(H_i).P(A|H_i)}\) |
Các xác suất P(Hi) và P(A/Hi) thường được biết trước khi thực hiện phép thử và được gọi là các xác suất tiền nghiệm, còn các xác suất P(Hi/A), cho biết khả năng tham gia của Hi, vào việc xảy ra biến cố A, được gọi là xác suất hậu nghiệm.
Xem thêm: quy tắc cộng xác suất
Chứng minh công thức Bayes
Áp dụng công thức nhân xác suất:
\(P(A).P(H_i|A)=P(AH_i)=P(H_iA)=P(H_i).P(A|H_i)\)và công thức xác suất toàn phần
\(P(A)=\sum_{i=1}^{n}P(B_i).P(A|B_i)\)ta suy ra:
\(P(H_i|A)=\frac{P(H_i).P(A|H_i)}{P(A)}=\frac{P(H_i).P(A|H_i)}{\sum_{i=0}^{n}P(H_i).P(A|H_i)}\)Bài tập công thức Bayes
Bài 1: Hộp I: 5 bi trắng và 5 bi đen. Hộp II: 6 bi trắng và 4 bi đen. Bỏ hai viên bi từ hộp I sang hộp II. Sau đó lấy ra 1 viên bi.
a. Tính xác suất để lấy được bi trắng.
b. Giả sử lấy được bị trắng, tính xác suất để lấy được bi trắng của hộp I.
Giải

a. Cách 1: P(A)= P(H0).P(A|H0)+ P(H1).P(A|H1)+ P(H2).P(A|H2)=7/12
Cách 2: Gọi K1 là biến cố lấy bi ra từ hộp II của hộp I
Gọi K2 là biến cố lấy bi ra từ hộp II của hộp II
\(P(K1)=\frac{C_{2}^{1}}{C_{12}^{1}}\)
\(P(K2)=\frac{C_{10}^{1}}{C_{12}^{1}}\)
\(P(A|K1)=\frac{C_{5}^{1}}{C_{10}^{1}}\)
\(P(A|K2)=\frac{C_{6}^{1}}{C_{10}^{1}}\)
P(A)=P(K1)P(A|K1)+P(K2)P(A|K2)=7/12
b. \(P(K1|A)=\frac{P(K1)P(A|K1)}{P(A)}=\frac{1}{7}\)
Giải bài tập công thức Bayes
Bài 2: Tan giờ học buổi chiều một sinh viên có 60% về nhà ngay, nhưng do giờ cao điểm nên có 30% ngày bị tắc đường nên bị về nhà muộn (từ 30 phút trở lên) còn 20% số ngày sinh viên đó vào quán Internet cạnh trường để chơi Games, những ngày này xác suất về nhà muộn là 80%. Còn lại những ngày khác sinh viên đó đi chơi với bạn bè có xác suất về muộn là 90%.
a. Tính xác suất để trong một ngày nào đó sinh viên không về muộn.
b. Hôm nay sinh viên đó về muộn. Tính xác suất để để sinh viên đó đi chơi với bạn bè.
Giải
a.Gọi B là biến cố sinh viên đó đi học về muộn
\(\overline{B}\) là biến cố sinh viên đó đi học không về muộn
E1 là biến cố tan học về nhà ngay => P(E1)=0,6, P(B|E1)=0,3
E2 là biến cố tan học đi chơi game => P(E2)=0,2, P(B|E2)=0,8
E3 là biến cố tan học về đi chơi với bạn => P(E3)=0,2 , P(B|E3)=0,9
B có thể xảy ra một trong 3 biến cố
P(B)=P(E1).P(B|E1)+P(E2).P(B|E2)+P(E3).P(B|E3)
=> P(B)=0,52
=> \(P(\overline{B})=0,48\)
b. Xác suất để sinh viên đó đi chơi với bạn là:
\(P(E_3|B)=\frac{P(E_3).P(B|E_3)}{P(B)}=0,375\)
Bài tập bayes
Bài 3: Một loại linh kiện do 3 nhà máy số I, số II, số III cùng sản xuất. Tỷ lệ phế phẩm của các nhà máy lần lượt là : I ; 0,04; II: 0,03 và III: 0,05 .Trong 1 lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I, 120 của nhà máy số II và 100 của nhà máy số III..
a) Một khách hàng lấy ngẫu nhiên 1 linh kiện từ lô hàng đó. Tính XS để được linh kiện tốt.
b) Khách hàng lấy phải một linh kiện loại phế phẩm từ lô hàng đó. Khả năng linh kiện đó do nhà máy nào sản xuất là cao nhất?
Giải
Gọi E1 là biến cố phế phẩm máy số I=> \(P(E1)=0,04, P(\overline{E1})=0,96\)
E2 là biến cố phế phẩm máy số II=> \(P(E2)=0,03, P(\overline{E2})=0,97\)
E3 là biến cố phế phẩm máy số III=> \(P(E3)=0,05, P(\overline{E3})=0,95\)
Gọi B là biến cố khách hàng lấy được 1 linh kiện tốt
a. Xác suất để khách hàng lấy được linh kiện tốt là
\(P(B)= \frac{C_{80}^{1}}{C_{300}^{1}}.0,96+\frac{C_{120}^{1}}{C_{300}^{1}}.0,97+\frac{C_{120}^{1}}{C_{300}^{1}}.0,95\)
\(=0,96\)b. Gọi \(\overline{B}\) là biến cố khách hàng lấy 1 linh kiện loại không tốt
\(P(\overline{B})=1-P(B)=0,04\)
\(P(E1|\overline{B})=\frac{P(E1).P(\overline{B}|E1)}{P(\overline{B})}=\frac{C_{80}^{1}.0,04}{0,04}=0,26\)
\(P(E2|\overline{B})=\frac{P(E2).P(\overline{B}|E2)}{P(\overline{B})}=\frac{C_{120}^{1}.0,03}{0,04}=0,3\)
\(P(E3|\overline{B})=\frac{P(E3).P(\overline{B}|E3)}{P(\overline{B})}=\frac{C_{100}^{1}.0,05}{0,04}=0,41\)
Vậy linh kiện đó do máy III là cao nhất
Công thức bayes dùng khi nào?
Công thức Bayes được sử dụng trong các bài toán xác suất và thống kê để tính toán xác suất điều kiện dựa trên thông tin có sẵn. Một số trường hợp khi cần sử dụng công thức Bayes bao gồm:
1. Khi có thông tin xác suất ban đầu và muốn tính toán xác suất sau khi có thêm thông tin mới.
2. Khi có thông tin xác suất rời rạc (discrete) và muốn tính toán xác suất xảy ra của một sự kiện khác.
3. Khi muốn tính toán xác suất hậu nghiệm (posterior probability) của một giả thuyết dựa trên dữ liệu thực tế.
4. Khi muốn tính toán xác suất của một giả thuyết dựa trên xác suất liên tục (uniform prior probability).
5. Khi muốn phân loại dữ liệu dựa trên các đặc trưng và thông tin xác suất đã biết.
Dùng công thức Bayes giúp tối ưu hóa việc tính toán xác suất và đưa ra các quyết định dựa trên thông tin có sẵn. Cảm ơn bạn đã theo dõi trên ttnguyen.net.
Tải tài liệu định luật bayes PDF:
Bài viết liên quan: