Công thức xác suất đầy đủ là một trong những công thức quan trọng trong học tập cũng như được ứng dụng nhiều trong đời sống. Sau đây TTnguyen xin gửi tới bạn một số bài tập công thức xác suất đầy đủ trong môn Xác suất thống kê.
Xem thêm:
- Biểu đồ Venn trong xác suất thông kê – Bài tập có lời giải chi tiết
- không gian mẫu
1. Xác suất đầy đủ là gì?
1.1 Hệ đầy đủ các biến cố
Nhóm các biến cố A1, A2, … An của một phép thử được gọi là một nhóm đầy đủ nếu:

1.2 Ví dụ một nhóm đầy đủ
Ví dụ 1: Một tiểu đoàn có 3 đại đội cùng trồng một loại bí xanh. Chọn ngẫu nhiên một quả bí xanh và gọi {A1,A2,A3} lần lượt là sự kiện quả bí xanh được chọn do đại đội 1, đại đội 2 và đại đội 3 trồng. Khi đó hệ {A1,A2,A3} là đầy đủ.
Ví dụ 2: Gieo một con xúc xắc.
Gọi Bi là biến cố “nhận được mặt có i chấm”.
Các biến cố B1 ,B2 ,…,B6 tạo nên một họ đầy đủ các biến cố.
2. Công thức tính xác suất đầy đủ
Với H1, H2, H3 nhóm đầy đủ biến cố, công thức xác suất đầy đủ là:
| P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) |
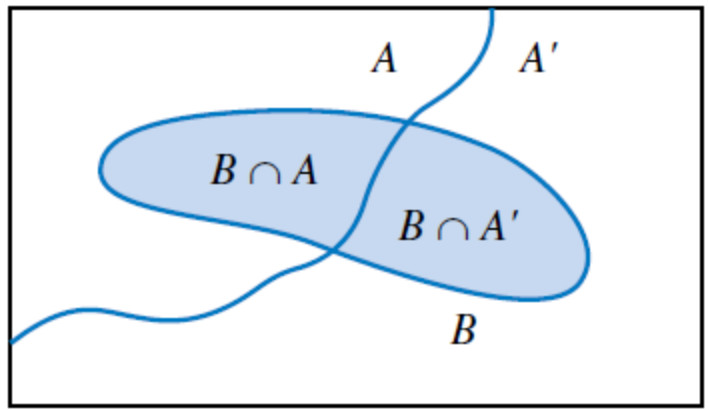
3. Chứng minh công thức xác suất đầy đủ
Do \(BA\) và \(\bar{B}A\) là hai biến cố xung khắc và \(A= BA + \bar{B}A\) nên:
\(P(A) = P(BA + \bar{B}A)\\\) \(= P(BA) + P(\bar{B}A)\\\) \(= P(B)P(A|B) + P(\bar{B})P(A|\bar{B})\\\)Tổng quát, do các biến cố \(B_{1}A, B_{2}A,…,B_{n}A\) xung khắc từng đôi một và \(A=B_{1}A, B_{2}A,…,B_{n}A\) nên do công thức cộng xác suất:
\(P(A)=P(B_{1}A, B_{2}A,…,B_{n}A)\\\) \(=P(B_{1}A)+P(B_{2}A)+..+P(B_{n}A)\\\) \(=P(B_{1})P(A|B_{1})+…+P(B_{n})P(A|B_{n})\\\) \(=\sum_{i=1}^{n}P(B_{i})P(A|B_{i})\\\)và do công thức nhân xác suất,
\(P(B_{i}A)=P(B_{i})P(A|B_{i})\\\)với mọi i ta suy ra
\(P(A)=\sum_{i=1}^{n}P(B_{i})P(A|B_{i})\)4. Ví dụ về công thức xác suất đầy đủ
Bài 1: Một hộp có 4 viên bi, mỗi viên bi có thể gồm hai màu đen và trắng. Lấy ngẫu nhiên ra 2 viên bi. Tính xác suất để lấy được 2 bi trắng
Hướng dẫn giải
H4 4 bi trắng P(A|H4)= \(\frac{\mathrm{C}_{4}^{2}}{\mathrm{C}_{4}^{2}}\) =1
H3 3 trắng, 1 đen P(A|H3)=\(\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{4}^{2}}\)=1/2
H2 2 trắng, 2 đen P(A|H2)=1/6
H1 1 trắng, 3 đen P(A|H1)=0
H0 0 trắng, 4 đen P(A|H0)=0
Gọi A là biến cố lấy được 2 bi trắng
=> P(A)= P(H4)P(A|H4)+P(H3)P(A|H3) +P(H2)P(A|H2)+P(H1)P(A|H1)+P(H0)P(A|H0)
=0,2.1+0,2.1/2+0,2.1/6+0+0=1/3
5. Bài tập công thức xác suất đầy đủ
Bài 2: Có hai hộp đựng phiếu thi, mỗi phiếu ghi một câu hỏi. Hộp thứ nhất có 15 phiếu và hộp thứ hai có 9 phiếu. Sinh viên A đi thi chỉ thuộc 10 câu ở hộp thứ nhất và 8 câu ở hộp thứ hai.
a. Thầy giáo rút ngẫu nhiên từ mỗi hộp ra một phiếu thi, sau đó cho sinh viên A rút ngẫu nhiên ra 1 phiếu từ 2 phiếu mà thầy giáo đã rút. Tính xác suất để sinh viên A trả lời được câu hỏi trong phiếu .
b) Thầy giáo rút ngẫu nhiên ra 1 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 1 phiếu từ hộp thứ hai. Tính xác suất để sinh viên trả lời được câu hỏi trong phiếu.
c) Thầy giáo rút ngẫu nhiên ra 2 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 2 phiếu từ hộp thứ hai
Hướng dẫn giải
a.Gọi E1 là biến cố sinh viên rút ra từ hộp 1
E2 là biến cố sinh viên rút ra từ hộp 2
E1, E2 tạo thành một nhóm biến cố đầy đủ
Gọi B là biến cố rút ra 1 câu thuộc B=(E1∩B)∪(E2∩B)
=> P(B) = P(E1)P(B|E1) + P(E2)P(B|E2)
\(P(E1)=\frac{C_{1}^{1}}{C_{2}^{1}}=\frac{1}{2}\)
\(P(E2)=\frac{C_{1}^{1}}{C_{2}^{1}}=\frac{1}{2}\)
\(P(B|E1)=\frac{C_{10}^{1}}{C_{15}^{1}}=\frac{2}{3}\)
\(P(B|E2)=\frac{C_{8}^{1}}{C_{9}^{1}}=\frac{8}{9}\)
=> P(B)=\(\frac{7}{9}\)
b.Gọi E1 là biến cố thầy giáo rút 1 câu thuộc từ hộp 1 bỏ vào hộp 2. Khi đó hộp 2 có 9 câu thuộc và 1 câu không thuộc.
Gọi E2 là biến cố thầy giáo rút 1 câu không thuộc từ hộp 1 bỏ vào hộp 2. Khi đó hộp 2 có 8 câu thuộc và 2 câu không thuộc.
E1,E2 tạo thành một nhóm biến cố đầy đủ. B xảy ra với 1 trong 2 biến cố.
B=(E1∩B)∪(E2∩B)
=> P(B)=P(E1)P(B|E1)+P(E2)P(B|E2)
\(P(E1)=\frac{C_{10}^{1}}{C_{15}^{1}}=\frac{2}{3}\)
\(P(E2)=\frac{C_{5}^{1}}{C_{15}^{1}}=\frac{1}{3}\)
\(P(B|E1)=\frac{C_{9}^{1}}{C_{10}^{1}}=\frac{9}{10}\)
\(P(B|E2)=\frac{C_{8}^{1}}{C_{10}^{1}}=\frac{4}{5}\)
P(B)=0,942
c.Gọi E1 là biến cố thầy giáo rút 2 câu thuộc từ hộp 1 bỏ sang hộp 2
Gọi E2 là biến cố thầy giáo rút 1 câu thuộc và 1 câu không thuộc từ hộp 1 bỏ sang hộp 2
Gọi E3 là biến cố thầy giáo rút 2 câu không thuộc từ hộp 1 bỏ sang hộp 2
Gọi C là biến cố sinh viên rút ra 2 câu thuộc từ hộp 2
P(C)=P(E1)P(C|E1)+P(E2)P(C|E2)+P(E3)P(C|E3)
\(P(E1)=\frac{C_{10}^{2}}{C_{15}^{2}}=\frac{3}{7}\)
\(P(E2)=\frac{C_{10}^{1}.C_{5}^{1}}{C_{15}^{2}}=\frac{10}{21}\)
\(P(E3)=\frac{C_{5}^{2}}{C_{15}^{2}}=\frac{2}{21}\)
\(P(C|E1)=\frac{C_{10}^{2}}{C_{11}^{2}}=\frac{9}{11}\)
\(P(C|E2)=\frac{C_{9}^{2}}{C_{11}^{2}}=\frac{12}{35}\)
\(P(C|E3)=\frac{C_{8}^{2}}{C_{11}^{2}}=\frac{3}{55}\)
6. Bài tập về công thức xác suất đầy đủ có lời giải
Bài 3: Có 2 xạ thủ loại I và 8 xạ thủ loại II, xác suất bắn trúng đích của các loại xạ thủ loại I là 0,9 và loại II là 0,7.
a) Chọn ngẫu nhiên ra một xạ thủ và xạ thủ đó bắn một viên đạn. Tìm xác suất để viên đạn đó trúng đích.
b) Chọn ngẫu nhiên ra hai xạ thủ và mỗi người bắn một viên đạn. Tìm xác suất để cả hai viên đạn đó trúng đích.
Giải

Tải file tài liệu công thức xác suất toàn phần PDF:
Ok xong, vừa rồi TTnguyen đã gợi ý cách giải bài tập công thức xác suất đầy đủ qua một số bài toán cơ bản. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net
Câu hỏi liên quan
1. Khi nào dùng công thức xác suất đầy đủ, khi nào dùng công thức bayes?
Công thức xác suất đầy đủ được sử dụng trong trường hợp xác suất không điều kiện, công thức bayes sử dụng trong trường hợp xác xuất có điều kiện.
Bài viết liên quan: