Phân phối T thường được áp dụng cho các bài toán liên quan đến ước lượng tham số dựa trên mẫu, khi ta không biết phương sai. Với độ tin cậy cao, bảng phân phối student cho phép ta rút ra những kết luận chính xác hơn trong việc đưa ra quyết định với số liệu bị ảnh hưởng bởi sự biến động ngẫu nhiên.
Xem thêm:
- phân phối nhị thức là gì: Công thức và bài tập có lời giải
- phân phối poisson là gì? Công thức, quy luật và bài tập
- phân phối xác suất thành phần – Các đặc trưng và bài tập
1. Bảng phân phối Student là gì?
Phân phối Student (hay phân phối t-Student) là một loại phân phối xác suất được sử dụng trong thống kê. Phân phối này được đặt tên theo tên một nhà thống kê người Anh, William Gosset, người sử dụng nhiều phân phối này để nghiên cứu về biến độc lập nhỏ.
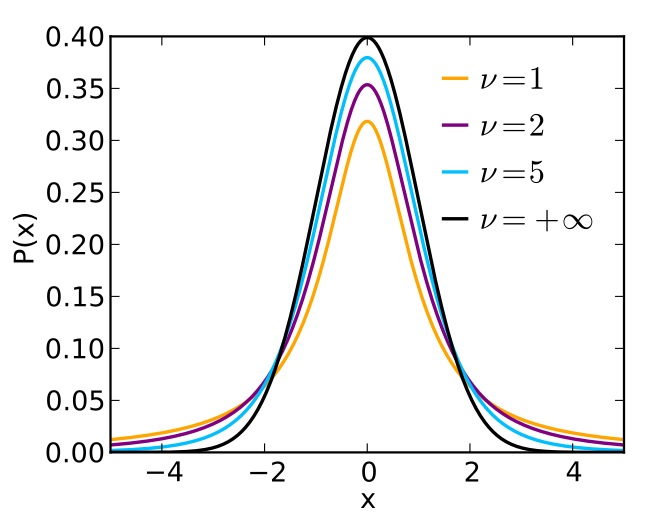
Phân phối này có dạng hình chuông, đối xứng quanh giá trị trung bình là 0, và có hình dạng phụ thuộc vào số bậc tự do (df). Khi số bậc tự do tăng lên, phân phối Student tiến gần đến phân phối chuẩn.
Công thức xác định phân phối Student:
Biến ngẫu nhiên liên tục T được gọi là có phân phối Student. Ký hiệu \(T∼ St(n)\) hoặc \(X ∼ T_n \) nếu hàm mật độ của T có dạng sau:
\(f(t)=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n \pi}.\Gamma\left( \frac{n}{2} \right).\left( 1+\frac{t^2}{n} \right)^{\frac{n+1}{2}}}\)2. Đồ thị phân phối Student
Đặc điểm của đồ thị phân phối T:
- Có dạng hình chuông và đối xứng.
- Giá trị trung tâm là 0.
- Diện tích vùng dưới đường cong = 1.
- Phân phối t là tiệm cận.
- Có hình dạng phụ thuộc và bậc tự do (df).
- df→ ∞, phân phối t giống phân phối chuẩn.
Tính chất của phân phối T:
- Trung bình: \(\mu_T = 0\)
- Phương sai: \(\sigma^2_T = \frac{n}{n-2}\)
Cho X là biến ngẫu nhiên liên tục có phân phối Gauss, \(X ∼ N(0, 1) ;\) Y là biến ngẫu nhiên liên tục có phân phối chi bình phương với n bậc tự do, \(Y \sim \chi ^ 2(n)\) và X, Y là hai biến độc lập.
Khi đó \(T=\frac{X}{\sqrt{Y /_ n}} \) có phân phối Student với n bậc tự do, \(T∼ St(n)\).
Xem thêm:
- phân phối xác suất có điều kiện và kỳ vọng có điều kiện
- phân phối xác suất đồng thời – Cách lập bảng có đáp án
3. Bảng giá trị phân phối Student đầy đủ PDF
File tải bảng phân phối Student PDF bản đầy đủ:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
4. Cách tra bảng phân phối Student
Để tra bảng phân phối Student, bạn cần biết hai thông số quan trọng: số độ tự do (degrees of freedom) và mức ý nghĩa (significance level).
1. Số độ tự do (degrees of freedom): Số độ tự do thường được ký hiệu là “df” và được tính bằng tổng số quan sát trong mẫu trừ đi 1. Số độ tự do là quan trọng vì nó ảnh hưởng đến hình dạng của phân phối T. Để tra bảng, bạn cần xác định giá trị độ tự do cho mẫu của mình.
2. Mức ý nghĩa (significance level): Mức ý nghĩa thường được ký hiệu là “α” và đại diện cho xác suất chấp nhận sai lầm loại 1 (tức là bác bỏ sai một giả thuyết đúng). Mức ý nghĩa thông thường là 0.05 hoặc 0.01. Mức ý nghĩa càng nhỏ, độ chặt chẽ của quyết định càng cao.
Sau khi xác định số độ tự do và mức ý nghĩa, bạn có thể sử dụng bảng phân phối T để tra giá trị tương ứng.
Xem thêm:
- bảng phân phối fisher – snedecor | Cách tra bảng đầy đủ PDF
- phân phối đều là gì? Công thức và bài tập có lời giải
5. Bài tập phân phối Student có lời giải
Bài 1: Tuổi thọ trung bình của 10 bóng đèn điện được chọn ngẫu nhiên là 4000 giờ, độ lệch chuẩn của mẫu là 200 giờ. Giả thiết phân bố tuổi thọ bóng đèn là phân phối chuẩn. Với độ tin cậy 95% hãy ước lượng khoảng tin cậy của tuổi thọ trung bình của bóng đèn.
Giải
Với độ tin cậy 95%, từ bảng tra phân phối Student với bặc tự do bằng 9 ta có:
\(t_{a/2;(n-1)}=2.626\), do đó khoảng tin cậy sẽ là:
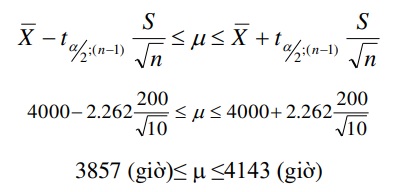
Kết luận: Với độ tin cậy 95%, thì tuái thọ của loại bóng đèn nêu trên nằm trong khoảng [3857;4143]
6. Ứng dụng của bảng phân phối Student
Bảng phân phối Student được sử dụng trong nhiều lĩnh vực như thống kê, khoa học dữ liệu, kế toán, kinh tế học và nhiều lĩnh vực khác. Dưới đây là một số ứng dụng phổ biến của bảng:
1. Kiểm định giả thuyết thống kê: Bảng phân phối T được sử dụng để kiểm tra giả thuyết về sự khác biệt giữa hai mẫu độc lập. Bạn có thể so sánh trung bình của hai mẫu để xem liệu chúng có khác biệt đáng kể hay không.
2. Xây dựng khoảng tin cậy: Bảng phân phối cũng được sử dụng để ước lượng khoảng tin cậy cho trung bình của một mẫu. Khoảng tin cậy giúp định vị giá trị trung bình ước lượng và độ chính xác của ước lượng đó.
3. Phân tích phương sai: Trong một phân tích phương sai (ANOVA), bảng phân phối T được sử dụng để tính toán F-statistic, một chỉ số quan trọng để kiểm tra sự khác biệt giữa các nhóm trong mẫu.
4. Xác suất: Cuối cùng, bảng được sử dụng để tính toán xác suất của một biến ngẫu nhiên có phân phối T trong các phép toán thống kê phức tạp hơn.
Tổng kết lại, bảng phân phối t-Student là một công cụ quan trọng trong xác suất thống kê. Bảng cho phép chúng ta xác định khoảng tin cậy và kiểm tra giả thuyết về các ước lượng thống kê. Cảm ơn bạn đã tham khảo trên ttnguyen.net.
Bài viết liên quan:
phân phối mũ – Công thức tính và bài tập có lời giải
phân phối siêu bội – Công thức và bài tập có lời giải
giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
tổng hợp công thức tính xác suất thống kê đại học
bài tập biến ngẫu nhiên 2 chiều rời rạc có lời giải