Ma trận bậc thang trong toán cao cấp đại số tuyến tính là một dạng đặc biệt của ma trận, trong đó các hàng không chỉ chứa các giá trị không và các phần tử đầu của mỗi hàng không bằng không, mà nó còn có thêm tính chất các phần tử khác không đầu hàng trên hàng dưới nó. Trong bài viết này, chúng ta sẽ khám phá ma trận bậc thang là gì và các dạng bài tập liên qua nhé.
Xem thêm:
I. Ma trận bậc thang là gì
Ma trận bậc thang là một dạng ma trận đặc biệt trong đó các hàng có đặc điểm sau:
- Dòng bằng 0 nằm dưới các dòng khác 0 (nếu có).
- Hệ số khác 0 đầu tiên (bên trái) của dòng dưới nằm về bên phải cột chứa hệ số khác 0 đầu tiên (bên trái của dòng đầu tiên)
Dưới đây là một ví dụ về ma trận bậc thang:
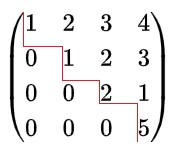
- Ví dụ về ma trận bậc thang:
1 & 2 & 3 & 4 \\
0 & 1 & 2 & 3 \\
0 & 0 & 1 & 2 \\
0 & 0 & 0 & 1
\end{matrix}\right)
\left(\begin{matrix}
2 & 3 & 4 & 5 \\
0 & 2 & 1 & 3 \\
0 & 0 & 3 & 2 \\
0 & 0 & 0 & 4
\end{matrix}\right)
\left(\begin{matrix}
3 & 4 & 2 & 1 \\
0 & 2 & 1 & 3 \\
0 & 0 & 0 & 5 \\
0 & 0 & 0 & 0
\end{matrix}\right)\)
- Ví dụ về ma trận không phải hình thang:
2 & 4 & 6 \\
9 & 3 & 5 \\
0 & 0 & 1 \\
0 & 0 & 0
\end{matrix}\right)
\left(\begin{matrix}
1 & 2 & 3 \\
0 & 4 & 5 \\
6 & 0 & 7
\end{matrix}\right)
\left(\begin{matrix}
3 & 4 & 2 & 1 \\
0 & 2 & 1 & 3 \\
0 & 0 & 0 & 5 \\
0 & 0 & 1 & 2
\end{matrix}\right)\)
II. Ma trận bậc thang rút gọn là gì?
Ma trận bậc thang rút gọn là ma trận ta có thể loại bỏ các phần tử không cần thiết và chỉ giữ lại thông tin cần thiết để tính toán, từ đó giảm thiểu sai số và tăng tốc quá trình tính toán.
Bài viết liên quan:
- hạng của ma trận
- bài tập và cách tìm ma trận chuyển cơ sở
- ma trận kề
III. Các phép biến đổi sơ cấp của ma trận
- Đổi chỗ hai hàng (hai cột) cho nhau.
- Nhân một hàng (một cột) với một số khác không.
- Nhân một hàng (một cột) với một số rồi đem cộng vào một hàng khác (cột khác).
Chú ý: Các phép biến đổi sơ cấp của ma trận đóng vai trò rất quan trọng khi tính định thức, khi giải hệ phương trình tuyến tính…
IV. Đưa ma trận về dạng bậc thang
Bài 1: Chuyển ma trận về dạng bậc thang
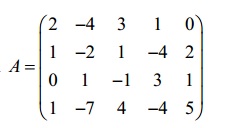

2.Biến đổi ma trận bậc thang
Bài 1:

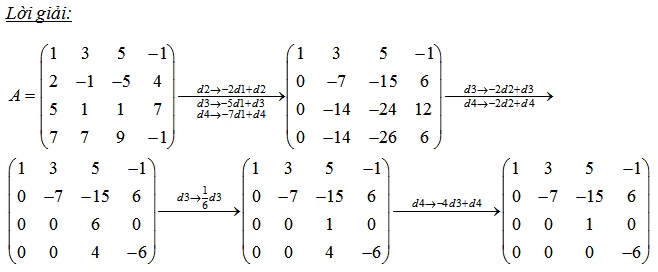
Bài 2:


V. Bài tập ma trận bậc thang có lời giải
Bài 1:
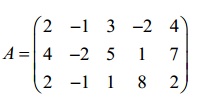
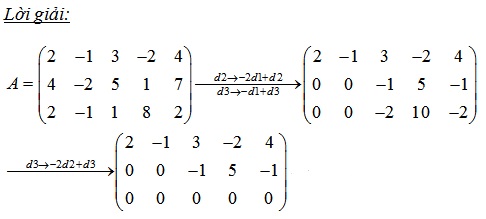
Bài 2:
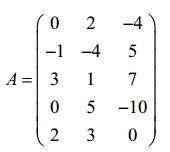

Trên đây là những thông tin và hướng dẫn cơ bản về ma trận bậc thang. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Bài viết tiếp theo: