Bài viết dưới đây sẽ giúp bạn hiểu về bảng phân phối xác suất đồng thời, cách tính hiệp phương sai, hệ số tương quan qua một số bài tập có lời giải.
Xem thêm:
- phân phối nhị thức là gì: Công thức và bài tập có lời giải
- phân phối poisson là gì? Công thức, quy luật và bài tập
- giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Bảng phân phối xác suất đồng thời là gì?
Bảng phân phối xác suất đồng thời là một bảng thể hiện xác suất của một biến ngẫu nhiên đồng thời xảy ra hai sự kiện cùng một lúc. Bảng này có thể được sử dụng để:
- Tính xác suất của các sự kiện kết hợp.
- Phân tích mối quan hệ giữa hai biến ngẫu nhiên.
Cấu trúc bảng:
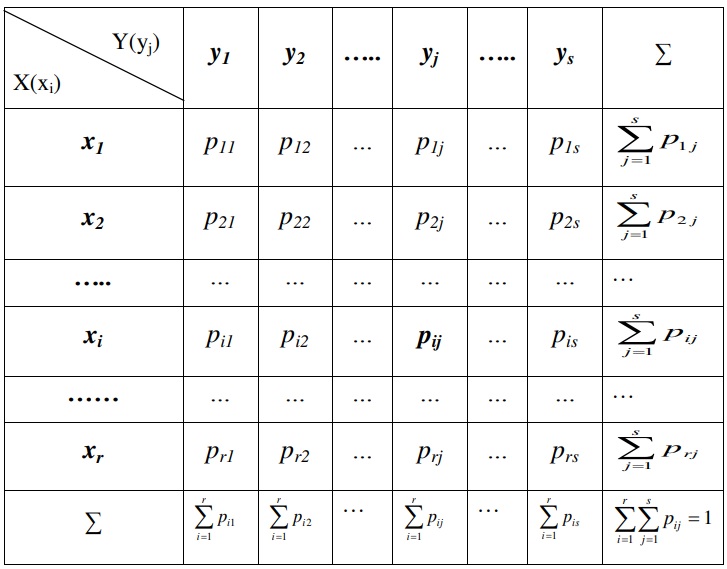
Bảng phân phối xác suất đồng thời thường có dạng một ma trận hai chiều:
- Hàng: Thể hiện giá trị của biến ngẫu nhiên X.
- Cột: Thể hiện giá trị của biến ngẫu nhiên Y.
- Phần tử pij: Xác suất để X=xi đồng thời Y=yj.
Công thức tính:
\(p_{ij}= P[(X=x_i) ∩ (Y=y_j)]\)hoặc \(P_{ij}= P(X=x_i; Y= y_j)\)
Ví dụ: Giả sử hai biến ngẫu nhiên X và Y có bảng phân phối xác suất đồng thời như sau:
| Y\X | 1 | 2 | 3 |
| 2 | 0.2 | 0.2 | 0.1 |
| 3 | 0.1 | 0.3 | 0.1 |
2. Hiệp phương sai
Hiệp phương sai được sử dụng để đo lường mối quan hệ tuyến tính giữa hai biến ngẫu nhiên.
Ký hiệu: Cov(X,Y)), được xác định như sau:
\(cov(X,Y) = E[(X – E(X))(Y – E(Y))] = E(XY) – E(X)E(Y)\)
Cách tính từ bảng phân phối:
\(cov(X,Y) = \sum_{i=1}^{r}\sum_{j=1}^{s}x_iy_jp_{ij} – E(X)E(Y) \)
Một số lưu ý:
– Nếu X và Y là các biến cố độc lập thì Cov(X,Y)=0 (X và Y không tương quan). Tuy nhiên nếu Cov(X,Y)=0 thì X và Y chưa chắc đã độc lập.
– Nếu Cov(X,Y) ≠ 0, thì X và Y không độc lập hay giữa X và Y có mối liên hệ tương quan. Khi đó ta có \(V(\alpha X ± \beta Y) = \alpha^2 V(X) + \beta^2 V(Y) ± 2\alpha\beta cov(X,Y)\)
3. Hệ số tương quan
Hệ số tương quan là thước đo mức độ liên hệ tuyến tính giữa hai biến ngẫu nhiên.
Ký hiệu: \(\rho(X,Y)\), được xác định như sau:
\(\rho(X,Y) = \frac{\text{Cov}(X,Y)}{\sigma(X)\sigma(Y)}\)
Trong đó:
\(\sigma(X)\) và \(\sigma(Y)\)là độ lệch chuẩn tương ứng của X và Y.
Một số tính chất của hệ tương quan:
\(cov(X,Y) > 0\) X và Y tương quan dương (cùng chiều).
\(cov(X,Y) < 0\) X và Y tương quan âm (ngược chiều).
\(|\rho(X, Y)| ≤ 1\\\) \(\rho(X,Y) = \rho(Y, X)\\\)\(|\rho(X, Y)| = 1\) (hay \(|\rho(X, Y)|≈1\)) thì giữa X và Y có mối tương quan tuyến tính, nghĩa là:
\(Y= aX+b \) hoặc \(X= cY+ d\).
Nếu \(\rho(X, Y) > 0\) thì giữa X và Y có mối tương quan thuận. Nếu \(\rho(X, Y) < 0\) thì giữa X và Y có mối tương quan nghịch.
Xem thêm:
- bảng phân phối fisher – snedecor | Cách tra bảng đầy đủ PDF
- bảng phân phối student | Cách tra bảng giá trị đầy đủ PDF
- phân phối xác suất thành phần – Các đặc trưng và bài tập
4. Bài tập phân phối xác suất đồng thời
Bài 1: Tính hiệp phương sai và hệ tương quan sau:
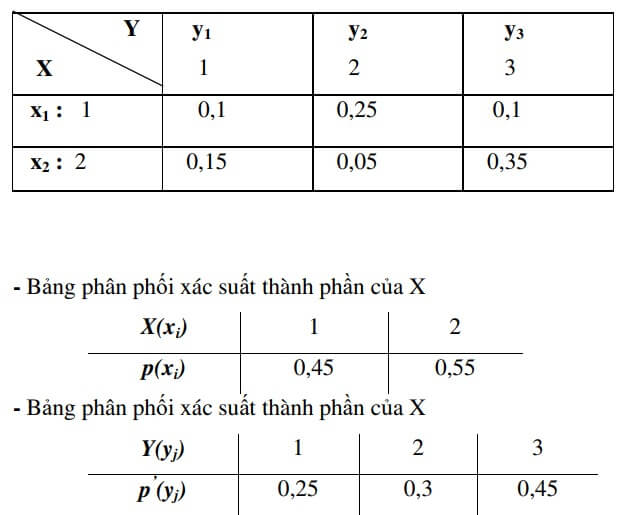
= (1.1.0,1 + 1.2.0,25 + 1.3.0,1 + 2.1.0,15 + 2.2.0,05 + 2.3.0,35 – 1,55.2,2 = 0,09\\
\rho(X,Y) = \frac{Cov(X,Y)}{\sigma(x)\sigma(Y)} = \frac{0,09}{0,4975.0,812}=0,222\)
Bài 2: Lợi nhuận (tỉ đồng) khi đầu tư vào hai dự án A, B lần lượt là các biến ngẫu nhiên X, Y có phân phối xác suất đồng thời:
| Y\X | 1 | 2 | 3 |
| 2 | 0,2 | 0,2 | 0,1 |
| 3 | 0,1 | 0,3 | 0,1 |
1. Tính xác suất từ bảng
2. Tìm bảng phân phối xác suất biên theo các biến và tính các tham số đặc trưng tương ứng
3. Tính hiệp phương sai, hệ số tương quan.
4. Tính kì vọng, phương sai của các hàm 2 biến ngẫu nhiên: Z = aX + bY +c. Đầu tư vào cả A và B theo tỉ lệ vốn lần lượt là 20% – 80%. Tính lợi nhuận trung bình và rủi ro đó của phương án này.
Giải
1. Tính xác suất từ bảng
P(X > 1) = 1 – P(X ≤ 1) = 1 – P(X = 1)= 1- [P(X = 1; Y = 2) + P(X = 1; Y = 3)] = 0,7
P(X > Y) = P(X = 3; Y = 2) = 0,2
P(X + Y < 5) = P(X = 1; Y = 2) +P(X = 1; Y = 3) +P(X = 2; Y = 2) = 0,2 +0,1 +0,2 = 0,5
2. Bảng phân phối xác suất thành phần

E(X) = 1,9 ; E(Y) = 2,5
V(X) = 0,49 ; V(Y) = 0,25
3. Tính hiệp phương sai, hệ số tương quan:
E(XY) = 0,2.2.1 + 0,2.2.2 + 0,1.3.2 + 0,1.1.3 + 0,3.2.3 + 0,1.3.3 = 4,8
Cov(X, Y) = 4,8 – 1,9.2,5 = 0,05 >0
\(\rho(X,Y) = \frac{Cov(X,Y)}{\sigma(x)\sigma(Y)} = \frac{0,05}{\sqrt{0,49}.\sqrt{0,25}}=0,143\)4. Tính kì vọng, phương sai của các hàm 2 biến ngẫu nhiên
Gọi Z : lợi nhuận (tỉ đồng) khi đầu tư vào cả A và B theo tỉ lệ vốn lần lượt là 20% – 80% =>
Z = 0,2X+0,8Y
E(Z) = E(0,2X + 0,8Y) = 0,2E(X) + 0,8E(Y) = 0,2.1,9 + 0,8.2,5 = 2,38 (tỉ đồng)
\(V(Z) = V(0,2X + 0,8Y) = 0, 2^2 V (X) + 0, 8^2 V(Y) +2.0,2.0,8Cον(Χ.Y) = 0,1956\)Bài 3: Cho X, Y là các biến ngẫu nhiên độc lập với phân phối xác suất như sau:
| X | 1 | 2 | 3 |
| P | 0,3 | 0,3 | 0,4 |
| Y | -1 | 0 | 1 |
| P | 0,4 | 0,3 | 0,3 |
a) Tìm phân phối xác suất của Z = X + Y
b) Tìm phân phối xác suất của T = X. Y
c) Tìm phân phối đồng thời của (X, Y)
Giải
a) Bảng phân phối xác suất của Z = X + Y
| Y\X | 1 | 2 | 3 |
| -1 | 0
0,12 |
1
0,12 |
2
0,16 |
| 0 | 1
0,09 |
2
0,09 |
3
0,12 |
| 1 | 2
0,09 |
3
0,09 |
4
0,12 |
| Z | 0 | 1 | 2 | 3 | 4 |
| P | 0,12 | 0,21 | 0,34 | 0,21 | 0,12 |
b) Tìm phân phối xác suất của T = X. Y
| Y\X | 1 | 2 | 3 |
| -1 | -1
0,12 |
-2
0,12 |
-3
0,16 |
| 0 | 0
0,09 |
0
0,09 |
0
0,12 |
| 1 | 1
0,09 |
2
0,09 |
3
0,12 |
| T | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| P | 0,16 | 0,12 | 0,12 | 0,3 | 0,09 | 0,09 | 0,12 |
c) Tìm phân phối đồng thời của (X, Y)
| Y\X | 1 | 2 | 3 |
| -1 | 0,12 | 0,12 | 0,16 |
| 0 | 0,09 | 0,09 | 0,12 |
| 1 | 0,09 | 0,09 | 0,12 |
Bảng phân phối xác suất đồng thời có thể được sử dụng để tính toán xác suất của các sự kiện kết hợp, như xác suất của sự kiện “X=1 hoặc Y=2”, và tìm hiểu mối quan hệ giữa hai biến, như mức độ phụ thuộc giữa X và Y. Cảm ơn các bạn đã tham khảo xác suất thống kê trên ttnguyen.net.
Bài viết liên quan:
phân phối đều là gì? Công thức và bài tập có lời giải
phân phối mũ – Công thức tính và bài tập có lời giải
phân phối siêu bội – Công thức và bài tập có lời giải
bảng phân phối chi bình phương, Gamma | Cách tra và bài tập