Thống kê suy diễn đóng vai trò quan trọng trong việc hiểu và phân tích thông tin từ dữ liệu mẫu nhằm rút ra kết luận về tổng thể. Trong bài viết này, hãy cùng TTnguyen tìm hiểu định nghĩa, các phương pháp suy diễn và bài tập thống kê suy diễn có lời giải.
Xem thêm:
- Ví dụ về tổng thể và mẫu – Bài tập có lời giải
I. Thống kê suy diễn là gì?
Thống kê suy diễn là quá trình sử dụng các quy tắc, phương pháp thống kê để rút ra kết luận về tổng thể dựa trên những thông tin tái diễn từ một mẫu nhỏ được lấy ra từ tổng thể đó. Nó giúp chúng ta ước lượng và kiểm định những giả định, đưa ra quyết định dựa trên số liệu mẫu.
II. Suy đoán về giá trị trung bình mẫu
Khoảng suy diễn tối đa (bên trái) cho \(\overline{X}\) là:
\(\overline{X} < \mu + \frac{\sigma}{\sqrt{n}}z_a\)
Khoảng suy diễn tối thiểu (bên phải) cho \(\overline{X}\) với mức xác suất 1 – α là:
\(\overline{X} > \mu – \frac{\sigma}{\sqrt{n}}z_a\)
Khoảng suy diễn hai phía (đối xứng) cho \(\overline{X}\) là:
\(\mu – \frac{\sigma}{\sqrt{n}z_{\frac{\alpha}{2}}} < \overline{X} < \mu + \frac{\sigma}{\sqrt{n}z_{\frac{\alpha}{2}}}\)
III. Suy đoán về giá trị phương sai mẫu
Khoảng suy diễn tối đa cho \(S^2\) với mức xác suất 1 – α là:
\(S^2 > \frac{\sigma^2}{n-1}X_{1- \alpha}^{2(n-1)}, S^{*2} = \frac{\sigma^2}{n}X_{1- \alpha}^{2(n)}\)Khoảng suy diễn hai phía cho \(S^2\) là:
\(\frac{\sigma^2}{n-1}X_{1- \frac{\alpha}{2}}^{2(n-1)} < S^2 < \frac{\sigma^2}{n-1}X_{\frac{\alpha} {2}}^{2(n-1)} \\ \frac{\sigma^2}{n}X_{1- \frac{\alpha}{2}}^{2(n)} < S^{*2} < \frac{\sigma^2}{n}X_{\frac{\alpha} {2}}^{2(n)} \\ \)IV. Suy đoán về giá trị tần suất mẫu
Khoảng suy diễn tối thiểu cho \(\overline{X}\) với mức xác suất 1 – α là:
\(\hat{p} > p-\frac{\sqrt{p(1-p)}}{\sqrt{n}}z_a\)Khoảng suy diễn tối đa cho \(\overline{X}\) là:
\(\hat{p} < p +\frac{\sqrt{p(1-p)}}{\sqrt{n}}z_a\)Khoảng suy diễn hai phía cho \(\overline{X}\) là:
\(p -\frac{\sqrt{p(1-p)}}{\sqrt{n}}z_a< \hat{p} < p +\frac{\sqrt{p(1-p)}}{\sqrt{n}}z_a\)V. Bài tập suy diễn thống kê có lời giải
Ví dụ 1: Theo thống kê, thời gian xem TV trong tuần của một học sinh tiểu học là biến ngẫu nhiên phân phối chuẩn với trung bình là 15 giờ và độ lệch chuẩn bằng 6 giờ. Khảo sát ngẫu nhiên 36 học sinh tiểu học.
a. Với mức xác suất 90%, thời gian xem TV trung bình của nhóm học sinh này tối thiểu bao nhiêu giờ?
b. Với mức xác suất 95%, thời gian xem TV trung bình của nhóm học sinh này rơi vào trong khoảng nào?
c. Với mức xác suất 99%, độ phân tán về thời gian xem TV của nhóm học sinh này là bao nhiêu giờ?
Giải

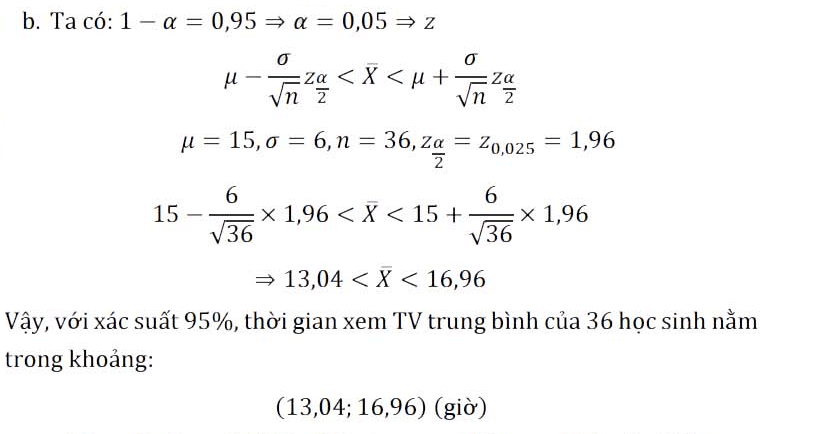
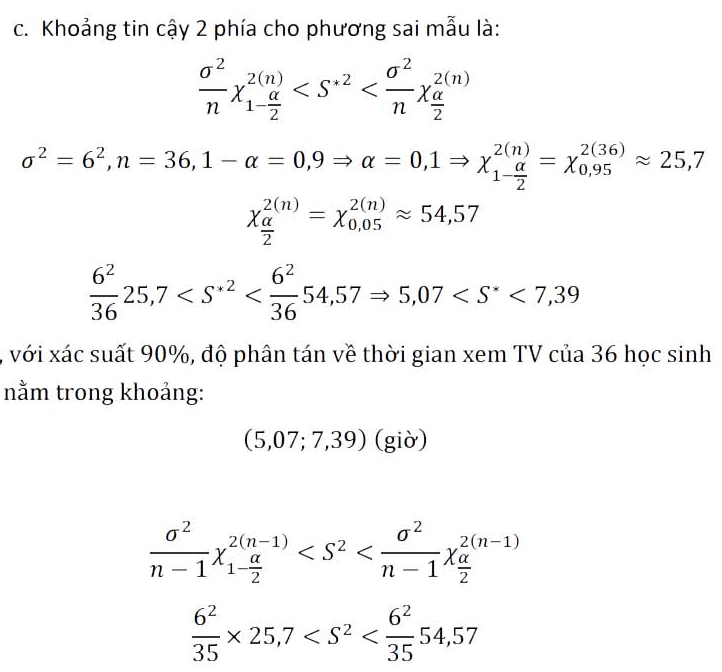
Trên đây là định nghĩa và ví dụ suy đoán về giá trị trung bình, phương sai và tần suất mẫu trong môn xác suất thống kê. Cảm ơn các bạn đã tham khảo trên ttnguyen.net