Ước lượng không chỉ đơn giản là tính toán con số, mà còn đòi hỏi kiến thức sâu rộng về các phương pháp hàm ước lượng. Trong bài viết này, chúng ta sẽ khám phá một chủ đề quan trọng trong lĩnh vực thống kê – ước lượng điểm: tính không chệch và hiệu quả của ước lượng. Ngoài ra, chúng ta cũng sẽ đi sâu vào các phương pháp hàm ước lượng đa dạng mà nhà nghiên cứu và nhà thống kê sử dụng để ước lượng giá trị của các tham số trong một phân phối dữ liệu.
Xem thêm:
I. Phương pháp ước lượng điểm
Là phương pháp dùng một giá trị của thống kê mẫu thay cho một tham số tương ứng chưa biết của tổng thể.
II. Phương pháp hàm ước lượng
Giả sử tổng thể với dấu hiệu nghiên cứu định lượng được đặc trưng bởi biến ngẫu nhiên \(X \sim N(\mu;\sigma^2) \) thì ta cần ước lượng các tham số \(\mu\) và \(\sigma^2\), còn nếu tổng thể với dấu hiệu nghiên cứu định tính được đặc trưng bởi biến ngẫu nhiên \(X \sim A(p) \) thì ta cần ước lượng tham số p.
+ Các tham số \(\mu, \sigma^2, p\) ta họi chung là tham số θ của biến ngẫu nhiên gốc X.
+ Các thống kê \(\overline{X}, S^2, f\) ta gọi chung là các thống kê của mẫu \(\hat{θ}\) của mẫu.
+ Với mẫu ngẫu nhiên \(W_n=(X_1, X_2,…,X_n)\) thì thống kê \(\hat{θ} = f((X_1, X_2,…,X_n))\) là một hàm của các biến ngẫu nhiên nên \(\hat{θ}\) được gọi là hàm ước lượng của θ.
Như vậy:
\(\overline{X}\) là ước lượng điểm của \(\mu\)
\(S^2\) là ước lượng điểm của \(\sigma^2\)
\(f\) là ước lượng điểm của \(p\)
III. Hàm ước lượng
Ước lượng không lệch
Thống kê \(\hat{θ}\) của mẫu được gọi là ước lượng không chênh lệch của tham số θ của biến ngẫu nhiên gốc X nếu:
\(E(\hat{θ}) = θ\)Ngược lại nếu \(E(\hat{θ}) ≠ θ\) thì \(\hat{θ}\) được gọi là ước lượng chệch lệch của θ.
Ước lượng hiệu quả nhất
Thống kê \(\hat{θ}\) của mẫu được gọi là ước lượng hiệu quả nhất của tham số θ của biến ngẫu nhiên gốc X nếu nó là ước lượng không chệch và có phương sai nhỏ nhất so với mọi ước lượng không chệch khác được xây dựng trên cùng mẫu đó.
IV. Bài tập ước lượng điểm
Bài 1: Với mẫu ngẫu nhiên kích thước 3, xét 3 ước lượng cho trung bình tổng thể m sau:
\(G_1 = \frac{X_1 + 2X_2}{2}, G_2=\frac{X_1 + 2X_2 + 3X_3}{6}, \overline{X}\)a. Đâu là ước lượng đủ.
b. Đâu là ước lượng không chênh lệch cho m?
c. Đâu là ước lượng hiểu quả cho m
Giải
a. Ước lượng đủ là sử dụng tất cả các quan sát trong mẫu, do đó: \(G_2, \overline{X}\)
b. Đâu là ước lượng không chênh lệch cho m?

c. Đâu là ước lượng hiểu quả cho m
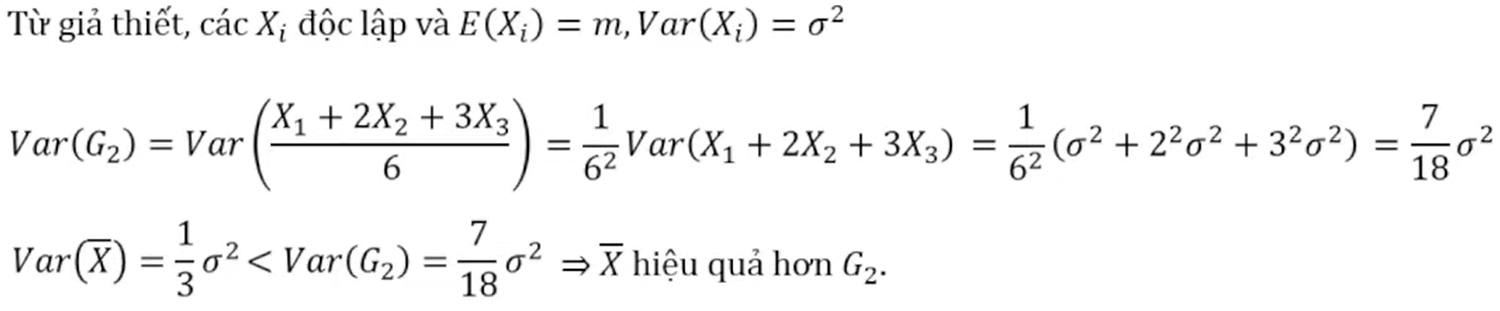
Bài 2: Khi ước lượng cho trung bình tổng thể m, từ hai mẫu ngẫu nhiên độc lập kích thước \(n_1, n_2\)lần lượt lập hai ước lượng \(\overline{X_1}, \overline{X_2}\). Xét các lớp ước lượng tuyến tính \(G_\alpha = \alpha\overline{X_1} + (1-\alpha)\overline{X_2}, 0\le \alpha\le 1\)
a. Chứng minh \(G_\alpha\) bao gồm các ước lượng không lệch cho m?
b. Tìm ước lượng hiểu quả nhất trong \(G_\alpha\)?
Giải
a.
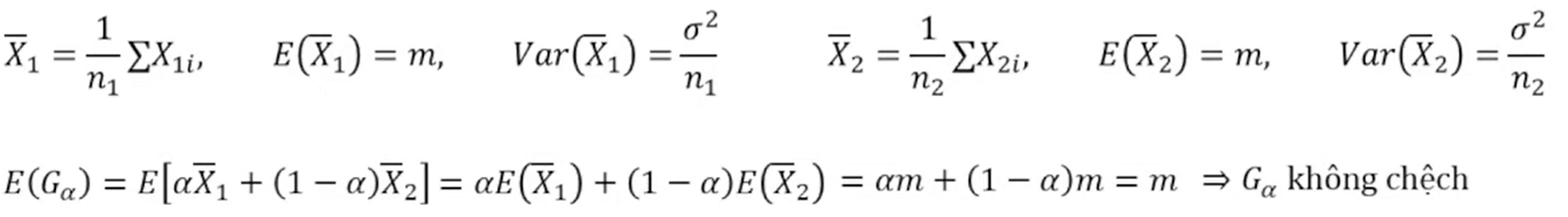
b.

Trên đây là lý thuyết và một vài ví dụ ước lượng điểm có lời giải môn xác suất thống kê. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.