Trong bài viết này, hãy cùng TTnguyen tìm hiểu một số kiến thức cơ bản cùng với các dạng bài tập về ánh xạ tuyến tính thường gặp trong quá trình học đại số và hình học giải tích. Bắt đầu thôi!!!
Xem thêm:
- dạng toàn phương – bài tập đưa về dạng chính tắc
- tìm cơ sở và số chiều của không gian vecto – Bài tập & lời giải
- bài tập không gian eculide kèm lời giải chi tiết
1. Ánh xạ tuyến tính là gì?
Định nghĩa: V→W từ không gian vecto V đến không gian vecto W gọi là ánh xạ tuyến tính nếu thoả mãn 2 tính chất sau:
- f(x,y)=f(x)+f(y)
- f(kx)=kf(x)
∀ x, y∈V, ∀ k∈ R
2. Các tính chất của ánh xạ tuyến tính
Cho V và W là hai không gian véc tơ. Nếu f: V → W là một ánh xạ tuyến tính thì:
- f(θ) = θ
- f(–v) = –f(v), ∀v ∈ V
- f(u – v) = f(u) – f(v), ∀u, v ∈ V.
3. Hạng của ánh xạ tuyến tính – Định lí về số chiều
Định nghĩa hạng của axtt: Nếu f: V → W là một ánh xạ tuyến tính thì số chiều của Im(f) gọi là hạng của f, ký hiệu là rank(f).
rank(f) = dim(Im(f)).
Định lý về số chiều: Nếu f: V → W là một ánh xạ tuyến tính thì
dim(Im(f)) + dim(Ker(f)) = n,
trong đó n = dimV, tức là rank(f) + dim(Ker(f)) = n.
Xem thêm:
- hạng của ma trận
- bài tập tìm cơ sở trực chuẩn và trực giao
3. Chứng minh ánh xạ tuyến tính
Ví dụ: Cho R2→R3, Chứng minh ánh xạ f có phải là ánh xạ tuyến tính hay không?
f(x,y)=(x+y, 0, 2x+2y)
Giải
Lấy 2 vecto bất kỳ thuộc \(R^{2}\): \(x=(a_{1}; b_{1})\) và \(y=(a_{2},b_{2})\)
– \(f(x+y)=(a_{1}+ a_{2},b_{1}+ b_{2})\)
\(= (a_{1} + a_{2} + b_{1} + b_{2}, 0 , 2a_{1} + 2a_{2} + 2b_{1} + 2b_{2})\)
\(= (a_{1} + b_{1} , 0 , 2a_{1} + 2b_{1}) + (a_{2} + b_{2} , 0 , 2a_{2} + 2b_{2}) \)
\(= f(x) + f(y)\)
– \(f (kx) = f(ka_{1} , kb_{1})\)
= \((ka_{1} + kb_{1} , 0 , 2ka_{1} , 2kb_{1})\)
= \(k(a_{1} + b_{1}, 0 , 2a_{1} + 2b_{1})\)
= \(kf(x)\)
Vậy ánh xạ đã cho là ánh xạ tuyến tính.
4. Ma trận của ánh xạ tuyến tính
V là không gian vecto với cơ sở S
W là không gian vecto với cơ sở T
Ma trận của f theo cơ sở S -> T là ma trận gồm các cột là các toạ độ f(s) theo cơ sở T
- Cách tìm ma trận của ánh xạ tuyến tính
- Tìm ảnh f(s)
- Tìm toạ độ \( [f(s)]_{T}\)
5. Cách tìm ma trận chính tắc của ánh xạ tuyến tính
Ví dụ: Tìm ma trận chính tắc của ánh xạ f: R3→R4
f (a, b, c) = (a + b + c, b, bc, a + c)
Giải
Có thể viết lại thành dạng cột:

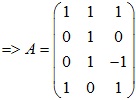
Ví dụ: Tìm ma trận của f theo cơ sở S-T : R3→R2
f (a, b, c) = (b + c, 2a-c)
S = {u 1 (1,0,1), u 2 (4,3,3), u 3 (1,2,1)}
T = {(2,2), (1,7)}
Giải
Tìm ảnh f(s):
f (u 1 ) = f (1,0,1) = (1,1)
f (u 2 ) = f (4,3,3) = (6,5)
f (u 3 ) = (1,2,1) = (3,1)
Tìm toạ độ [f(s)]T
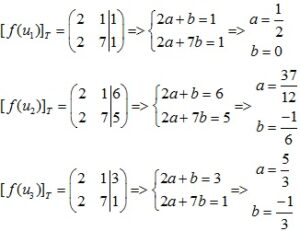
Vậy ma trận S – T là:

Tham khảo:
- bài tập không gian vecto có lời giải
- ứng dụng của đại số tuyến tính trong cuộc sống
6. Bài tập ánh xạ tuyến tính có lời giải
6.1 Bài tập chứng minh ánh xạ tuyến tính có lời giải
Bài 1: Ánh xạ f: R2 → R2 có phải là tuyến tính không?
f (x, y) = (x, y + 1)
Giải
Lấy 2 vecto bất kỳ thuộc \(R^{2}\): \(x=(a_{1}; b_{1})\) và \(y=(a_{2},b_{2})\)
– \(f(x+y)=(a_{1}+ a_{2},b_{1}+ b_{2})\)
= \((a_{1} + a_{2}, b_{1} + b_{2} + 1)\)
= \((a_{1}, b_{1} + 1) + (a_{2} ,b_{2})\)
≠ f (x) + f (y)
Vậy ánh xạ đã cho không phải là ánh xạ tuyến tính.
Bài 2: Ánh xạ f: R2 → R2 có phải là tuyến tính không?
f (x, y) = (y, y)
Giải
Lấy 2 vecto bất kỳ thuộc \(R^{2}\): \(x=(a_{1}; b_{1})\) và \(y=(a_{2},b_{2})\)
– \(f(x+y)=(a_{1}+ a_{2},b_{1}+ b_{2})\)
= \((b_{1}+ b_{2}, b_{1}+ b_{2})\)
= \((b_{1}+ b_{1})+(b_{2}+ b_{2})\)
= \(f (x) + f (y)\)
– \(f (kx) = f(ka_{1} , kb_{1})\)
= \((kb_{1}, ka_{1})\)
= \(k(b_{1}, b_{1})\)
= \(kf(x)\)
Vậy ánh xạ đã cho là ánh xạ tuyến tính.
6.2 Tìm ma trận f đối với cơ sở chính tắc
Bài 1: Tìm ma trận chính tắc của ánh xạ f: R3→R3
f (a, b, c) = (a + 2b + c, a + 5b, c)
Giải
Xem lại ví dụ ở ma trận của ánh xạ tuyến tính ta được ma trận chính tắc là:

Bài 2: Tìm ma trận chính tắc của ánh xạ f sau:
+ f (a, b) = (b, -a, a + 3b, a – b)

+ f (a, b, c, d) = (d, a, c, b, bc)

Bài 3: Tìm ma trận của f theo cơ sở S-T : R2→R3
f (a, b) = (a + 2b, -a, 0)
S = {u 1 (1, 3), u 2 (-2, 4)}
T = {(1, 1, 1), (2, 2, 0), (3, 0, 0)}
Giải
Tìm ảnh của ánh xạ tuyến tính f(s):
f (u 1 ) = f (1,3) = (7, -1 ,0)
f (u 2 ) = f (-2, 4) = (6, 2, 0)
Tìm toạ độ [f(s)]T

Vậy ma trận S – T là:

Bài 4: Xét ánh xạ f: R2 -> R3

 \
\
5. Cho ánh xạ f: P3(x) -> P2(x), p(x) -> p'(x)

6. Tìm một cơ sở cho mỗi không gian Im(f) và ker(f)

Liên quan:
- dạng song tuyến tính – bài tập có lời giải
- căn bậc 2 của số phức
- giải hệ phương trình bằng phương pháp cramer
Tải File bài tập có đáp án tại đây:
Trên đây là toàn bộ kiến thức cơ bản cùng phương pháp giải bài tập ánh xạ tuyến tính trong đại số tuyến tính và hình học. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net