Trong lý thuyết xác suất, bảng phân phối đóng vai trò quan trọng trong việc mô hình hóa dữ liệu. Hai trong số các phân phối quan trọng nhất là phân phối chi bình phương và phân phối gamma. Bài viết dưới đây sẽ cung cấp cho bạn những kiến thức cơ bản cùng với các ví dụ và bài tập thực hành để củng cố những kiến thức đã học.
Xem thêm:
phân phối nhị thức là gì: Công thức và bài tập có lời giải
giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Phân phối chi bình phương là gì?
Phân phối chi bình phương là một phân phối xác suất không âm được sử dụng rộng rãi trong thống kê, đặc biệt là kiểm định giả thuyết và phân tích phương sai.
Biến ngẫu nhiên liên tục X được gọi là có phân phối Chi bình phương, ký hiệu \(X ∼ \chi^2(r)\), nếu hàm mật độ của X có dạng sau:
\(f(x)=\begin{cases}
\frac{1}{\Gamma\left( \frac{r}{2} \right)2^{\frac{r}{2}}}x^{\frac{r}{2}-1}e^{-\frac{x}{2}} \text{ khi } x >0\\
0 \text{ khi } x \le 0
\end{cases}
\)
1.1. Hàm mật độ Chi-Square
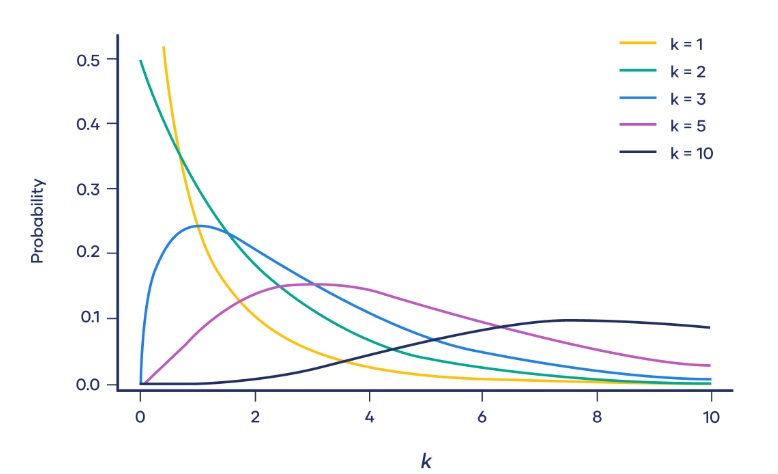
1.2. Trung bình và phương sai Chi-Square
\(\begin{aligned}\text{Trung bình: } \mu_x &= r \\
\text{Phương sai: } \sigma^2_x &= 2r
\end{aligned}\)
Xem thêm:
- phân phối xác suất thành phần – Các đặc trưng và bài tập
- phân phối xác suất có điều kiện và kỳ vọng có điều kiện
2. Phân phối Gramma là gì?
Phân phối gamma là mở rộng khái niệm của phân phối chi bình phương và bao gồm các tham số α và β để xác định hình dạng. Phân phối gamma được ứng dụng trong nhiều lĩnh vực như lý thuyết hàng đợi và phân tích độ tin cậy.
2.1. Hàm Gramma
Hàm Gramma: \(\Gamma: (0, \infty )\to R\)
\(\Gamma(x) = \int_{0}^{\infty}t^{x-1}e^{-t}dt\)Biến ngẫu nhiên liên tục X được gọi là có phân phối Gamma, ký hiệu \(x∼\Gamma(\alpha, \beta)\), với \(alpha, \beta >0\) nếu hàm mật độ của X có dạng sau:
\(f(x)=\begin{cases}
\frac{1}{\Gamma(\alpha)\beta^{\alpha}}x^{\alpha-1}e^{-\frac{x}{\beta}} \text{ khi } x > 0 \\
0 \text{ khi } x \le 0
\end{cases}\)
2.2. Hàm mật độ Gramma
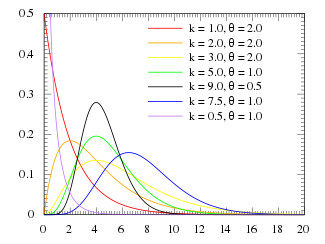
2.3. Trung bình và phương sai Gramma
Cho \(x∼\Gamma(\alpha, \beta)\), ta có:
\(\begin{aligned}\text{Trung bình: } \mu_x &= \alpha \beta \\
\text{Phương sai: } \sigma^2_x &= \alpha \beta^2
\end{aligned}\)
3. Mối liên hệ giữa phân phối chi bình phương và Gramma
Sự liên hệ giữa hai phân phối này là phân phối chi bình phương là trường hợp đặc biệt của phân phối gamma khi \(\alpha=\frac{r}{2}\) và \(\beta=2\)
4. Bài tập phân phối chi bình phương có lời giải
Bài 1: Cho X là đại lượng ngẫu nhiên có hàm mật độ:
\(f(x)=\begin{cases}
\frac{1}{\Gamma\left( \frac{n}{2} \right)2^{\frac{n}{2}}}x^{\frac{n}{2}-1}e^{-\frac{x}{2}} \text{ khi } x >0\\
0 \text{ khi } x \le 0
\end{cases}
\)
trong đó n > 0, được gọi là bậc tự do của phân phối ( X thường được gọi là phân phối chi bình phương với n bậc tự do).
a) Hãy xác định hàm sinh momen của đại lượng ngẫu nhiên X có phân phối chi bình phương với n bậc tự do.
b) Từ kết quả của câu a) Hãy tìm kỳ vọng và phương sai của X.
c) Chứng minh rằng tổng:
\(Z_n=(Y_1)^2+(Y_2)^2+…+(Y_n)^2\)\(Y_i\); i=1,2,…,n là các đại lượng ngẫu nhiên độc lập và có cùng phân phối chuẩn N(0,1), khi đó \(Z_n\) sẽ có phân phối chi bình phương với n bậc tự do.
d) Cho \(X_j\); i=1,2,…,n là các biến ngẫu nhiên độc lập và có phân phối chuẩn tương ứng \(N(m_i, \sigma^2)\). Chứng minh rằng đại lượng \(\eta=\frac{1}{\sigma^2}\sum_{j=1}^{n} X_j^2\) sẽ có phân phối “chi bình phương lệch” với n bậc tự do, nghĩa là nó sẽ có hàm mật độ tương ứng là:
\(\phi_\eta=\frac{1}{2^{\frac{n}{2}}}exp\left( \frac{1}{2}(x+m) \right)x^{\frac{n}{2}-1}\sum_{j=0}^{\infty}\frac{1}{j! \Gamma\left( j+\frac{n}{2} \right)}\left( \frac{mx}{4} \right)^j;x \ge 0\)trong đó: \(m=\frac{1}{\sigma^2}\sum_{j=1}^{n}m_j^2\)
Hãy tìm kỳ vọng và phương sai của phân phối “chi bình phương lệch” với n bậc tự do này.
Giải

5. Bài tập phân phối Gamma
Bài 2: Cho X là đại lượng ngẫu nhiên có hàm mật độ:
\(f(x)=\begin{cases}
\frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}} \text{ khi } x > 0 \\
0 \text{ khi } x \le 0
\end{cases}\)
trong đó \(\alpha > 0, \beta >0 \text{ và } \Gamma(\alpha)\) là hàm Gamma xác định bởi tích phân
\(\Gamma(\alpha) = \int_{0}^{\infty }x^{\alpha-1}e^{-x}dx\)a) Hãy tính các momen gốc cấp n của X.
b) Khi \(\alpha=1, \beta =\lambda >0\), ta có phân phối mũ, với hàm mật độ:
\(f(x)=\begin{cases}
\lambda e^{-\lambda x} \text{ khi } x > 0 \\
0 \text{ khi } x \le 0
\end{cases}\)
Hãy tính kỳ vọng và phương sai của phân phối mũ.
c) Khi \(\alpha=1, \beta = n \in N\), ta có phân phổi Erlang, với hàm mật độ:
\(f(x)=\begin{cases}
ne^{-nx} \text{ khi } x > 0 \\
0 \text{ khi } x \le 0
\end{cases}\)
Hãy tính kỳ vọng và phương sai của phân phối Erlang.
d) Khi \(\alpha= n+1, \beta = 1\), ta có phân phối mũ lũy thừa, với hàm mật độ:
\(f(x)=\begin{cases}
\frac{1}{n!}x^ne^{-e} \text{ khi } x > 0 \\
0 \text{ khi } x \le 0
\end{cases}\)
Hãy tính kỳ vọng và phương sai của phân phối mũ lũy thừa.
Giải

Tài liệu PDF liên quan:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Hy vọng qua các bài tập đã đưa ra, bạn sẽ nắm vững hơn kiến thức về bảng phân phối chi bình phương và gamma. Cảm ơn bạn đã tham khảo trên ttnguyen.net.
Bài viết liên quan:
phân phối đều là gì? Công thức và bài tập có lời giải
phân phối siêu bội – Công thức và bài tập có lời giải
phân phối Fisher – snedecor | Cách tra bảng đầy đủ PDF
giáo trình xác suất thống kê PDF