Trong môn đại số và hình học giải tích, ma trận chuyển cơ sở là một khái niệm quan trọng . Nó được sử dụng để mô tả một phép biến đổi tuyến tính giữa hai không gian vector có cùng số chiều với nhau. Sau đây, hãy cùng ttnguyen.net tìm hiểu định nghĩa và bài tập và cách tìm ma trận chuyển cơ sở nhé!!!
Xem thêm:
I. Định nghĩa ma trận chuyển cơ sở
Ma trận chuyển cơ sở là ma trận chuyển đổi tọa độ của một vectơ từ cơ sở này sang cơ sở khác.. Ma trận chuyển S→T là ma trận toạ độ của T theo S.
II. Cách tìm ma trận chuyển cơ sở
Muốn tìm ma trận chuyển cơ sở từ S sang T, kí hiệu P(S→T), ta cần tìm tọa độ của các vector trong cơ sở T đối với cơ sở S, sau đó viết ma trận theo quy tắc, mỗi tọa độ là một cột của ma trận theo thứ tự.
Ngược lại, muốn tìm ma trận chuyển cơ sở từ T sang S, kí hiệu P(T→S), ta cần tìm tọa độ của các vector trong S đối với cơ sở T và viết ma trận theo quy tắc trên.
Ví dụ: Trong không gian \(R^{3}\) cho 2 hệ cơ sở:
\(S={u_{1}(1,1,1) , u_{2}(1,0,2), u_{3}(1,2,1)}\) \(T={v_{1}(2,3,2) , v_{2}(-1,1,4), v_{3}(2,1,3)}\)Tìm ma trận chuyển cơ sở từ S sang T.
Giải
Xét ma trận sau:
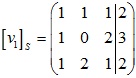
Giải hệ phương trình:
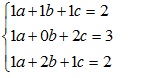
ta được 3 nghiệm a=1,b=0,c=1.
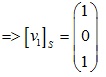
Tương tự xét ma trận:
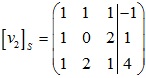
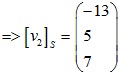
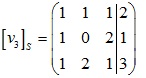
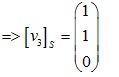
Vậy ma trận cần tìm là:
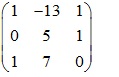
Xem thêm:
- hệ phương trình tuyến tính – Bài tập có lời giải PP Gauss
- chéo hoá ma trận
- ánh xạ tuyến tính
III. Bài tập ma trận chuyển cơ sở
1. Tìm ma trận chuyển cơ sở từ u sang v
Bài toán: Xét không gian \(R^{3}\) với 2 cơ sở:
\(u_{1}(1,0,0); u_{2}(0,1,0); u_{3}(0,0,1) và v_{1}(1,1,0); v_{2}(0,1,1); v_{3}(1,0,1)\)a) Tìm ma trận chuyển từ cơ sở (u) sang cơ sở (v)
b) Tìm ma trận chuyển từ cơ sở (v) sang cơ sở (u)
Hướng dẫn giải
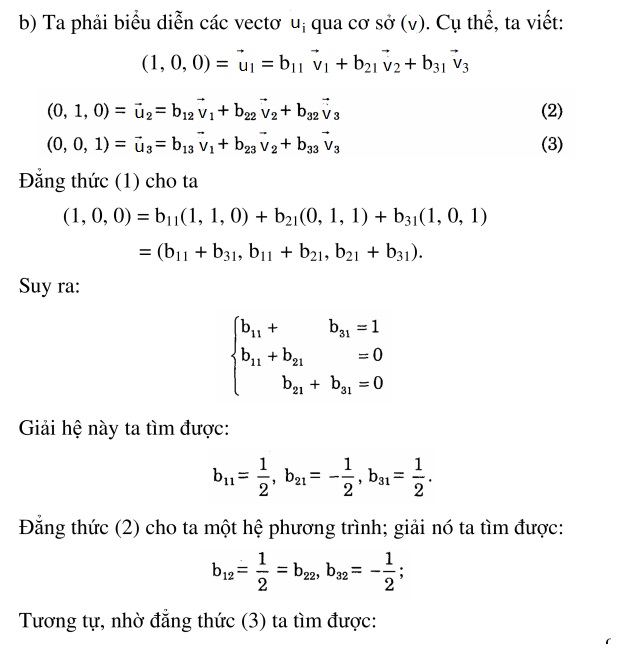
2. Ma trận chuyển từ cơ sở u sang cơ sở v là
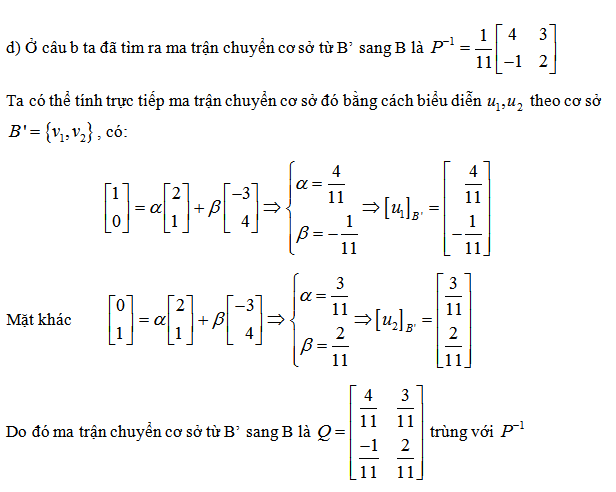
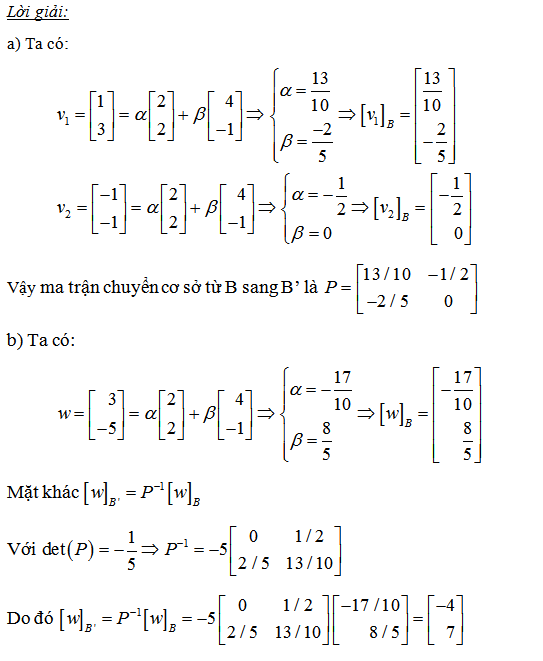
3. Tìm ma trận chuyển cơ sở
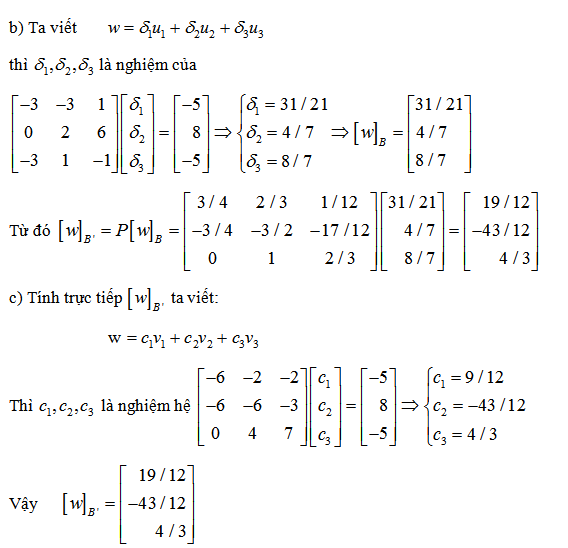
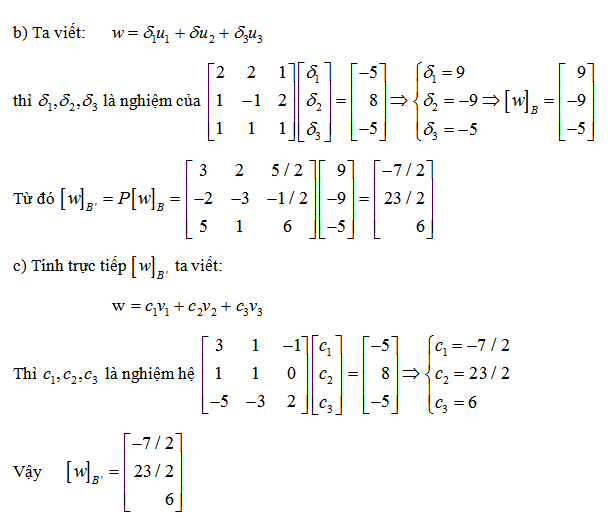
4. Tìm ma trận chuyển cơ sở từ u sang v
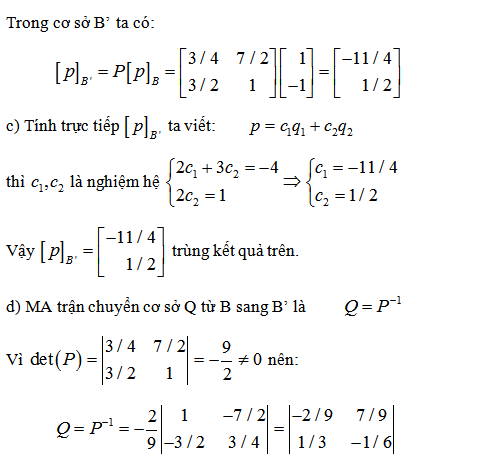
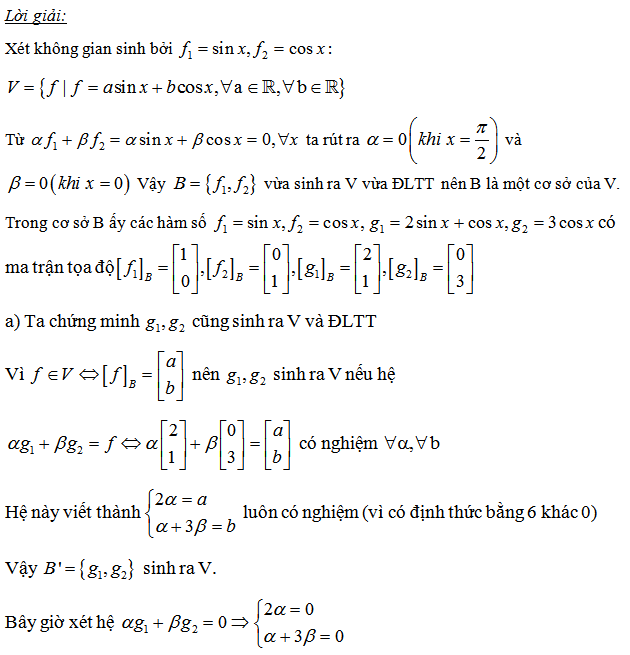
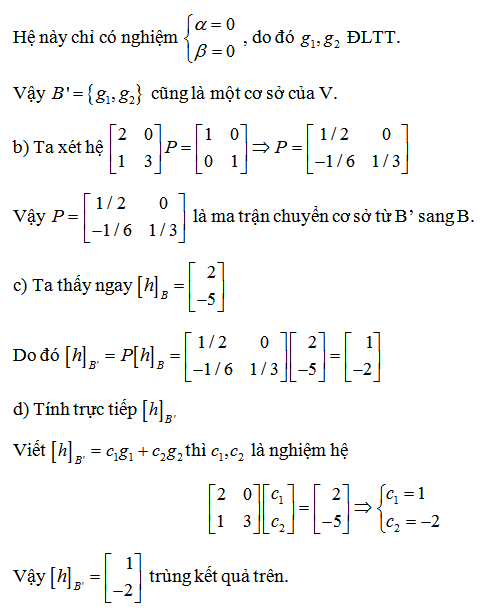
Tài liệu ma trận chuyển cơ sở PDF:
Trong bài viết này, chúng ta đã tìm hiểu về khái niệm và cách tìm ma trận chuyển cơ sở. Hi vọng các bạn đã có cái nhìn tổng quan và có thể thực hiện các bài tập liên quan. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Bài viết liên quan:
