Đại số ma trận được nghiên cứu và phát triển một cách hệ thống vào năm 1858 bởi Arthur Cayley đem đến nhiều ứng dụng hữu ích. Bài viết dưới đây TTnguyen sẽ chia sẻ kiến thức cơ bản cùng các dạng bài tập ma trận có lời giải chi tiết giúp các bạn ôn tập dễ dàng. Bắt đầu thôi!
Xem thêm:
1. Ma trận là gì toán cao cấp?
Ma trận là một mảng hai chiều các số được sắp xếp thành các hàng và cột. Mỗi phần tử trong ma trận được định vị bằng một cặp chỉ số, thường là số nguyên không âm, một chỉ số dùng để xác định hàng và một chỉ số khác dùng để xác định cột. Ma trận thường được ký hiệu bằng chữ cái in hoa: A,B,C.
- Ma trận cỡ m x n là 1 bảng số hình chữ nhật gồm m hàng, n cột.
- Kí hiệu ma trận : A = (aij) m x n.
- Ví dụ dưới đây là một ma trận:
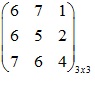
Ma trận mxn
Ma trận có nhiều hình dạng khác nhau tuỳ thuộc vào số hàng và cột. Thường thì ma trận với m hàng và n cột thường được gọi là ma trận m x n. Với ma trận có kích thước 1 x n được gọi là ma trận hàng, ma trận có kích thước m x 1 được gọi là ma trận cột. Ma trận cỡ n x n được gọi là ma trận vuông.
Với ma trận A là ma trận 3×4 có aij. Thì ma trận A được biểu thị như sau:

Tóm lại:
- Nếu ma trận cỡ m x n, thì nó có m hàng và n cột.
- Phần tử ma trận aij nghĩa là phần tử nằm ở hàng i cột j.
Ma trận cấp 2
Một ma trận cấp 2 là một ma trận có kích thước 2 hàng và 2 cột. Dưới đây là một ví dụ về ma trận cấp 2:
\(\begin{vmatrix}1 & 2\\
4 & 5
\end{vmatrix}\)
Liên quan:
2. Các dạng ma trận
Ma trận 0
Ma trận 0 là các phần tử đều bằng 0.
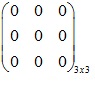
Ma trận đường chéo
Ma trận đường chéo là ma trận vuông mà các phần tử ngoài đường chéo chính bằng 0.

Ma trận đơn vị
Ma trận đơn vị là ma trận có các phần tử đường chéo bằng 1.
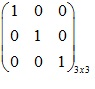
Ma trận tam giác trên
Ma trận tam giác trên là ma trận vuông mà các phần tử nằm dưới đường chéo chính bằng 0.

Lưu ý: Nếu ma trận có đường chéo chính bằng 0, nó được gọi là ma trận tam giác trên.
Ví dụ:
\(\begin{vmatrix}0 & 2& 3\\
0 & 0& 0\\
0 & 0& 0
\end{vmatrix}\)
Ma trận tam giác dưới
Một ma trận tam giác dưới là một ma trận trong đó tất cả các phần tử nằm trên đường chéo chính và trên đường chéo chính đều bằng 0. Các phần tử trên đường chéo chính có thể là 0 hoặc khác 0. Dưới đây là một ví dụ về ma trận tam giác dưới:
\(\begin{vmatrix}1 & 0& 0\\
2 & 3& 0\\
4 & 5& 6
\end{vmatrix}\)
Trong ví dụ này, các phần tử nằm trên đường chéo chính và trên đường chéo chính đều bằng 0, và các phần tử còn lại có thể là bất kỳ giá trị nào. Ma trận tam giác dưới có dạng tam giác với các phần tử khác 0 chỉ nằm dưới đường chéo chính.
Ma trận chuyển vị của A
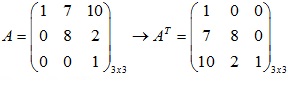
Ma trận bậc thang
- Nếu các hàng = 0 thì phải ở dưới cùng
- Nếu các hàng ≠ 0 thì phần tử đầu tiên của hàng dưới phải lệch sang phải phần tử ≠ 0 đầu tiên hàng trên

Xem thêm:
- ma trận bậc thang
- ma trận kề – biểu diễn đồ thị, danh sách kề
3. Các tính chất của ma trận
Giả sử A,B,C là các ma trận cùng cỡ, k,t là các số thực bất kỳ. Khi đó:
- A+B = B+A
- (A+B)+C = A+ (B+C)
- A+0 = 0+A = A
- A+(-A) = (-A)+A=0
- k(A+B)=kA+kB
- (k+t)A = kA+tA
- k(tA) = kt(A)
- 1.A=A
- 0.A=0
- A(B+C) = AB+AC
- (A+B)C = AC+BC
- (kA)B = A(kB) = k(AB)
- AI=IA=A
- (AB)T = BT.AT
4. Các phép toán ma trận
Các phép toán trên ma trận là quá trình thực hiện các phép tính số học và đại số trên các phần tử của ma trận. Dưới đây là một số phép toán cơ bản trên ma trận:
2 ma trận bằng nhau
Hai ma trận gọi là bằng nhau nếu chúng cùng cỡ (cùng cấp) và các phần tử tƣơng ứng ở cùng vị trí thì bằng nhau
Ví dụ về 2 ma trận bằng nhau là:
Ma trận A:
\(\begin{vmatrix}1 & 2& 3\\
4 & 5& 6\\
7 & 8& 9
\end{vmatrix}\)
Ma trận B:
\(\begin{vmatrix}1 & 2& 3\\
4 & 5& 6\\
7 & 8& 9
\end{vmatrix}\)
Ma trận A và ma trận B có cùng kích thước là 3 hàng và 3 cột và các phần tử trong cùng vị trí của hai ma trận này đều giống nhau. Do đó, ta có thể nói rằng hai ma trận A và B là bằng nhau.
Phép cộng 2 ma trận
Để cộng hai ma trận cùng kích thước, bạn chỉ cần cộng từng phần tử tương ứng của hai ma trận lại với nhau. Cụ thể, các bước để cộng hai ma trận như sau:
Điều kiện cộng 2 ma trận:
Đảm bảo rằng hai ma trận có cùng kích thước (cùng số hàng và số cột).
cách cộng 2 ma trận
Cộng từng phần tử tương ứng của hai ma trận lại với nhau. Điều này có nghĩa là phần tử ở hàng i, cột j của ma trận kết quả sẽ là tổng của phần tử ở hàng i, cột j của ma trận thứ nhất và phần tử ở hàng i, cột j của ma trận thứ hai.
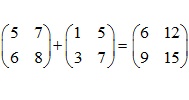
Lưu ý: Không cộng 2 ma trận không cùng cấp.
Tính chất:
- Với A, B, C là ma trận bất kỳ cùng cỡ thì: A+B = B+A ; A+(B+C) = (A+B)+C
- Ma trận nào cộng với ma trận không cũng bằng chính nó: 0+X=X
- Phép trừ ma trận: A-B được xác định bởi: A-B=A+(-B)
Ví dụ 1: Tính -A, A-B và A+B-C các ma trận sau:
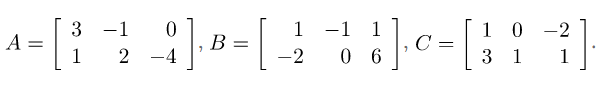

Ví dụ 2: Tìm ma trận X sau:
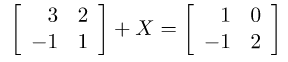
Giải
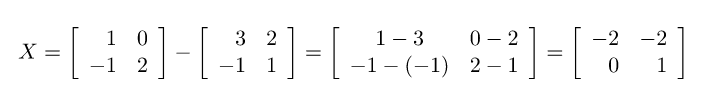
Phép trừ 2 ma trận
Để trừ hai ma trận cùng kích thước, bạn cần trừ từng phần tử tương ứng của hai ma trận lại với nhau. Cụ thể, các bước để trừ hai ma trận như sau:
Bước 1: Đảm bảo rằng hai ma trận có cùng kích thước (cùng số hàng và số cột).
Bước 2: Trừ từng phần tử tương ứng của hai ma trận.
Bước 3: Ghi lại kết quả vào ma trận kết quả.
Dưới đây là một ví dụ cụ thể về phép trừ hai ma trận:
Ma trận A:
\(\begin{vmatrix}5 & 8\\
3 & 2
\end{vmatrix}\)
Ma trận B:
\(\begin{vmatrix}2 & 4\\
1 & 1
\end{vmatrix}\)
Bước 1: Xác định hai ma trận có cùng kích thước (2 hàng, 2 cột).
Bước 2: Trừ từng phần tử tương ứng của hai ma trận:
5 – 2 = 3; 8 – 4 = 4
3 – 1 = 2; 2 – 1 = 1
Ma trận kết quả:
\(\begin{vmatrix}3 & 4\\
2 & 1
\end{vmatrix}\)
Lưu ý:
- Không trừ ma trận với 1 số
Xem thêm:
nhân 2 ma trận – Điều kiện và cách tính có lời giải
Các dạng bài tập ma trận và cách giải
1.Tìm ma trận x thoả mãn:
a/
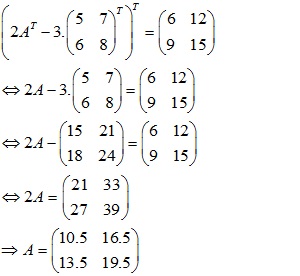
b/
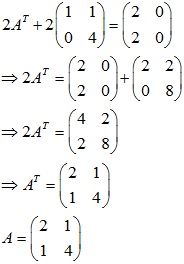
c/ Tìm a thoả mãn:


d/Tìm a thoả mãn ma trận

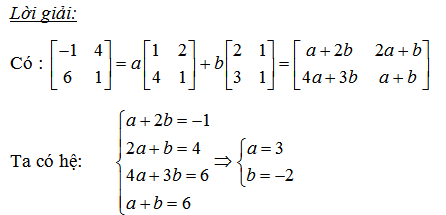
2. Chứng minh ma trận

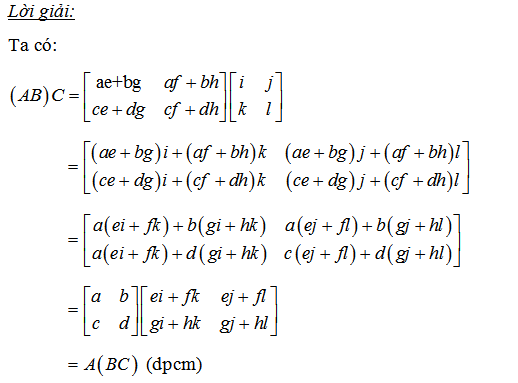
3. So sánh ma trận AB,BA

Để so sánh hai ma trận AB và BA, ta cần tính toán kết quả của phép nhân hai ma trận đó.
Ma trận AB:
\(\begin{vmatrix}1*4+2*2 & 1*3+2*1\\
3*4+4*2 & 3*3+4*1
\end{vmatrix}\)
= \(\begin{vmatrix}
8 & 5\\
20 & 13
\end{vmatrix}\)
Ma trận BA:
\(\begin{vmatrix}4*1+3*3 & 4*2+3*4\\
2*1+1*3 & 2*2+1*4
\end{vmatrix}\)
= \(\begin{vmatrix}
13& 20\\
5 & 8
\end{vmatrix}\)
Kết quả cho thấy AB và BA không bằng nhau.
3. Bài tập ma trận bậc thang có lời giải
Ví dụ: Đưa ma trận sau về ma trận bậc thang:
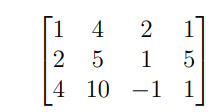
Hướng dẫn giải

Như vậy ta đã hoàn thành đưa ma trận về dạng ma trận bậc thang
Bài viết liên quan:
Tải file bài tập về ma trận và lý thuyết ma trận có lời giải PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Hi vọng qua bài viết trên các bạn đã nắm vững kiến thức cơ bản và biết cách giải ma trận theo yêu cầu bài toán môn đại số và hình giải tích. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net