Tổng hợp kiến thức cơ bản cùng các dạng bài tập hạng của ma trận thường gặp trong môn đại số và hình học giải tích giúp các bạn ôn tập dễ dàng hơn.
Xem thêm:
I. Hạng của ma trận là gì?
Định nghĩa
Hạng của ma trận là số lượng lớn nhất của cột hoặc hàng độc lập tuyến tính của ma trận. Hay hiểu nôm na là số lượng hàng khác không.
Lưu ý: Hạng của ma trận không thể vượt quá số hàng hoặc số cột của ma trận.
Ký hiệu hạng của ma trận: rank(A), r(A)
Ma trận rỗng không có hàng hoặc cột nào khác không. Vì vậy, không có hàng hoặc cột độc lập. Do đó hạng của ma trận rỗng bằng không.
- Ví dụ: Tìm rank của ma trận sau:
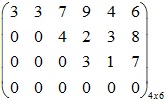
Giải
Xác định cấp của ma trận: Vì ma trận cỡ 4×6 nên có các định thức ma trận con cấp 1,2,3,4
Xét det(4)
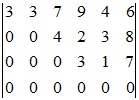
Định thức =0 vì có 1 hàng bằng 0 => Loại
Xét det(3) (Lấy bất kỳ)
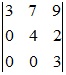
det=3.4.3=36 ≠0
Vậy hạng của ma trận bằng 3
=> hạng của ma trận bậc thang chính là số hàng ≠ 0
II. Phương pháp tìm hạng của ma trận
Để tìm hạng của ma trận, chúng ta thực hiện qua 2 bước sau:
- Bước 1: Đưa ma trận cần tìm về dạng bậc thang bằng phương pháp biến đổi siêu cấp trên hàng và cột
- Bước 2: Số hàng khác 0 của ma trận bậc thang chính là hạng của ma trận đã cho.
Xem thêm:
Ví dụ cách tìm hạng của ma trận:
– Ví dụ 1: Tìm hạng của ma trận sau:
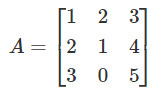
Giải
Số hàng khác 0 là 2. Vậy hạng của ma trận là 2
– Ví dụ 2: Tìm hạng của ma trận sau:
Giải
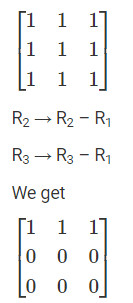
Số hàng khác 0 là 1. Vậy hạng của ma trận là 1
Bài viết liên quan
- bài tập và cách tìm ma trận chuyển cơ sở
III. Bài tập tìm hạng của ma trận
1.Tìm hạng của ma trận 4×4
Bài 1: Tìm hạng của ma trận 4×4
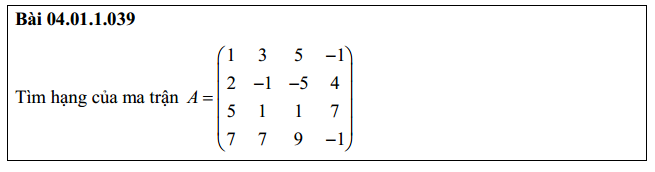
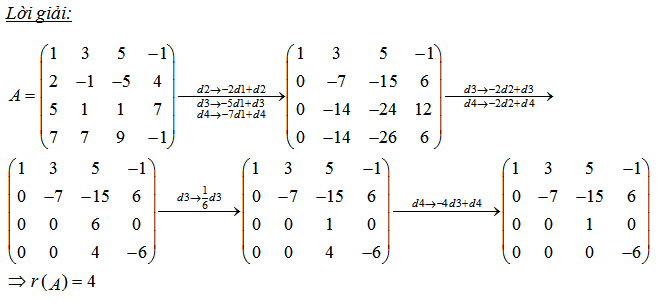
Bài 2: Tìm hạng của ma trận cấp 4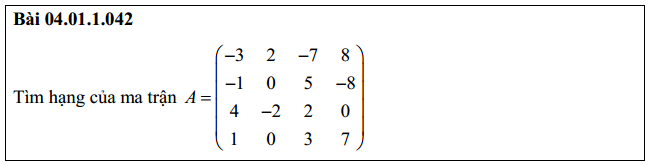 
Bài 3: Tìm hạng của ma trận cấp 4 sau:
Giải
-Chuyển về ma trận bậc thang
-Đổi chỗ hàng 1 và 2 để tính toán dễ dàng hơn
Có 2 hàng ≠0 nên rank(A) =2
2. Tìm hạng của ma trận
Bài 1: Tìm hạng ma trận
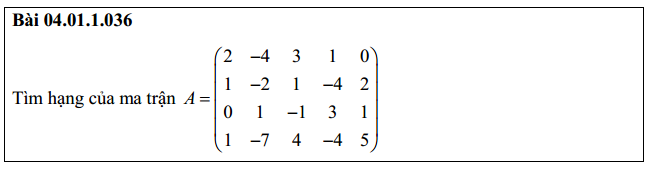
Bài 2: tìm rank của ma trận
Bài 3: tính hạng của ma trận
Bài 4: tính hạng ma trận
Bài 5: tính rank ma trận
Bài 6: xác định hạng của ma trận
Xem thêm:
3. Biện luận hạng ma trận theo theo tham số m
Bài 1: biện luận theo m hạng của ma trận
Bài 2: tìm hạng ma trận theo m
Bài 3: giải và biện luận ma trận theo tham số m
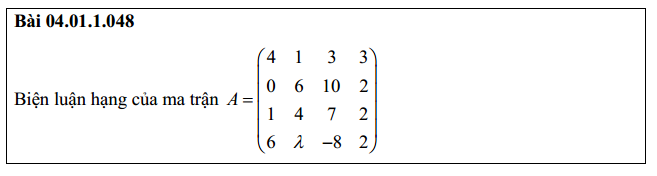
Bài 4: tìm hạng của ma trận có chứa tham số
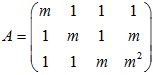
Giải
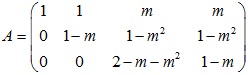
cho 1-m=0, 2-m-m2 =0 ta được 2 nghiệm m=1 và m=-2
+Với m=1
=> rank(A)=1
+ Với m=-2
=> rank(A)=3
+Với m≠1,-2 => rank(A)=3
Bài 5: Tìm hạng của ma trận theo m
Giải
Biến đổi ma trận về ma trận tam giác trên
Cho -m2-3m+4=0 ta đc 2 nghiệm m=-4; m=1
+Với m=1, 3m+2≠0
=> Vậy với m=1,3m+2≠0 thì hạng ma trận là 3
+Với m=-4
Vậy với m=-4,3m+2≠0 thì hạng ma trận là 4
Vậy với m ≠1, m≠-4,3m+2≠0 thì hạng ma trận là 4
Bài 6: biện luận theo tham số m hạng của ma trận
Giải
Đổi vị trí cột 1 và 4 để dễ tính hơn
Biến đổi về ma trận tam giác trên
Vậy với m =0 thì rank=2; m≠0 thì rank =3
Bài 7: giải và biện luận ma trận theo tham số m
Giải
Đổi cho để thuận tiện cho việc tính toán
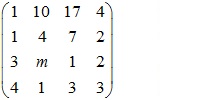
Biến đổi về ma trận tam giác trên
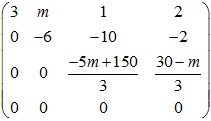
+Với -5m+150=0 => hạng ma trận là 2
+Với -5m+150≠0 => hạng ma trận là 3
4. Tìm m để hạng ma trận bằng 2
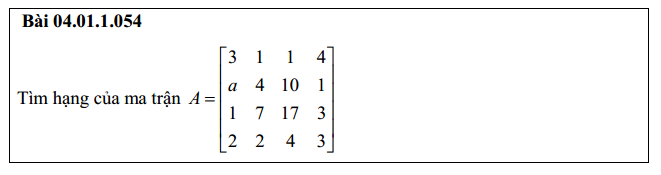
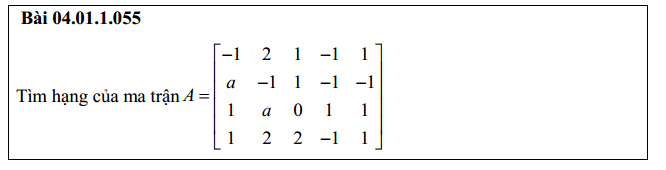
5. Tìm m để hạng ma trận bằng 3
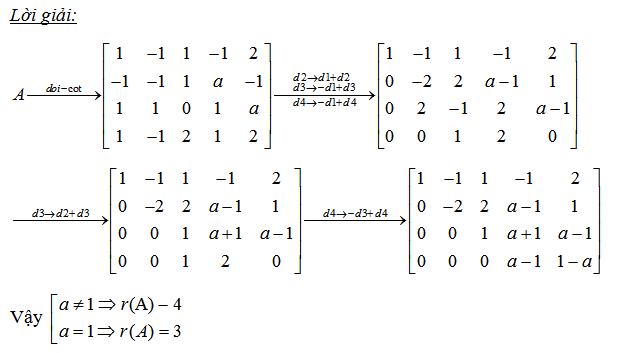
Tải File lý thuyết hạng của ma trận kèm bài tập vận dụng, trắc nghiệm tất tần tật PDF:
Như vậy, qua bài viết trên hi vọng bạn đã biết cách tìm hạng của ma trận, tìm rank của ma trận và nắm vững kiến thức cơ bản giúp bạn giải quyết được các bài toán về hạng của ma trận. Cảm ơn bạn đã tham khảo tài liệu trên ttnguyen.net!
