Chéo hoá ma trận – Bài tập và phương pháp có lời giải

Trong đại số và hình học giải tích, chéo hoá ma trận là quá trình tìm ma trận nghịch đảo T và ma trận chéo B. Các ma trận chéo hóa rất dễ tính toán, sau khi đã tìm được các giá trị riêng và vectơ riêng của chúng. Bài viết dưới đây sẽ giúp các bạn hiểu rõ hơn định nghĩa, điều kiện và cách giải bài tập về chéo hoá ma trận.

Xem thêm:

• ánh xạ tuyến tính
• bài tập tìm cơ sở trực chuẩn và trực giao
• dạng lượng giác của số phức

I. Chéo hoá ma trận là gì?

Định nghĩa

Ma trận gọi là ma trận chéo hoá nếu tồn tại ma trận khả nghịch T sao cho \(B= T^{-1}AT\) với B là một ma trận chéo. Khi đó ta nói ma trận T làm chéo hoá A và B là dạng chéo của A. Như vậy, chéo hoá ma trận A là tìm ra ma trận khả nghịch T và ma trận chéo B.

Với \(A= TBT^{-1}\) thì khi đó nếu cần tính \(A^{n}\):

Ta có: \(A^{n} = (TBT^{-1})^{n} = TB^{n}T^{-1}\)

II. Điều kiện chéo hoá ma trận

Ma trận A chéo hoá được khi và chỉ khi thoả mãn các tính chất sau:

• Điều kiện cần và đủ để ma trận A chéo hoá được là nó có n vecto riêng độc lập tuyến tính.
• Đa thức đặc trưng det(A – λI) phân tích được thành các đa thức bậc 1.
• Nếu ma trận A có n trị riêng đôi một khác nhau thì A chéo hóa được.

II. Cách chéo hoá ma trận

Bước 1: Giải phương trình det(A – λI) = 0 để tìm các trị riêng.

Bước 2: giải hệ (A – λI)X = 0 Nếu có đủ n véc tơ riêng độc lập tuyến tính thì ma trận A chéo hóa được.

Bước 3: Lập ma trận T

Bước 4: Ma trận T^-1AT là ma trận đường chéo đồng dạng với ma trận A

Xem thêm:

• định thức ma trận
• bài tập không gian eculide

IV. Ví dụ về chéo hoá ma trận 3×3

Ví dụ chéo hoá ma trận 3×3 sau:

Giải

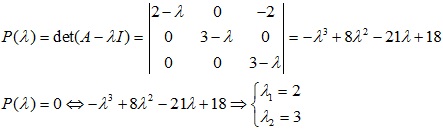
Vậy λ₁ = 2 và λ₂ = 3 và các giá trị riêng

Vậy vector riêng ứng với λ₁ = 2 là {t (1,0,0), t∈R}

\

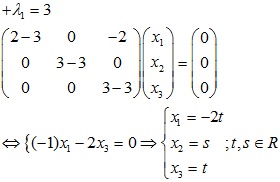Vậy vector riêng ứng với λ₂ = 3 là {s (0,1,0) + t(-2,0,1), t, s ∈R}

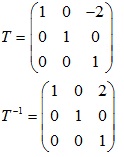
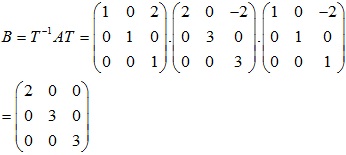
Giải bài tập về chéo hoá ma trận

Bài 1: Các ma trận sau đây có chéo hoá được không?

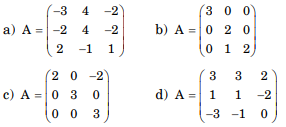
Giải

Bài 2: Chéo hoá ma trận \(A=\begin{pmatrix}
0 & 0& 1\\
0 & 1& 0\\
1 & 0& 0
\end{pmatrix}\)

Giải

3.Tìm ma trận khả đảo T sao cho T ^-1AT là ma trận chéo trong đó

Trên đây là một số bài tập về chéo hoá ma trận. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.

Tài liệu chéo hóa ma trận PDF:

Bài viết liên quan:

• bài tập matlab có lời giải
• ứng dụng của đại số tuyến tính trong cuộc sống nhé!
• bài tập dạng toàn phương có lời giải
• dạng song tuyến tính