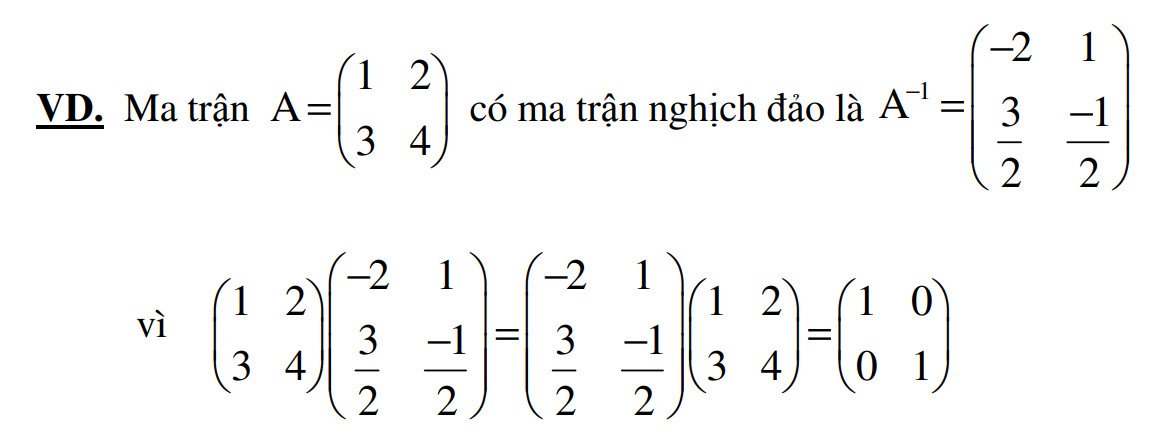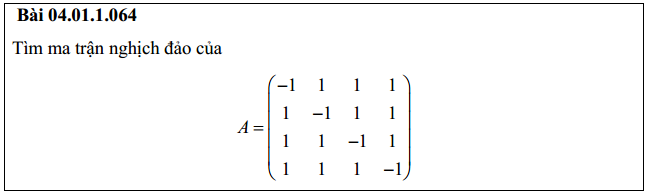Ma trận nghịch đảo là một khái niệm quan trọng trong đại số và hình học giải tích và có ứng dụng rộng trong nhiều lĩnh vực. Bài viết này, ttnguyen.net sẽ hướng dẫn các bạn cách tìm ma trận nghịch đảo 3×3 qua bài tập chi tiết.
Xem thêm:
I. Ma trận nghịch đảo
1. Ma trận nghịch đảo là gì?
Một ma trận A được coi là khả nghịch nếu tồn tại một ma trận B sao cho tích của A và B bằng ma trận đơn vị (ma trận có các phần tử trên đường chéo chính bằng 1 và các phần tử còn lại bằng 0). Ma trận B trong trường hợp này được gọi là ma trận nghịch đảo của A và ký hiệu là \(A^{-1}\).
Nói cách khác:
- Ma trận \(A^{-1}\) gọi là ma trận nghịch đảo của A nếu: \(A.A^{-1}=A^{-1}.A=I\) với I là một ma trận đơn vị
- Ký hiệu ma trận nghịch đảo của A là : \(A^{-1}\)
2. Ví dụ ma trận nghịch đảo
II. Tính chất của ma trận nghịch đảo
Một vài tính chất quan trọng của ma trận nghịch đảo được liệt kê dưới đây:
- \(A^{-1}\) là duy nhất
- \((A^{-1})^{-1}=A\)
- \((A^{-1}.B^{-1})=B^{-1}.A^{-1}\)
- \(X.A=B \Rightarrow X=B.A^{-1} \)
- \(A.X=B \Rightarrow X=A^{-1}.B\)
- \(A.X.B=C ⇒ X=A^{-1}.C.B^{-1}\)
III. Điều kiện tồn tại ma trận nghịch đảo
Để một ma trận có ma trận nghịch đảo, điều kiện cần và đủ là định thức ma trận đó khác 0. Điều này được viết dưới dạng công thức toán học như sau:
det(A) ≠ 0. Trong đó, det(A) là định thức của ma trận A.
Nếu định thức của ma trận bằng 0 (det(A) = 0), tức là ma trận không có ma trận nghịch đảo.
IV. Cách tìm ma trận nghịch đảo
1. Cách tìm ma trận nghịch đảo 2×2
Với ma trận 2×2, ta có thể tìm ma trận nghịch đảo bằng công thức đơn giản sau:
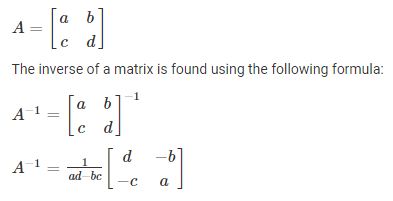
2. Cách tìm ma trận nghịch đảo 3×3, 4×4
- Bước 1: Tính det A. Nếu det A ≠ 0 thì tồn tại ma trận nghịch đảo và ngược lại nếu A=0 thì không tồn tại ma trận nghịch đảo
- Bước 2: Áp dụng công thức tính ma trận nghịch đảo
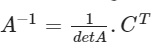 với A là một ma trận, detA: định thức của A; CT là ma trận chuyển vị
với A là một ma trận, detA: định thức của A; CT là ma trận chuyển vị
Đọc thêm: giáo trình đại số tuyến tính
V. Bài tập ma trận nghịch đảo có lời giải
Bài 1: Tìm ma trận nghịch đảo của A

Giải
detA = (1.3.2 + 1.2.3 + 1.2.3) – (3.3.3 + 1.1.1 + 2.2.2) = 18 – 34 = -18 ≠0
Viết công thức và thực hiện đan dấu như hình dưới:
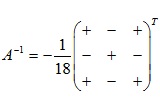
Đối với phần tử a11 ta loại bỏ hàng 1 và cột 1 của ma trận A
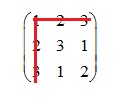
Sau khi loại bỏ ta được như hình dưới
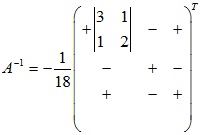
Đối với a12 thì loại bỏ hàng 1 cột 2
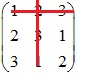
Tương tự đối với các phần tử còn lại ta được:
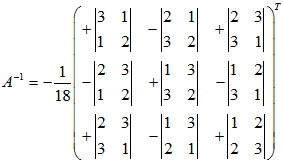
Tính định thức ta được:
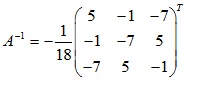
Chuyển vị và ta được kết quả cuối cùng:
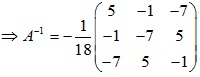
Luyện tập trắc nghiệm: trắc nghiệm đại số tuyến tính có đáp án
Bài 2: Tìm nghịch đảo của ma trận
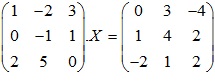
Giải
Ta có: \(A.X=B ⇒ X=A^{-1}.B\)
det A = (1.-1.0 + 0.5.3 + -2.2.1) – (2.-1.3 + 1.1.5 + 0.0.-2) = -3≠0

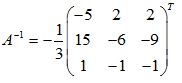
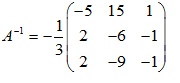
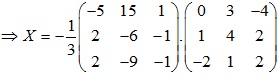
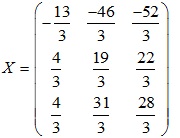
Bài 3: Tìm nghịch đảo của ma trận

Giải
Ma trận khả nghịch khi det(A) ≠ 0
=> det(A)=-4+8-(2-12)=14 ≠ 0 Vậy ma trận khả nghịch.
Tìm ma trận nghịch đảo A-1

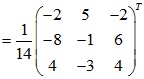
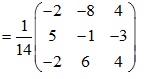
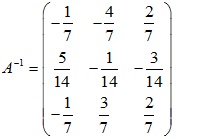
Vậy
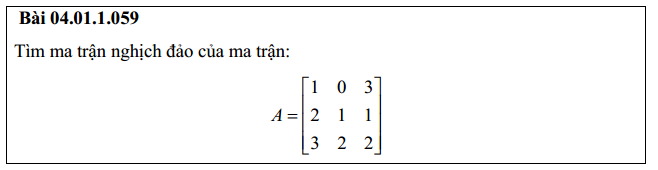


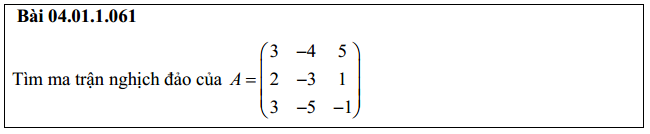
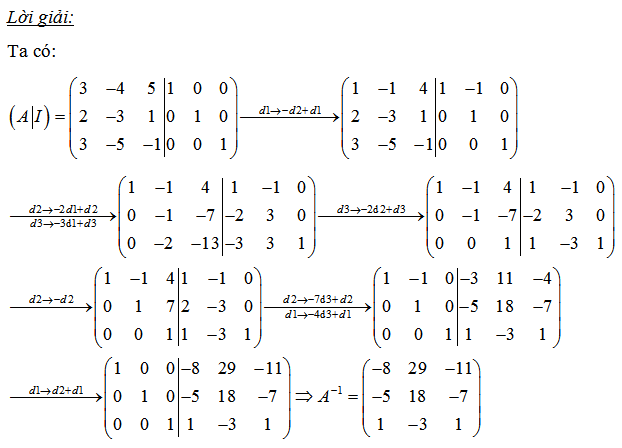
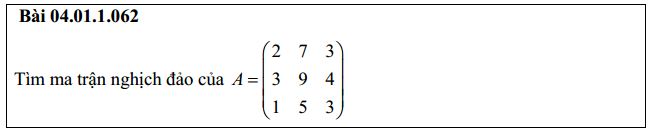

Bài 4: Tìm ma trận nghịch đảo 4×4

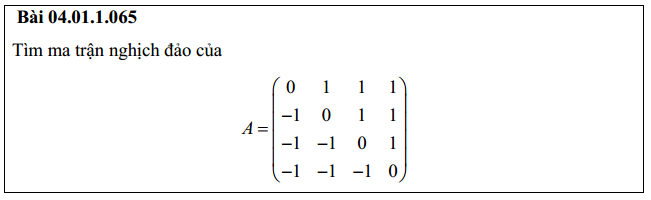
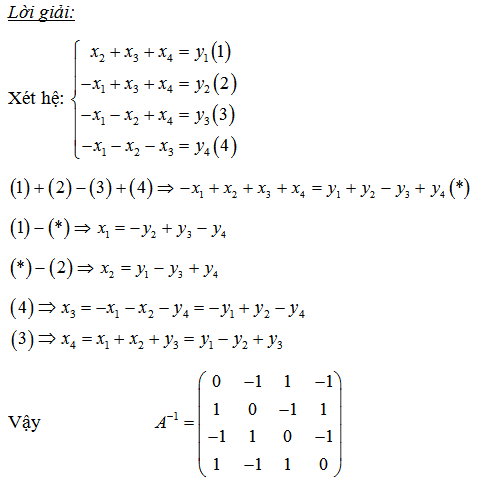
Bài 5: Tìm ma trận nghịch đảo của ma trận nxn
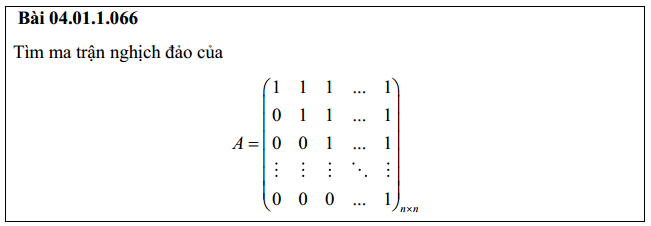
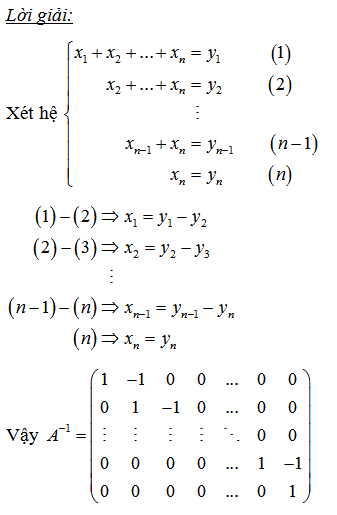


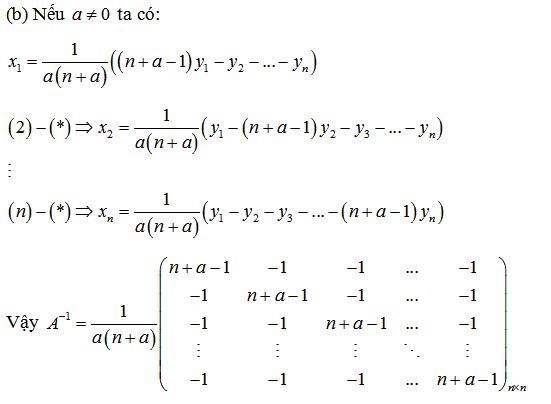
VI. Tìm m để ma trận khả nghịch
Điều kiện để ma trận khả nghịch
Một ma trận khả nghịch, điều kiện cần và đủ là định thức ma trận đó khác 0.
Chứng minh ma trận khả nghịch
Ví dụ: Chứng minh ma trận sau khả nghịch:
\(A=\left|\begin{matrix}2 & 1 & -1 \\
0 & 1 & 3 \\
2 & 1 & 1
\end{matrix}\right|\)
Giải
Để ma trận A khả nghịch thì det(A) ≠ 0.
det(A)=2*1*1+1*3*2+(-1)*0*1-2*1*(-1)-1*3*2-1*0*1 = 4.
det(A) =4 ≠ 0. Vậy ma trận A khả nghịch.
Bài tập tìm m để ma trận khả nghịch
Bài 1: Tìm a để ma trận khả nghịch

Hướng dẫn giải
Nhân -2 hàng 1 vào hàng 3


Nhân -1/2 hàng 2 vào hàng 3
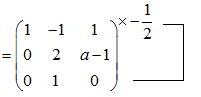

Để a khả nghịch thì det ≠ 0
=> 2.(-0.5a+ 0.5) ≠0
=> a≠1
Bài 2: Tìm m để ma trận A khả nghịch
\(A=\begin{pmatrix}m & 1\\
0 & m-1
\end{pmatrix}
\begin{pmatrix}
m-1 & 0\\
1 & m-1
\end{pmatrix}
\begin{pmatrix}
m-1 & 0\\
1 & m-2
\end{pmatrix}\)
Giải
det A ≠ 0 => \(m.(m-2)(m-1)^{4} ≠ 0\)
Vậy để A khả nghịch thì \(m\neq 0\wedge m\neq 1\wedge m\neq 2\)
Bài 3: Tìm x để ma trận khả nghịch
\(A=\begin{pmatrix}2 & 1& x\\
3 & 7& 0\\
1 & 0& 0
\end{pmatrix}\)
Giải
Đổi vị trí cột 3 và cột 1
\(A=\begin{pmatrix}x & 1& 2\\
0 & 7& 3\\
0 & 0& 1
\end{pmatrix}\)
Như vậy định thức của ma trận chính là đường chéo chính => det A = x.7.1
Để A khả nghịch thì det(A) ≠ 0 => x≠ 0
Bài 4: Tìm m ma trận 4×4 khả nghịch
\(\begin{pmatrix}2 & 1& 1& -4\\
0 & 4& 4& -2\\
0 & 0& 4& m\\
0 & 0& 4& -2
\end{pmatrix}\)
Giải
\(det(A)=2\begin{vmatrix}4 & 4& -2\\
0 & 4& m\\
0 & 4& -2
\end{vmatrix}\)
= 2.4[4.(-2)-4m]=-32(2+m)
Để ma trận khả nghịch thì det(A) ≠ 0 => m≠ -2
Cách bấm ma trận nghịch đảo
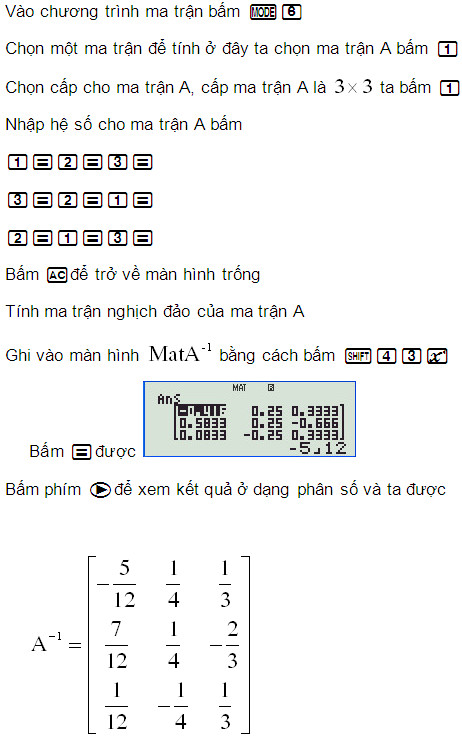
Liên quan: Top 5 App/Web giải đại số tuyến tính giúp bạn đạt điểm cao
Ứng dụng của ma trận nghịch đảo
Ma trận nghịch đảo có nhiều ứng dụng đại số tuyến tính và các lĩnh vực khác. Dưới đây là một số ví dụ về ứng dụng của ma trận nghịch đảo:
- Giải phương trình tuyến tính: Ma trận nghịch đảo cho phép chúng ta giải các hệ phương trình tuyến tính một cách hiệu quả. Bằng cách nhân vế trái và vế phải của hệ phương trình với ma trận nghịch đảo của ma trận hệ số, chúng ta có thể tìm ra nghiệm của hệ phương trình.
- Tính chất độc lập tuyến tính: Ma trận nghịch đảo liên quan mật thiết đến khái niệm độc lập tuyến tính.
Câu hỏi thường gặp
Tại sao ta cần ma trận nghịch đảo?
Bởi vì ma trận không thể chia và cũng không có khái niệm chia ma trận. Vì vậy thay vì chia ma trận, ta có thể nhân với một ma trận nghịch đảo.
Nghịch đảo của ma trận thường được sử dụng để tìm nghiệm của phương trình.
Tải file tài liệu ma trận nghịch đảo PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Hi vọng qua bài viết trên đây các bạn đã nắm vững kiến thức cơ bản và các dạng bài tập tìm ma trận nghịch đảo. Nếu có bất kì thắc mắc hoặc sai sót nào thì đừng ngần ngại liên hệ với mình nhé. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net
Bài viết liên quan: