Gửi tới bạn đọc kiến thức cơ bản cùng các dạng bài tập về tìm cơ sở và số chiều của không gian vecto trong môn toán cao cấp môn đại số và hình học giải tích giúp các bạn ôn tập dễ dàng.
Xem thêm:
- tìm giá trị riêng của ma trận
- chéo hoá ma trận
- bài tập và cách tìm ma trận chuyển cơ sở
I. Cơ sở của không gian vecto
Định nghĩa
Một hệ sinh độc lập tuyến tính của một không gian vectơ khác vectơ 0 được gọi là cơ sở của nó.
Chú ý: Không gian vectơ 0 không có cơ sở hay số vectơ trong cơ sở của không gian vectơ không bằng 0.
S={e1 + e2 ,…,en } là cơ sở của không gian V nếu:
- S độc lập tuyến tính
- ∀ phần tử x đều được biểu diễn qua S: x= k1e1+k2e2+…+knen
Cơ sở chính tắc của r2
- \(R^{2}\)={a,b}
- (a,b,c)=a(1,0)+b(0,1)S={(1,0),(0,1)
- dim \(R^{n}=n\)
- có 2 vecto
Cơ sở chính tắc của r3
- \(R^{3}\)={a,b,c}
- (a,b,c)=a(1,0,0)+b(0,1,0)+c(0,0,1)
- S={(1,0,0),(0,1,0),(0,0,1)}
- dim \(R^{n}=n\)
- có 3 vecto
Cơ sở chính tắc của không gian \(M_{2}\)
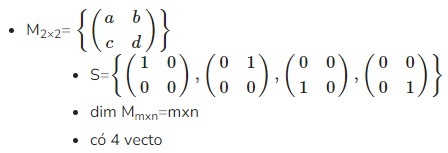
Liên quan:
Cơ sở chính tắc của \(P_{2}\)
- P2={a+bx+cx2}
- S={1,x,x2}
- dim \(P_{n}=n+1\)
- có 3 vecto.
Chứng minh 1 hệ là cơ sở
S là cơ nếu nếu thoả mãn 2 điều kiện:
- S độc lập tuyến tính.
- dim V= số phần tử S.
II. Số chiều của không gian vecto
Định nghĩa
Số vectơ trong một cơ sở K không gian vectơ V được gọi là số chiều của V.
Kí hiệu: \(dim_{K}V\). Nếu không cần chỉ rõ trường K cụ thể, ta có thể viết đơn giản \(dimV\).
III. Cách tìm dim của ma trận
Số chiều không gian V=dimV=n= số phần tử.
- dim của không gian r2,r3: \(R^{n}=n\).
- dim của không gian \(P_{n}\): \(P_{n}=n+1\).
- dim của không gian \(M_{mxn}=m.n\)
IV. Tìm tọa độ của vecto trong cơ sở

Lưu ý:
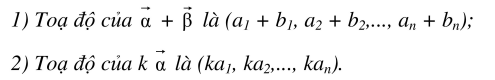
Xem thêm: ánh xạ tuyến tính
Bài tập tìm cơ sở không gian vectơ
Hệ vecto nào là cơ sở của r2


>>>Liên quan: định thức ma trận
Chứng minh cơ sở của r3
Bài 1: Kiểm tra S có phải là cơ sở của không gian vecto V không
a. S={(1,0,0),(0,1,0),(0,0,1)}⊂R4
S có 3 phần tử mà dim R4 =4 => S không phải là cơ sở
Bài 2: Chứng minh s là một cơ sở của r3
b. S={(1,2,3),(4,5,6),(7,8,9)}⊂R3
số phần tử =dim R3 =3
Xét định thức:
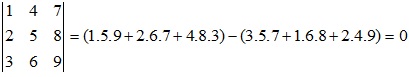
> phụ thuộc tuyến tính
=> S không là sơ sở
c.S={1+x,2-x+3x2,3x-x2}⊂P2
Số phần tử=dim P2 =3
Xét định thức:

=> độc lập tuyến tính
=> S là cơ sở
Hệ vecto nào là cơ sở của r3
a. u1(1,2), u2(3,4), u3(5,6) đối với R2
-Không vì cơ sở R2 có 2 vecto
b. u1(1,2,3), u2(3,4,5), u3(4,5,6) đối với R3
-Có vì cơ sở R3 có 3 vecto
c. u1(2,1), u2(3,0) đối với R2
Số phần tử dim R2 =2
Xét ma trận bổ sung
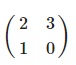
det=-3≠0 => độc lập tuyến tính => là sơ sở

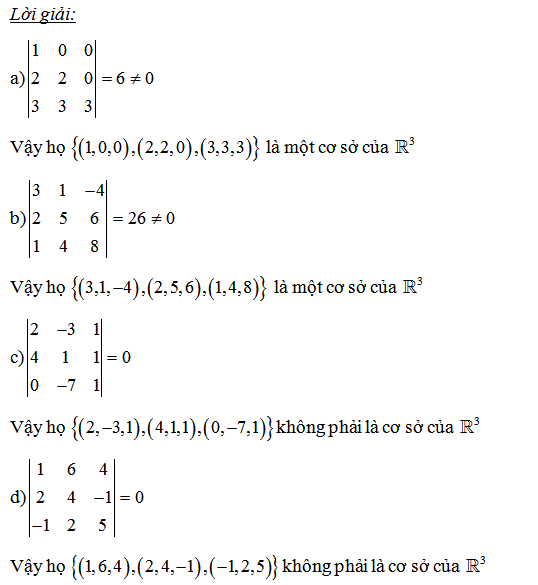
Hệ vecto nào là cơ sở của P2



Hệ vecto nào là cơ sở của M2



>>>Xem thêm: nghiệm tầm thường và nghiệm không tầm thường
Tìm cơ sở và số chiều của không gian nghiệm




Xác định số chiều và một cơ sở của không gian nghiệm các hệ sau




Bài tập tìm tọa độ của vecto trong cơ sở
Tìm ma trận toạ độ và vecto toạ độ của w trong cơ sở S



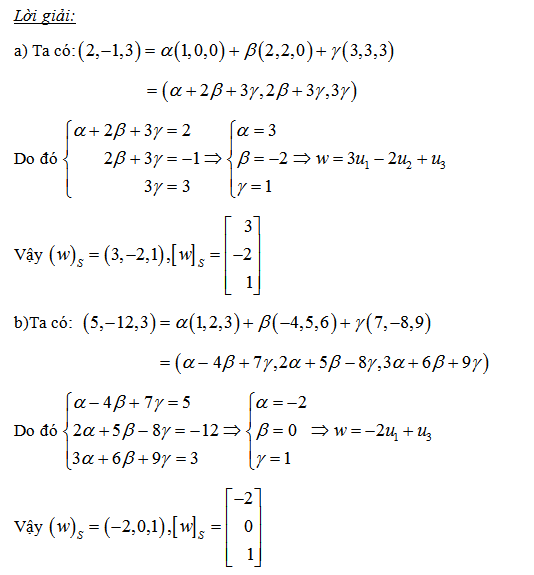
Tìm toạ độ của ma trận trong cơ sở

Tìm toạ độ của vecto trong cơ sở


Tìm toạ độ của vecto theo cơ sở

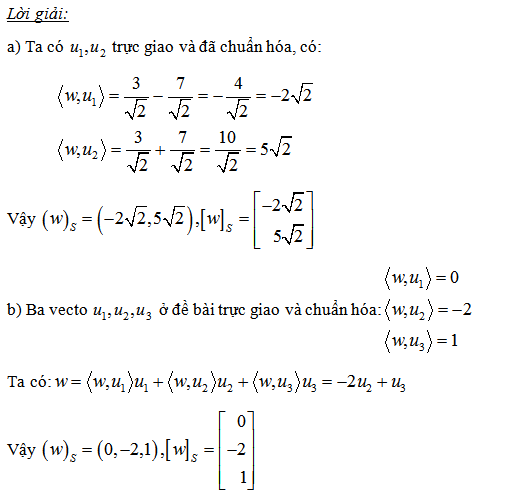
Ok xong, trên đây là một số kiến thức cơ bản cùng hướng dẫn cách giải các bài toàn về tìm số chiều, cơ sở, toạ độ của vecto. Nếu có bất kì thắc mắc nào thì đừng ngần ngại liên hệ với mình nhé. Cảm ơn các bạn đã tham khảo tài liệu cơ sở không gian vecto trên ttnguyen.net
Tải file tài liệu Cơ sở không gian vecto giáo trình, lý thuyết, bài tập PDF
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Bài viết liên quan: