Giả sử bạn muốn biết xác suất nhận được số 1 trên cuộn xúc xắc. Nếu bạn tung một con xúc xắc 20 lần, xác suất ném được số 1 là 1/6. Ném xúc xắc 20 lần và bạn có phân phối nhị thức là (n = 20, p = 1/6). Vậy làm thế nào để tính công thức trên? Sau đây hãy cùng ttnguyen.net tìm hiểu qua bài viết phân phối nhị thức dưới đây nhé!
Xem thêm:
phân phối Poisson là gì? Công thức, quy luật và bài tập
phân phối xác suất thành phần – Các đặc trưng và bài tập
giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Phân phối nhị thức là gì?
Phân phối nhị thức là một phân phối xác suất trong lý thuyết xác suất thống kê, mô tả xác suất của số lần thành công trong các thí nghiệm độc lập và rời rạc trong một số cố định nghiên cứu.
Phân phối được gọi là “nhị thức” vì chỉ xảy ra trong hai trường hợp (thành công hoặc thất bại). Phân phối nhị thức có hai tham số chính:
- p: xác suất thành công trong mỗi thí nghiệm
- n: số lần thí nghiệm được thực hiện
Ký hiệu: \(X ∼ B(n,p)\)
Ví dụ minh hoạ: Tung một đồng xu 10 lần, xác suất xuất hiện mặt ngửa là 0,5. Số lần mặt ngửa xuất hiện trong 10 lần tung chính là một phân phối nhị thức.
2. Công thức phân phối nhị thức
Công thức phân phối nhị thức dành cho bất kỳ biến ngẫu nhiên X, được cho bởi:
\(P(X=k)=C^{k}_{n}p^{k}(1-p)^{n-k}\)
Trong đó:
- n: số lần phép thử
- k=0,1,2,…,n
- p: xác suất thành công của phép thử
Trung bình và phương sai phân phối nhị thức:
Đối với phân phối nhị thức, giá trị trung bình, phương sai và độ lệch chuẩn của số lần thành công nhất định được biểu diễn bằng cách sử dụng các công thức
- Trung bình: \(E(X) = n.p\)
- Phương sai: \(V(X) = n.p.q\)
- Độ lệch chuẩn: \(σ = √(n.p.q)\)
Trong đó: p là xác suất thành công; q là xác xuất thất bại được tính bởi q = 1-p.
Xem thêm:
- phân phối mũ – Công thức tính và bài tập có lời giải
- phân phối siêu bội – Công thức và bài tập có lời giải
- bảng phân phối chi bình phương, Gamma | Cách tra và bài tập
3. Bảng phân bố nhị thức
Bảng phân bố nhị thức thường được sử dụng để liệt kê các giá trị xác suất tương ứng với các giá trị k (số lần thành công).

Ví dụ, với n=5 và p=0.5, bảng phân bố sẽ như sau:
| X (số lần thành công) | 0 | 1 | 2 | 3 | 4 | 5 |
| P(X=k) | 0.031 | 0.156 | 0.313 | 0.313 | 0.156 | 0.031 |
4. Tính chất của quy luật phân phối nhị thức
Các tính chất của phân phối nhị thức là:
- Có hai kết quả có thể xảy ra: đúng hoặc sai, thành công hoặc thất bại, có hoặc không.
- Có n số phép thử độc lập hoặc một số cố định n lần thử nghiệm lặp lại.
- Xác suất thành công hay thất bại vẫn như nhau cho mỗi lần thử.
- Chỉ tính số lần thành công trong số n lần thử nghiệm độc lập.
- Mỗi phép thử là một phép thử độc lập, có nghĩa là kết quả của một phép thư không ảnh hưởng đến kết quả của phép thử khác.
5. Bài tập phân phối nhị thức có lời giải
Bài 1: Tỷ lệ mắc bệnh ở 1 địa phương là p = 1%. Người ta lấy máu từng người để thử nghiệm theo cách 2:
– Cách 1: Mỗi người lấy máu làm một việc thử nghiệm.
– Cách 2: Lấy máu 10 người cùng làm 1 lần thử nghiệm, nếu trong mẫu âm tính chung thì thôi, nếu phát âm tính chung mẫu thì làm lại từng người, mỗi người 1 thử nghiệm riêng.
Với 1000 người cần kiểm tra, do đó, so sánh hai cách xem cách nào có lợi hơn (nghĩa là số kiểm tra phải ít hơn).
Giải

| X | 1 | 10 |
| P | 0,0956 |
Như vậy số kiểm tra trung bình là: E (X) = 9,6 => số kiểm tra là 960.
Xem thêm:
- Phân phối xác suất có điều kiện và kỳ vọng có điều kiện
- Phân phối xác suất đồng thời – Cách lập bảng có đáp án
Bài 2: Tỷ lệ người dân tham gia trên mạng lưới giao dịch có sự hiểu biết về luật giao dịch là 90%. Tại một nút giao diện có 5 người giao diện trong phạm vi luật. Gọi X là một số người am hiểu luật nhưng cố gắng tình luật trong 5 người đó.
a) Lập bảng phân phối xác suất của X.
b) Tính E (3- 5X) và V (3X-2).
c) Nếu có 30 người trong phạm vi luật, thì trung bình có bao nhiêu người hiểu biết luật nhưng cố gắng trong phạm vi? Có bao nhiêu người trong phạm vi luật làm người không hiểu luật?
Giải
Bài toán được thử nghiệm dãy phép thử Bernoulli n = 5; p = 0,9; q = 0,1
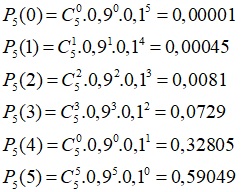
a. Bảng phân phối là:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0,00001 | 0,00045 | 0,0081 | 0,0729 | 0,32805 | 0,59049 |
b. X có dạng phân phối nhị thức với n = 5; p = 0,9 => E (X) = 5,0,9 = 4,5
E (3-5X) = 3-5E (X) = 3-5.4,5 = -19,5
V (3X-2) = 9V (X) = 9.0,1,5 = 4,5
c. Gọi Y là một số luật trong một dãy
Y có phân phối nhị thức với n = 30; p = 0,9
Y là biến ngẫu nhiên rời rạc : Y = 0,1, …, 30
Trung bình người hiểu luật nhưng cố tình phạm vi: E (Y) = np = 30.0,9 = 27
Gọi k là một số của dãy luật mà người ta chưa biết Luật
![]()
Bài 13: Một báo cáo đã cung cấp các dữ liệu về 10 phần mềm phá hoại đầu bảng tính tới năm 2002. Đứng đầu nhóm này là loại vi rút mạng có tên “Klez” và tới năm 2002 nó vẫn là loại vi rút có sức phá hoại lớn nhất. Có 61,22% phiên bản loại vi rút này. Giả sử có 20 phiên bản phần mềm phá hoại và các bản gốc của các phiên bản phần mềm này là độc lập
a) Xác suất để có ít nhất một phiên bản “Klez” là bao nhiêu?
b) Trung bình và độ lệch chuẩn của số phiên bản “Klez” trong 20 phiên bản phần mềm phá hoại là bao nhiêu?
c) Xác suất có 3 hay nhiều hơn 3 phiên bản “Klez” là bao nhiêu?
Giải

6. Các câu hỏi thường gặp về phân phối nhị thức
Phân phối nhị thức và ứng dụng thực tế
Như chúng ta đã biết, phân phối nhị thức cung cấp khả năng có một tập hợp các kết quả khác nhau. Trong cuộc sống thực, khái niệm này được sử dụng cho:
- Nếu một loại thuốc mới được giới thiệu để chữa bệnh, thì thuốc đó sẽ chữa khỏi bệnh (thành công) hoặc không chữa khỏi bệnh (thất bại).
- Nếu bạn mua một vé số, bạn sẽ trúng tiền hoặc không. Về cơ bản, bất cứ điều gì bạn có thể nghĩ đến chỉ có thể là thành công hoặc thất bại đều có thể được biểu diễn bằng phân phối nhị thức.
- Tìm số lượng nguyên liệu thô và đã sử dụng trong khi sản xuất một sản phẩm.
- Thực hiện một cuộc khảo sát đánh giá tích cực và tiêu cực từ công chúng cho bất kỳ sản phẩm hoặc địa điểm cụ thể nào.
- Tìm số lượng nhân viên nam và nữ trong một tổ chức.
- Số phiếu thu được của một ứng cử viên trong một cuộc bầu cử được tính dựa trên 0 hoặc 1 xác suất
Phân phối nhị thức và phân phối chuẩn
Sự khác biệt chính giữa phân phối nhị thức và phân phối chuẩn là phân phối nhị thức là rời rạc, trong khi phân phối chuẩn là liên tục. Nó có nghĩa là phân phối nhị thức có số lượng sự kiện hữu hạn, trong khi phân phối chuẩn có vô số sự kiện. Trong trường hợp, nếu cỡ mẫu cho phân phối nhị thức là rất lớn, thì đường cong phân phối cho phân phối nhị thức tương tự như đường cong phân phối chuẩn.
Tại sao phân phối nhị thức lại quan trọng?
Phân phối nhị thức được sử dụng để tính khả năng đạt hoặc kết quả không đạt trong một cuộc khảo sát hoặc thử nghiệm được lặp lại nhiều lần. Chỉ có hai kết quả tiềm năng cho kiểu phân phối này. Nói rộng hơn, phân phối là một phần quan trọng của việc phân tích các tập dữ liệu để ước tính tất cả các kết quả tiềm năng của dữ liệu và tần suất chúng xảy ra. Dự báo và hiểu được sự thành công hay thất bại của các kết quả là điều cần thiết để phát triển doanh nghiệp.
Ý nghĩa của phân phối nhị thức là gì?
Phân phối nhị thức chỉ cho hai kết quả trong một thử nghiệm: thành công hoặc thất bại.
Tài liệu phân phối nhị thức PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Trên đây là một số kiến thức về phân phối nhị thức. Hy vọng bài viết hữu ích với bạn.
Bài viết cùng chủ đề:
phân phối Fisher – snedecor | Cách tra bảng đầy đủ PDF
bảng phân phối student | Cách tra bảng giá trị đầy đủ PDF
phân phối đều là gì? Công thức và bài tập có lời giải