Thống kê là một nhánh của toán học liên quan đến các con số và phân tích dữ liệu. Thống kê là nghiên cứu về việc thu thập, phân tích, giải thích, trình bày và tổ chức dữ liệu. Lý thuyết thống kê định nghĩa thống kê là một hàm của mẫu trong đó bản thân hàm độc lập với phân phối của mẫu.
Sau đây là bài viết tổng hợp công thức thống kê trong môn xác xuất thống kê giúp các bạn ôn tập được dễ dàng hơn!
Bài viết liên quan: Công thức tính xác suất chi tiết đầy đủ nhất – xem phát hiểu luôn
Bảng công thức thống kê
Các công thức thống kê quan trọng được liệt kê trong biểu đồ dưới đây:
1. Thống kê
Để dễ xử lý ta viết số liệu của mẫu cụ thể dưới dạng tần số như sau:
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
| Các giá trị đặc trưng | Mẫu cụ thể |
| Giá trị trung bình | \(\bar{x}=\frac{x_{1}.n_{1}+…+x_{k}.n_{k}}{n}\) |
| Phương sai không hiệu chỉnh | \({S_{x}}^{2}=\frac{(x_{1}-{\bar{x}})^{2}.{n_{1}}+…+(x_{k}-{\bar{x}})^{2}.{n_{k}}}{n}\) |
| Phương sai có hiệu chỉnh | \({S_{x}}^{2}=\frac{(x_{1}-{\bar{x}})^{2}.{n_{1}}+…+(x_{k}-{\bar{x}})^{2}.{n_{k}}}{n-1}\) |
Ví dụ: Một máy tự động đóng bột vào bao. Cân ngẫu nhiên 15 bao được bảng phân phối tần số thực nghiệm sau:

Giải
Giá trị trung bình mẫu:
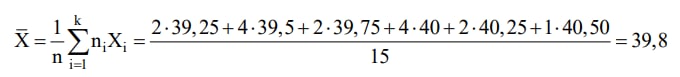
Phương sai có hiệu chỉnh
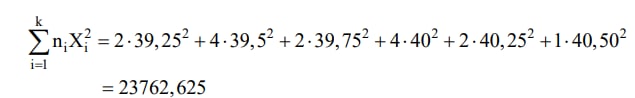
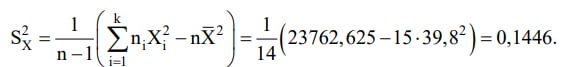
Xem thêm: Bài tập biến ngẫu nhiên liên tục có đáp án & lời giải chi tiết
2. Ước lượng khoảng
Khoảng tin cậy cho giá trị trung bình
Trường hợp: \(\sigma \) đã biết, n<30
| Các giá trị đặc trưng | Công thức |
| Ước lượng đối xứng | \(\varphi(z_{\frac{\alpha }{2}})=\frac{1-a}{2}\rightarrow z_{\frac{\alpha }{2}}\Rightarrow \varepsilon =z_{\frac{\alpha }{2}}.\frac{\sigma }{\sqrt{n}}\Rightarrow (\bar{x}-\varepsilon ;\bar{x}+\varepsilon)\) |
| Ước lượng chênh lệch trái | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sigma }{\sqrt{n}}\Rightarrow (-\infty ;\bar{x}+\varepsilon)\) |
| Ước lượng chênh lệch phải | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sigma }{\sqrt{n}}\Rightarrow (\bar{x}-\varepsilon ;+\infty )\) |
Ví dụ: Trọng lượng một loại sản phẩm là biến ngẫu nhiên phân phối chuẩn với độ
lệch chuẩn là 1 gam. Cân thử 25 sản phẩm loại này ta thu được kết quả sau:

Với độ tin cậy 95%, hãy tìm khoảng tin cậy đối xứng của trọng lượng trung bình
của loại sản phẩm nói trên.
Giải

Trường hợp: \(\sigma \) chưa biết, n<30
| Các giá trị đặc trưng | Công thức |
| Ước lượng đối xứng | \(1-\alpha\rightarrow \frac{\alpha }{2}\rightarrow t_{(n-1;\frac{\alpha }{2})}\Rightarrow \varepsilon =t_{(n-1;\frac{\alpha }{2})}.\frac{s}{\sqrt{n}}\Rightarrow (\bar{x}-\varepsilon ;\bar{x}+\varepsilon )\) |
| Ước lượng chênh lệch trái | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sigma }{\sqrt{n}}\Rightarrow (-\infty ;\bar{x}+\varepsilon)\) |
| Ước lượng chênh lệch phải | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sigma }{\sqrt{n}}\Rightarrow (\bar{x}-\varepsilon ;+\infty )\) |
Ví dụ: Năng suất một loại cây trồng là biến ngẫu nhiên có phân phối chuẩn. Thu
hoạch tại một số điểm được kết quả sau:

Với độ tin cậy 95%, hãy ước lượng năng suất trung bình bằng khoảng tin cậy đối xứng.
Giải

Khoảng tin cậy cho tỉ lệ
| Các giá trị đặc trưng | Công thức |
| Ước lượng đối xứng | \(\varphi(z_{\frac{\alpha }{2}})=\frac{1-a}{2}\rightarrow z_{\frac{\alpha }{2}}\Rightarrow \varepsilon =z_{\frac{\alpha }{2}}.\frac{\sqrt{f(1-f)}}{\sqrt{n}}\Rightarrow (f-\varepsilon ;f+\varepsilon)\) |
| Ước lượng chênh lệch trái | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sqrt{f(1-f)}}{\sqrt{n}}\Rightarrow (0;f+\varepsilon)\) |
| Ước lượng chênh lệch phải | \(\varphi(z_{a})=0,5-\alpha\rightarrow z_{a}\Rightarrow \varepsilon =z_{a}.\frac{\sqrt{f(1-f)}}{\sqrt{n}}\Rightarrow (f-\varepsilon;1)\) |
Ví dụ: Để ước lượng tỷ lệ bệnh sốt rét ở Đồng Bằng Sông Cửu Long.
1) Nếu muốn sai số ước lượng không quá 2% ở độ tin cậy 95% thì cần quan sát ít nhất bao nhiêu người ?
2) Ta quan sát ngẫu nhiên 200 người, thấy có 24 người mắc bệnh sốt rét.
a) Tìm khoảng ước lượng đối xứng của p với độ tin cậy 95%,
b) Tìm khoảng ước lượng tối đa, tối thiểu của p với độ tin cậy 95%.
c) Nếu muốn sai số ước lượng không quá 2% ở độ tin cậy 95% thì cần quan sát ít nhất mấy người ?
Giải


Xem thêm: Bài tập về phân phối Poisson có lời giải | Xem 2 phút hiểu luôn
Khoảng tin cậy cho phương sai
| Các giá trị đặc trưng | Công thức |
| Ước lượng đối xứng | \(1-\alpha\rightarrow \frac{\alpha }{2}\rightarrow \chi_{2} ={\chi^{2}_{(n-1;\frac{\alpha }{2})}}\) \(1-\alpha\rightarrow 1-\frac{\alpha }{2}\rightarrow \chi_{1} ={\chi^{2}_{(n-1;\frac{\alpha }{2})}}\) \(\Rightarrow (\frac{(n-1).s^{2}}{\chi_{2}};\frac{(n-1).s^{2}}{\chi_{1}})\) |
| Ước lượng chênh lệch trái | \(1-\alpha\rightarrow \chi_{1} ={\chi^{2}_{(n-1;1-\alpha)}} \Rightarrow (0;\frac{(n-1).s^{2}}{\chi_{1}})\) |
| Ước lượng chênh lệch phải | \(1-\alpha\rightarrow \chi_{1} ={\chi^{2}_{(n-1;\alpha)}} \Rightarrow (\frac{(n-1).s^{2}}{\chi_{2}};+\infty )\) |
Ví dụ: Khảo sát chỉ tiêu X của một loại sản phẩm, người ta quan sát một mẫu và có
kết quả sau



Trường hợp 2: Tính \((n-1).s^{2}=\sum_{i=1}^{k}.ni(x-\mu )^{2}\)
| Các giá trị đặc trưng | Công thức |
| Ước lượng đối xứng | \(1-\alpha\rightarrow \frac{\alpha }{2}\rightarrow \chi_{2} ={\chi^{2}_{(n;\frac{\alpha }{2})}}\) \(1-\alpha\rightarrow 1-\frac{\alpha }{2}\rightarrow \chi_{1} ={\chi^{2}_{(n;1-\frac{\alpha }{2})}}\) \(\Rightarrow (\frac{(n-1).s^{2}}{\chi_{2}};\frac{(n-1).s^{2}}{\chi_{1}})\) |
| Ước lượng chênh lệch trái | \(1-\alpha\rightarrow \chi_{1} ={\chi^{2}_{(n;1-\alpha)}} \Rightarrow (0;\frac{(n-1).s^{2}}{\chi_{1}})\) |
| Ước lượng chênh lệch phải | \(1-\alpha\rightarrow \chi_{1} ={\chi^{2}_{(n;\alpha)}} \Rightarrow (\frac{(n-1).s^{2}}{\chi_{2}};+\infty )\) |
Lời kết
Tóm lại, Thống kê gắn liền với việc thu thập, phân loại, sắp xếp và trình bày dữ liệu số. Nó cho phép chúng tôi giải thích các kết quả khác nhau từ nó và dự báo nhiều khả năng. Thống kê đề cập đến các dữ kiện, quan sát và thông tin chỉ ở dạng dữ liệu số. Với sự trợ giúp của số liệu thống kê, chúng ta có thể tìm thấy nhiều thước đo khác nhau về khuynh hướng trung tâm và độ lệch của các giá trị khác nhau so với trung tâm.
Cảm ơn các bạn đã tham khảo bài viết tổng hợp công thức thống kê. Chúc các bạn học tập tốt