Ước lượng khoảng tin cậy là một công cụ quan trọng trong thống kê, giúp xác định mức độ chắc chắn của các thông tin thu thập được. Trong bài viết này, chúng ta sẽ tìm hiểu về cách giải bài tập ước lượng khoảng tin cậy trung bình cho một số tham số thống kê quan trọng, bao gồm trung bình, phương sai, và tỷ lệ tổng thể.
Xem thêm:
ước lượng điểm – Cách tìm và bài tập có lời giải
I. Công thức ước lượng khoảng tin cậy
1. Ước lượng khoảng tin cậy cho trung bình khi biết phương sai tổng thể
\(\overline{X} – \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} < \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}}\)2. Ước lượng khoảng tin cậy cho trung bình khi chưa biết phương sai tổng thể
\(\overline{X} – \frac{S}{\sqrt{n}}t^{n-1}_{\frac{\alpha}{2}} < \mu < \overline{X} + \frac{S}{\sqrt{n}}t^{n-1}_{\frac{\alpha}{2}}\)3. Ước lượng khoảng tin cậy cho phương sai tổng thể
\(\frac{(n-1)S^2}{\chi^2_\frac{\alpha}{2}} < \sigma^2 < \frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}}\)4. Ước lượng khoảng tin cậy cho tỉ lệ tổng thể
\(f-\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}} < p < f+\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}}\)5. Tổng hợp công thức ước lượng khoảng tin cậy đầy đủ nhất
| Ước lượng | Khoảng 2 phía | Khoảng bên phải | Khoảng bên trái | |
| \(\mu \) | Biết \(\sigma^2\) | \(\overline{X} – \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} < \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}}\) | \(\overline{X} – \frac{\sigma}{\sqrt{n}}z_{\alpha} < \mu\) | \(\mu < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\alpha}\) |
| Chưa biết \(\sigma^2\) | \(\overline{X} – \frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}^{n-1} < \mu < \overline{X} + \frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}^{n-1}\) | \(\overline{X} – \frac{S}{\sqrt{n}}t_{\alpha}^{n-1} < \mu\) | \(\mu < \overline{X} + \frac{S}{\sqrt{n}}t_{\alpha}^{n-1}\) | |
| \(\sigma^2 \) | Biết \(\mu\) | \(\frac{nS^{*2}}{\chi_{\frac{\alpha}{2}}^{2(n-1)}} < \sigma^2 < \frac{nS^{*2}}{\chi_{1-\frac{\alpha}{2}}^{2(n-1)}}\) | \(\frac{nS^{*2}}{\chi_{\alpha}^{2(n)}} < \sigma^2\) | \(0 < \sigma^2 < \frac{nS^{*2}}{\chi_{1-\alpha}^{2(n)}}\) |
| Chưa biết \(\mu\) | \(\frac{(n-1)S^{2}}{\chi_{\frac{\alpha}{2}}^{2(n-1)}} < \sigma^2 < \frac{(n-1)S^{2}}{\chi_{1-\frac{\alpha}{2}}^{2(n-1)}}\) | \(\frac{(n-1)S^{2}}{\chi_{\alpha}^{2(n-1)}} < \sigma^2\) | \(0 < \sigma^2 < \frac{(n-1)S^{2}}{\chi_{1-\alpha}^{2(n-1)}}\) | |
| \(p \) | \(f-\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}} < p < f+\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}}\) | \(f-\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\alpha} < p\) | \(p < f+\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\alpha}\) | |
II. Giải bài tập ước lượng khoảng tin cậy có lời giải
1. Bài tập ước lượng khoảng tin cậy cho muy
| Khoảng tin cậy hai phía(đối xứng) | Khoảng bên phải | Khoảng bên trái |
| \(\overline{X} – \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} < \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}}\) | \(\overline{X} – \frac{\sigma}{\sqrt{n}}z_{\alpha} < \mu < + \infty \) | \(– \infty< \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}z_{\alpha}\) |
Ví dụ 1: Chiều dài một loại súng nước là biến ngẫu nhiên phân bố chuẩn với độ lệch chuẩn là 3cm. Một người nghiên cứu loại súng này muốn ước tính chiều dài trung bình của các khẩu súng. Bằng cách đo ngẫu nhiên 25 súng khác nhau, thu được chiều dài trung bình là 13,5cm.
a) Với độ tin cậy 95%, chiều dài trung bình của súng nằm trong khoảng nào? X: chiều dài (cm) của súng.
b) Nếu muốn độ chính xác ở ý a) tăng gấp đôi và giữ nguyên độ tin cậy thì cần đo thêm bao nhiêu chiếc súng?
c) Nếu không điều tra thêm và muốn giảm độ dài khoảng tin cậy xuống còn 2/3 so với lúc trước, độ tin cậy lúc này là bao nhiêu?
Giải
a.

b.

c.

Bài 2: Đường kính của một loại bưởi là biến ngẫu nhiên có phương sai 9cm2. Đo ngẫu nhiên 50 trái thấy đường kính trung bình đạt 20cm. Với độ tin cậy 95%, đường kính trung bình của loại bưởi này tối thiểu bao nhiêu?
Giải

2. Bài tập ước lượng khoảng tin cậy cho trung bình
| Khoảng tin cậy hai phía(đối xứng) | Khoảng bên phải | Khoảng bên trái |
| \(\overline{X} – \frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}^{n-1} < \mu < \overline{X} + \frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}^{n-1}\) | \(\overline{X} – \frac{S}{\sqrt{n}}t_{\alpha}^{n-1} < \mu\) | \(\mu < \overline{X} + \frac{S}{\sqrt{n}}t_{\alpha}^{n-1}\) |
Ví dụ 1: Cân 40 bao vật liệu xây dựng thấy trung bình mẫu bằng 50kg và độ lệch chuẩn mẫu bằng 0,4kg. Biết rằng trọng lượng bao vật liệu là biến ngẫu nhiên phân phối chuẩn.
a. Với độ tin cậy 95%, ước lượng trọng lượng trung bình của bao vật liệu.
b. Nếu muốn độ chính xác tăng gấp đôi mà vẫn giữ nguyên độ tin cậy thì cần điều tra thêm bao nhiêu bao?
c. Với độ tin cậy 90%, ước lượng tối thiểu trọng lượng trung bình của bao vật liệu.
Giải
a.
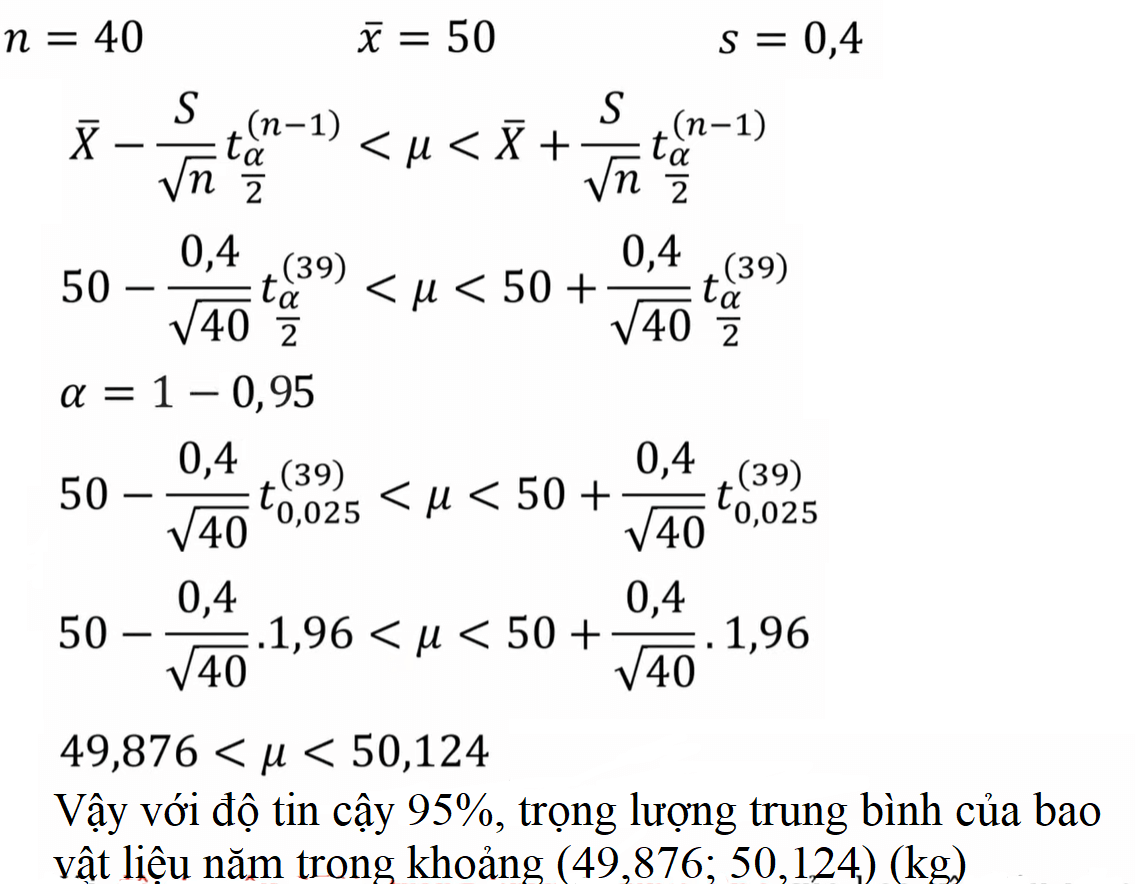
b.

c.

3. Bài tập ước lượng khoảng tin cậy cho phương sai tổng thể
| Khoảng tin cậy hai phía(đối xứng) | Khoảng bên phải | Khoảng bên trái |
| \(\frac{(n-1)S^{2}}{\chi_{\frac{\alpha}{2}}^{2(n-1)}} < \sigma^2 < \frac{(n-1)S^{2}}{\chi_{1-\frac{\alpha}{2}}^{2(n-1)}}\) | \(\frac{(n-1)S^{2}}{\chi_{\alpha}^{2(n-1)}} < \sigma^2\) | \(0 < \sigma^2 < \frac{(n-1)S^{2}}{\chi_{1-\alpha}^{2(n-1)}}\) |
Ví dụ 2: Cân 40 bao vật liệu xây dựng thấy trung bình mẫu bằng 50kg và độ lệch chuẩn mẫu bằng 0,4kg. Biết rằng trọng lượng bao vật liệu là biến ngẫu nhiên phân phối chuẩn. Ước lượng độ phân tán tối đa về trọng lượng của bao vật liệu với độ tin cậy 99%.
Giải

4. Bài tập ước lượng khoảng tin cậy cho tỉ lệ tổng thể
| Khoảng tin cậy hai phía(đối xứng) | Khoảng bên phải | Khoảng bên trái |
| \(f-\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}} < p < f+\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\frac{\alpha}{2}}\) | \(f-\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\alpha} < p\) | \(p < f+\frac{\sqrt{f(1-f)}}{\sqrt{n}}z_{\alpha}\) |
Ví dụ 1: Điều tra ngẫu nhiên 200 trẻ e ở một khu vực thấy có 146 trẻ đã tiêm phòng tại trạm y tế của khu vực.
a. Với độ tin cậy 90%, ước lượng tỉ lệ trẻ được tiêm phòng tại trạm y tế của khu vực.
b. Với độ tin cậy 90%, ước lượng số trẻ em trong khu vực này, biết trạm y tế đã tiêm phòng cho 10000 cháu.
c. Nếu vẫn sử dụng mẫu số liệu đang có và muốn độ dài khoảng tin cậy giảm còn 1 nửa thì cần sử dụng độ tin cậy bằng bao nhiêu?
Giải
a.

b.

c.

Hy vọng rằng thông qua bài viết này, bạn đã nắm được cách làm bài tập ước tính khoảng tin cậy trung bình cho các tham số thống kê quan trọng như trung bình, phương sai, và tỷ lệ tổng thể môn xác suất thống kê. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.
Bài viết cùng chủ đề:
bài tập biến ngẫu nhiên 2 chiều rời rạc có lời giải
kiểm định giả thuyết về phương sai