Phân bố xác suất thành phần là một bảng thể hiện xác suất của từng thành phần trong một tập hợp. Trong bài viết này TTnguyen sẽ cùng bạn tìm hiểu cách lập bảng phân phối xác suất thành phần, các đặc trưng và một số bài tập ví dụ.
Xem thêm:
- phân phối nhị thức là gì: Công thức và bài tập có lời giải
- phân phối poisson là gì? Công thức, quy luật và bài tập
- giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Phân phối xác suất thành phần là gì?
Phân phối xác suất thành phần là bảng liệt kê xác suất của một biến ngẫu nhiên đơn lẻ trong hệ thống hai biến ngẫu nhiên rời rạc. Từ bảng phân phối xác suất đồng thời, chúng ta có thể tính phân phối xác suất thành phần của từng biến như sau:
Bảng phân phối xác suất thành phần của X:
\(p(x_i)=\sum_{j=1}^{s}p_{ij}, i = 1,2,…,r\)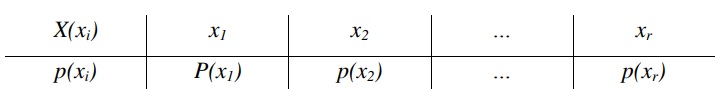
Bảng phân phối xác suất thành phần của Y:
\(p(y_i)=\sum_{i=1}^{r}p_{ij}, j = 1,2,…,s\)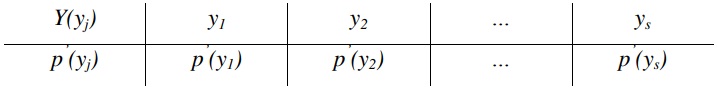
Nếu X và Y độc lập thì:
\(p_{ij}=P(X=x_i;Y=y_i)=p(x_i)p'(y_i), (i = 1,2,…,r;j = 1,2,…,s)\)2. Các đặc trưng của biến ngẫu nhiên thành phần
Kỳ vọng:
\(E(X) = \sum_{i=1}^{r} x_i p(x_i) = \sum_{i=1}^{r} \sum_{j=1}^{s} x_i p_{ij}\\E(Y) = \sum_{j=1}^{s} y_j p'(y_j) = \sum_{j=1}^{sr}\sum_{i=1}^{r} y_ji p_{ij}\)
Phương sai:
\(V(X) = \sum_{i=1}^{r} x^2_i p(x_i) – [E(X)]^2 = \sum_{i=1 }^{r}\sum _{j=1 }^{s }x^2_ip_{ij} – [E(X)]^2\\V(Y)=\sum _{j= 1 } ^{ s }y^2_jp'(y_j)-[E(Y)]^2=\sum _{ j= 1 } ^{ s }\sum _{ i= 1 } ^{ r }y^2_j p_{ij}-[E( Y )]^ 2\)
Độ lệch chuẩn:
\(\sigma(X) = \sqrt{V(X)} \\\sigma(Y) = \sqrt{V(Y)}\)
3. Bài tập phối xác suất thành phần có lời giải
Bài 1: Cho biến ngẫu nhiên 2 chiều với bảng phân phối xác suất đồng thời được cho như sau:
Hãy lập bảng phân bố xác suất thành phần của X và Y
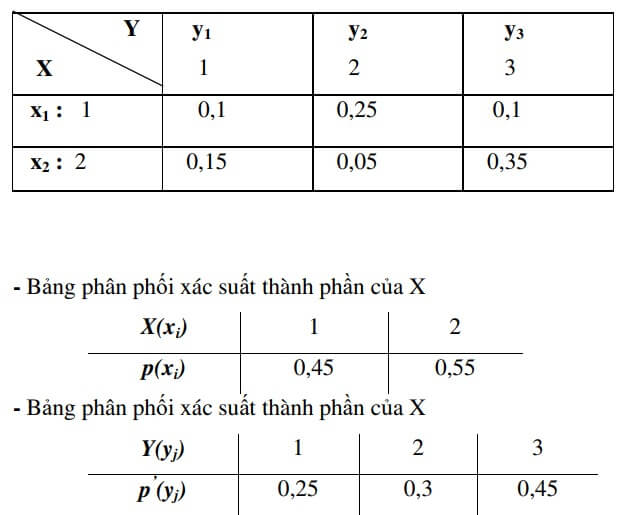
Tính các số đặc trưng của các biến ngẫu nhiên thành phần X và Y. Ta có:
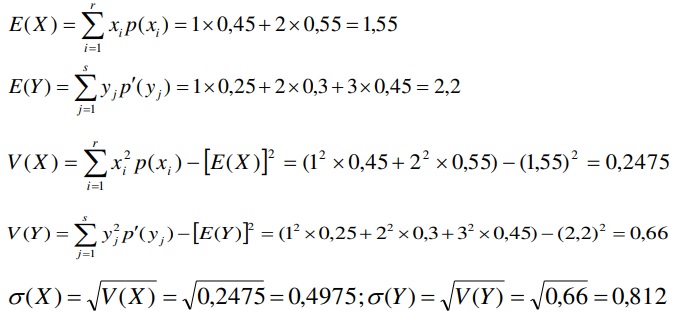
Xem thêm:
- kỳ vọng có điều kiện
- bảng phân phối fisher – snedecor | Cách tra bảng đầy đủ PDF
- bảng phân phối student | Cách tra bảng giá trị đầy đủ PDF
Bài 2: Cho biến ngẫu nhiên 2 chiều với bảng phân phối xác suất đồng thời được cho như sau:
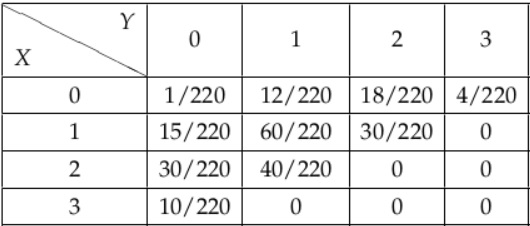
a) Hãy lập bảng phân phối xác suất thành phần của X và Y
b) Tính các số đặc trưng của các biến ngẫu nhiên thành phần X và Y.
Giải

Bài 3: Từ kết quả phân tích các số liệu thống kê trong tháng về doanh số bán hàng ( X ) và chi phí cho quảng cáo ( Y ) (đơn vị triệu đồng) của một công ty, thu được bảng phân phối xác suất đồng thời như sau:
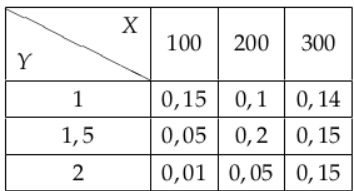
a) Tính giá trị trung bình và phương sai của doanh số bán hàng.
b) Tính giá trị trung bình và phương sai của chi phí cho quảng cáo.
Giải
Lập bảng xác suất thành phần của X và Y:

Trên đây là một số kiến thức cơ bản về phân bố xác suất thành phần của biến ngẫu nhiên rời rạc hai chiều trong môn xác suất thống kê. Hy vọng bài viết hữu ích với bạn!
Bài viết liên quan:
phân phối đều là gì? Công thức và bài tập có lời giải
phân phối mũ – Công thức tính và bài tập có lời giải
phân phối siêu bội – Công thức và bài tập có lời giải
bảng phân phối chi bình phương, Gamma | Cách tra và bài tập