Kiểm định giả thuyết thống kê là một nội dung quan trọng trong môn xác suất thống kê, giúp phân tích và đưa ra kết luận dựa trên dữ liệu mẫu. Trong bài viết này, chúng ta sẽ cùng tìm hiểu các công thức, bài tập kiểm định giả thuyết thống kê, cũng như hướng dẫn giải chi tiết để bạn nắm vững kiến thức này.
Xem thêm:
giải bài tập ước lượng khoảng tin cậy
kiểm định giả thuyết về phương sai
I. Kiểm định giả thuyết thống kê là gì?
Kiểm định giả thuyết thống kê là quá trình kiểm tra tính đúng/sai của một giả thuyết liên quan đến tham số tổng thể dựa trên dữ liệu mẫu. Quá trình này gồm các bước:
- Xây dựng cặp giả thuyết:
- Giả thuyết gốc (H₀): Giả thuyết ban đầu, được giả định đúng.
- Giả thuyết đối (H₁): Giả thuyết mâu thuẫn với H₀.
- Thu thập dữ liệu: Sử dụng mẫu ngẫu nhiên đại diện cho tổng thể.
- Lựa chọn mức ý nghĩa (α): Thông thường, mức ý nghĩa được chọn là 5% hoặc 1%.
- Áp dụng công thức kiểm định: Xác định loại kiểm định và thực hiện tính toán dựa trên dữ liệu.
- Kết luận: Dựa trên giá trị p-value hoặc thống kê kiểm định để bác bỏ hoặc chấp nhận giả thuyết.
1. Phân biệt giả thuyết và giả thiết
| Giả thuyết(Hypothesis) | Giả thiết (Assumption) |
| Cần được kiểm chứng tính đúng/ sai
Chưa được sử dụng |
Được coi là đúng
Sử dụng để suy ra điều gì đó |
2. Giả thuyết thống kê
Tham số của biến ngẫu nhiên X/ tổng thể: \(\mu, \sigma^2, p\).
Phi tham số: dạng phân phối, tính chất của X.
3. Kiểm định giả thuyết
Kiểm chứng tính đúng sai của các giả thuyết
4. Cặp giả thuyết
\(\begin{cases}H_0: \text{giả thuyết gốc } (\text{null hypothesis})\\
H_1: \text{giả thuyết đối } (\text{alternative hypothesis})\\
\end{cases}\)
Kiểm định tham số θ chưa biết, so sánh với \(\theta_0\), có 3 dạng:
\(\begin{cases}H_0: \theta = \theta_0 (\theta \le \theta_0)\\
H_1: \theta \gt \theta_0
\end{cases}\) \(\begin{cases}
H_0: \theta = \theta_0 (\theta \ge \theta_0)\\
H_1: \theta \lt \theta_0
\end{cases}\) \(\begin{cases}
H_0: \theta = \theta_0 \\
H_1: \theta\neq \theta_0
\end{cases}\)
\(\theta_0\) là 1 số biết trước => 1 tham số.
\(\theta_0\) là chưa biết trước => 2 tham số.
5. Quyết định về H0 là các sai lầm
| \(H_0\) đúng | \(H_0\) sai | |
| Bác bỏ \(H_0\) | Sai lầm loại 1. Xác suất α | Quyết định đúng. xác suất (1 – β) |
| Chấp nhận \(H_0\) | Quyết định đúng. Xác suất (1- α) | Sai lầm loại 2. Xác suất β |
II. Công thức kiểm định giả thuyết thống kê
Xét bài toán kiểm định \(\mu\) với số \(\mu_0\) biết trước:


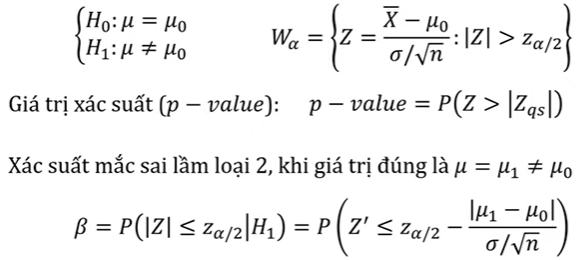

Dưới đây là các công thức quan trọng trong kiểm định giả thuyết:
1. Kiểm định trung bình tổng thể ( μ)
Trường hợp phương sai đã biết:
\(Z=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}\)Trường hợp phương sai chưa biết:
\(t=\frac{\bar{X}-\mu_0}{s/\sqrt{n}}\)2. Kiểm định tỷ lệ tổng thể (p)
\(Z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\)3. Kiểm định phương sai tổng thể (σ2)
\(\chi^{2}=\frac{(n-1)s^{2}}{\sigma^{2}_{0}}\)4. Ý nghĩa của p-value
- \(p\le \alpha\): Bác bỏ \(H_0\)
- \(p \gt \alpha\): Không đủ cơ sở bác bỏ \(H_0\)
III. Hướng dẫn giải bài tập kiểm định giả thuyết thống kê
Để giải bài tập kiểm định giả thuyết thống kê hiệu quả, bạn nên thực hiện theo các bước sau:
- Xác định bài toán: Đọc kỹ đề bài để nhận biết loại kiểm định cần thực hiện.
- Xây dựng giả thuyết: Xác định \(H_0\) và \(H_1\)
- Lựa chọn công thức kiểm định: Tùy thuộc vào dữ liệu và loại bài toán.
- Tính toán: Sử dụng công thức phù hợp để tính giá trị kiểm định hoặc p-value.
- Kết luận: So sánh kết quả với mức ý nghĩa α để đưa ra kết luận.
IV. Bài tập kiểm định giả thuyết thống kê có lời giải
Bài tập 1: Điều tra chi tiêu hàng năm của 25 công nhân khu công nghiệp A thấy trung bình là 39 triệu đồng và độ lệch chuẩn là 3,5 triệu đồng. Giả thiết chi tiêu của công nhân là biến ngẫu nhiên phân phối chuẩn.
a) Có thể cho rằng chi tiêu của công nhân khu A là 40 triệu đồng?
b) Điều tra 30 công nhân khu B thấy độ lệch chuẩn là 4 triệu đồng. Có thể cho rằng chi tiêu công nhân khu B phân tán hơn khu A không?
Giải

Bài tập 2: Trọng lượng thiết kế của một gói sữa trên dây chuyền tự động là 80gam. Người ta cân 40 gói sữa đã được sản xuất thì thu được trung bình là 79,8 gam và độ lệch chuẩn là 2.5gam. Có thể cho rằng sữa không bị đóng thiếu so với quy định
Giải

Bài tập 3: Trường X tuyển các thí sinh có năng lực học tập phù hợp, giả sử năng lực học tập được đo bởi tham số 0 và 0 ≥ 8 được cho là phù hợp. Công việc tuyển sinh được xem như kiểm định giả thuyết về năng lực học tập của thí sinh.
Giải

Bài tập 4: Điều tra chi tiêu hàng năm của 25 công nhân khu công nghiệp A thấy trung bình là 39 triệu đồng và độ lệch chuẩn là 3,5 triệu đồng. Giả thiết chi tiêu của công nhân là biến ngẫu nhiên phân phối chuẩn.
a) Có thể cho rằng chi tiêu của công nhân khu A là 40 triệu đồng? a = 5%
c) Tính p-value của kiểm định ở ý a) và xác suất mắc sai lầm loại 2 khi chi tiêu trung bình là 42 triệu đồng.
Giải

Bài tập 5: Điều tra chi tiêu hàng năm của 40 công nhân khu công nghiệp A thấy trung bình mẫu là 34 triệu đồng và độ lệch chuẩn mẫu là 5,8 triệu đồng. Điều tra công nhân tại khu công nghiệp B thì chi tiêu trung bình là 35 triệu đồng và độ lệch chuẩn là 5 triệu đồng.
Với mức ý nghĩa 5%, có thể cho rằng chỉ tiêu trung bình của công nhân khu công nghiệp A và B là như nhau không?
Tính p-value của kiểm định và cho biết kết luận thu được có thể mắc phải sai lầm loại mấy? Giả thiết chi tiêu công nhân là biến ngẫu nhiên phân phối chuẩn.
Giải


Bài tập 6: Điều tra chi tiêu hàng năm của 40 công nhân khu công nghiệp A thấy trung bình mẫu là 34 triệu đồng và độ
lệch chuẩn mẫu là 5,8 triệu đồng. Điều tra công nhân tại khu công nghiệp B thì chỉ tiêu trung bình là 35 triệu đồng và
độ lệch chuẩn là 5 triệu đồng. Giả thiết chi tiêu công nhân là biến ngẫu nhiên phân phối chuẩn.
Với mức ý nghĩa 5%, có thể cho rằng chi tiêu của công nhân khu công nghiệp B đồng đều hơn ở khu công nghiệp A
không?
Giải


Bài tập 7: Quảng cáo của một công ty cho rằng tỷ lệ phế phẩm của công ty trên thị trường tối đa là 12%. Kiểm tra 400
sản phẩm của công ty trên thị trường thì có 60 phế phẩm.
Với mức ý nghĩa 5% có thể cho rằng quảng cáo của công ty là đúng không?
Giải

Trên đây là công thức, lý thuyết về kiểm định giả thuyết trong môn xác suất thống kê. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Bài viết cùng chủ đề:
bài tập xác suất thống kê chương 1