Hệ phương trình đại số tuyến tính là một trong những kiến thức thường có trong đề thi môn toán cao cấp môn đại số và hình học giải tích. Bài viết dưới đây TTnguyen sẽ tổng hợp kiến thức cơ bản về định nghĩa , các phương pháp giải và một số dạng bài tập giải hệ phương trình tuyến tính bằng phương pháp Gauss cơ bản giúp bạn ôn tập dễ dàng.
Xem thêm:
I. Hệ phương trình tuyến tính là gì?
Định nghĩa
Hệ phương trình tuyến tính là tập hợp của hai hoặc nhiều phương trình tuyến tính có cùng biến số giống nhau. Phương trình tuyến tính có thể có một biến, hai biến hoặc ba biến. Dưới đây là dạng tổng quát của hệ với m phương trình và n ẩn:
Hệ phương trình tuyến tính tổng quát:

Trong đó:
- xi: được gọi là các ẩn của hệ
- aij: được gọi là các hệ của ẩn
- bi: được gọi là các hệ số tự do
Hệ phương trình tuyến tính thuần nhất
Nếu bi = 0 với mọi i=1,2,…,m thì hệ được gọi là hệ tuyến tính thuần nhất.
Ví dụ hệ phương trình tuyến tính thuần nhất:
\(\begin{align*}2x + 3y &= 0 \\
4x – 2y &= 0 \\
6x + y &= 0
\end{align*}\)
Cách giải hệ phương trình tuyến tính thuần nhất
Hệ phương trình tuyến tính thuần nhất chỉ có 2 trường hợp:
- Hệ có nghiệm duy nhất (nghiệm tầm thường): hạng của ma trận bằng số ẩn của hệ phương trình.
- Hệ vô số nghiệm (nghiệm không tầm thường): hạng của ma trận hệ số nhỏ hơn số ẩn của phương trình.
Ký hiệu phương trình tuyến tính dạng ma trận
Như chúng ta đã biết, hệ phương trình tuyến tính có thể viết dưới dạng ma trận. Do đó, hệ phương trình tuyến tính n biến có thể được viết dưới dạng:

II. Định lý Kronecker – Capeli
Hệ phương trình tuyến tính Ax = b có nghiệm khi và chỉ khi:
r(A)=r(Ā)
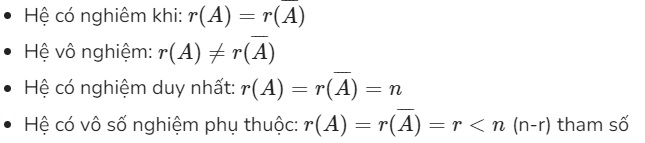
III. Phương pháp giải hệ phương trình tuyến tính
Có 4 phương pháp giải hệ phương trình tuyến tính AX = B với điều kiện khi tính định thức ma trận A ≠ 0.
- Phương pháp Cramers
- Phương pháp nghịch đảo
- Phương pháp Gauss-Jordan
- Phương pháp loại bỏ Gauss
Phương pháp Cramer mình đã có bài viết riêng, bạn có thể xem chi tiết tại đây: giải hệ phương trình bằng phương pháp cramer
Giải hệ phương trình tuyến tính bằng phương pháp ma trận nghịch đảo
Xét hệ phương trình tuyến tính AX=B là ma trận khả nghịch. Khi đó hệ có nghiệm duy nhất là:X=A-1B
Giải hệ phương trình tuyến tính bằng phương pháp Gauss
Xét hệ phương trình tuyến tính tổng quát: AX = B
Bước 1: Đưa ma trận bổ sung về dạng bậc thang bằng PBĐSC trên hàng. Ta được một hệ phương trình mới tương đương với hệ đã cho.
Bước 2: Giải hệ phương trình mới với quy tắc: Các ẩn mà các hệ số là các phần tử khác 0 đầu tiên trên các hàng của ma trận bậc thang được gọi là các ẩn ràng buộc. Các ẩn còn lại là các ẩn tự do.
IV. Bài tập hệ phương trình tuyến tính có lời giải
Một số dạng bài tập liên quan
- giải và biện luận hệ phương trình tuyến tính theo tham số m
- Nghiệm tầm thường, không tầm thường: tìm m để hệ phương trình có nghiệm duy nhất toán cao cấp
Bài tập giải hệ phương trình tuyến tính bằng phương pháp Gauss
Bài 1: Giải hệ phương trình tuyến tính sau:
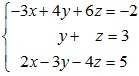
Giải
Ma trận bổ sung của hệ là:
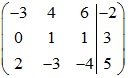
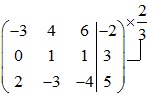
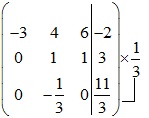
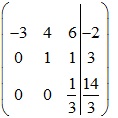
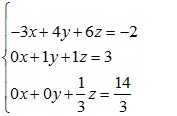
Vậy hệ phương trình có nghiệm là z=x=14; y=-11
Bài 2: Giải hệ phương trình tuyến tính bằng phương pháp gauss


Bài 3: Cách giải hệ phương trình bằng phương pháp gauss
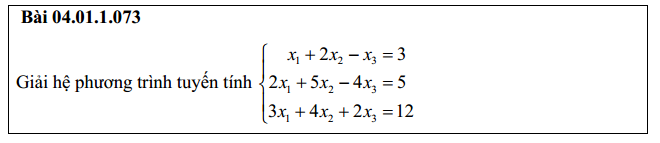

Bài 4: Cách giải hệ phương trình tuyến tính bằng phương pháp gauss
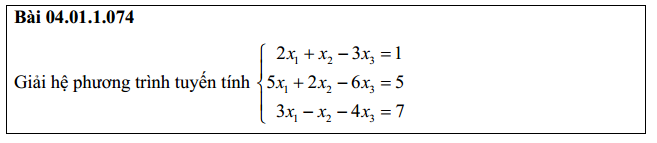

Bài 5: Giải hệ phương trình bằng phương pháp gauss
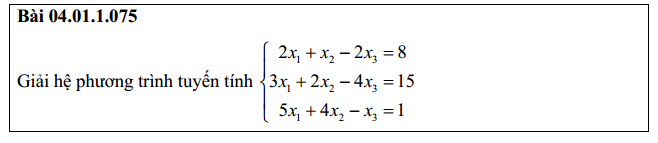

Bài 6: Giải hệ phương trình bằng phương pháp khử gauss
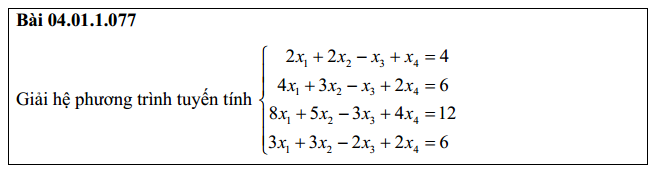

Bài 7: Giải hệ phương trình bậc nhất 3 ẩn bằng phương pháp gauss


Bài 8: Giải hệ phương trình sau bằng phương pháp gauss
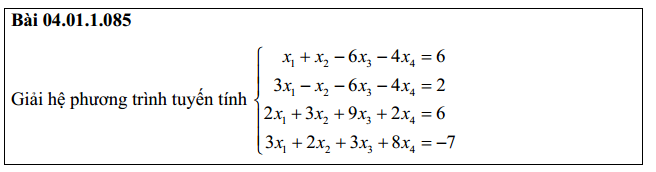

Bài 9: Giải hệ phương trình tuyến tính bằng phương pháp gauss


Bài 10: Giải phương trình tuyến tính bằng phương pháp gauss
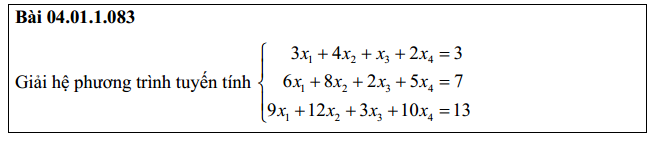

Bài 11: Phương pháp gauss giải hệ phương trình
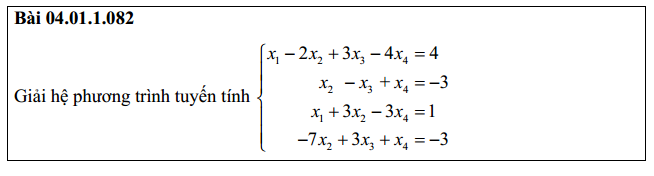

Ứng dụng hệ phương trình tuyến tính
Hệ phương trình tuyến tính được sử dụng rộng rãi trong nhiều lĩnh vực và có nhiều ứng dụng quan trọng. Dưới đây là một số ví dụ về các ứng dụng phổ biến của hệ phương trình tuyến tính:
- Kinh tế: Trong kinh tế, hệ phương trình tuyến tính được sử dụng để mô hình hóa và giải quyết các vấn đề liên quan đến tài chính, sản xuất, tiêu thụ và phân bổ tài nguyên. Ví dụ, hệ phương trình tuyến tính có thể được sử dụng để tối ưu hóa lợi nhuận trong các mô hình kinh doanh hoặc để phân tích tương quan giữa các yếu tố kinh tế.
- Kỹ thuật: Trong lĩnh vực kỹ thuật, hệ phương trình tuyến tính thường được sử dụng để mô hình hóa và giải quyết các vấn đề liên quan đến điện, cơ học, điều khiển và xử lý tín hiệu. Ví dụ, trong mạch điện, hệ phương trình tuyến tính có thể được sử dụng để tính toán dòng điện và điện áp tại các nút mạch khác nhau.
- Khoa học và kỹ thuật hóa học: Trong lĩnh vực hóa học, hệ phương trình tuyến tính thường được sử dụng để mô hình hóa và giải quyết các phản ứng hóa học và cân bằng chất lượng. Nó cũng có thể được sử dụng để tối ưu hoá quy trình sản xuất và thiết kế các hệ thống phản ứng.
Xem thêm:
- ứng dụng của đại số tuyến tính trong đời sống
- Tổng hợp công thức số phức toán cao cấp
- bài tập matlab có lời giải
Tải tài liệu bài tập cùng lý thuyết hệ phương trình tuyến tính môn đại số tuyến tính PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Ok xong trên đây là các phương pháp giải và bài tập hệ phương trình tuyến tính. Nếu có bất kì thắc mắc hoặc sai sót gì thì đừng ngần ngại liện hệ với mình nhé. Cảm ơn các bạn đã tham khảo trên ttnguyen.net