Phân phối có điều kiện và kỳ vọng có điều kiện rất hữu ích trong xác suất thống kê để giải quyết các bài toán phân tích dữ liệu, dự đoán và phân loại. Sau đây, hãy cùng TTnguyen tìm hiểu định nghĩa, bảng phân phối và cách tính cụ thể nhé!
Xem thêm:
- phân phối nhị thức là gì: Công thức và bài tập có lời giải
- phân phối poisson là gì? Công thức, quy luật và bài tập
- giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết
1. Phân phối có điều kiện là gì?
Phân phối có điều kiện là một loại phân phối xác suất mà đặc điểm của nó phụ thuộc vào một điều kiện cụ thể. Điều kiện này có thể là một giá trị hoặc một tập giá trị cho biến đang được nghiên cứu.
Ví dụ, giả sử chúng ta muốn xem xét phân phối xác suất của thời gian chuẩn bị một món ăn (biến dự báo) dựa trên tuổi của người nấu ăn (biến điều kiện). Chúng ta có thể sử dụng phân phối có điều kiện để tính toán xác suất của thời gian chuẩn bị một món ăn khi người nấu ăn có tuổi từ 30 đến 40 tuổi.
2. Kỳ vọng có điều kiện
Kỳ vọng có điều kiện là giá trị trung bình dự đoán của một biến ngẫu nhiên khi biết trước giá trị của biến khác.
Định nghĩa:
Kỳ vọng (trung bình) có điều kiện của \(Y\) khi \((X= x_{k})\)
\(E(Y | (X = x_k) = \sum_{j=1}^{s} y_j P((Y = y_j) | (X = x_k))\)
Kỳ vọng (trung bình) có điều kiện của \(X\) khi \((Y= y_{k})\)
\(E(X | (Y = y_k)) = \sum_{i=1}^r x_i P((X = x_i) / (Y = y_k))\)
Đối với biến ngẫu nhiên liên tục:
Nếu X, Y không độc lập, hay \(f(x,y)\neq f_1(x).f_2(y)\)
Ta gọi: \(f(x,y) = \frac{f(x,y)}{f_2(y)}\)
là hàm mật độ có điều kiện của X (điều kiện là Y= y)
Tương tự
\(f(x,y) = \frac{f(x,y)}{f_1(y)}\)là hàm mật độ xác suất có điều kiện của Y (điều kiện là X= x) Nếu X, Y là hai đại lượng ngẫu nhiên liên tục thì:
Kỳ vọng có điều kiện của \(Y\) khi \((X= x)\):
\(E(Y | X = x) = \int_{-\infty}^{+\infty} yf(y|x)dy\)
Kỳ vọng có điều kiện của \(X\) khi \((Y=y)\):
\( E(X | Y = y) = \int_{-\infty}^{+\infty} xf(x|y)dx \)
Hàm hồi quy:
Kỳ vọng có điều kiện của Y khi biết X = x được gọi là hàm hồi quy của Y theo x
3. Bảng phân phối xác suất có điều kiện
Bảng phân phối xác suất có điều kiện của \(X\) khi \((Y= y_{k})\):
Xác suất có điều kiện của \((X=x_i)\) khi \((Y=y_k)\), ký hiệu \(P[(X=x_i)/(Y=y_k)]\)
Bảng phân phối xác suất có điều kiện của \(Y\) khi \((X= x_{k})\):
Xác suất điều kiện của \((Y=y_i)\) khi \((X=x_k)\), ký hiệu \(P[(Y=y_i)/(X=x_k)]\)
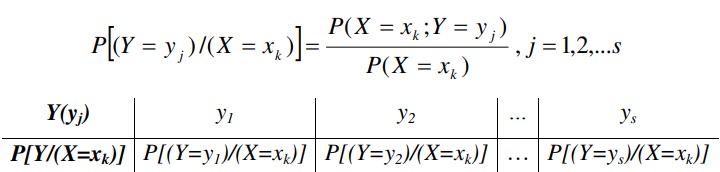
Xem thêm:
- bảng phân phối fisher – snedecor | Cách tra bảng đầy đủ PDF
- bảng phân phối student | Cách tra bảng giá trị đầy đủ PDF
4. Bài tập tính kỳ vọng có điều kiện
Cho biến ngẫu nhiên hai chiều với bảng phân phối xác suất đồng thời được cho như sau:
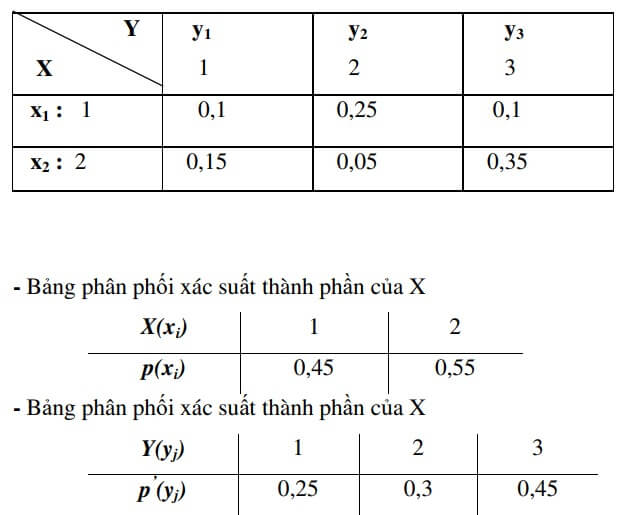
Lập bảng phân phối xác suất điều kiện của Y khi (X=1) và bảng phân phối xác suất điều kiện của X khi (Y=2). Tính kỳ vọng có điều kiện của Y khi (X=1) và kỳ vọng có điều kiện của X khi (Y=2).
Giải
– Lập bảng phân phối xác suất điều kiện
Từ đó ta có bảng phân phối xác suất điều kiện của Y khi (X=1) như sau:
Tương tự, bảng phân phối xác suất điều kiện của X khi (Y=2)
– Tính kỳ vọng có điều kiện của Y khi (X=1) và kỳ vọng có điều kiện của X khi (Y=2).
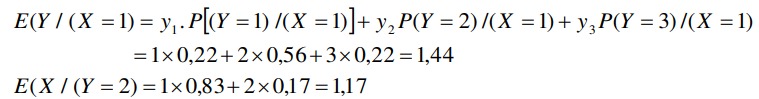
E(Y/X=x) là một hàm của x gọi là hàm hồi quy của Y theo x.
Trên đây là một số kiến thức cơ bản về phân phối, kỳ vọng điều kiện. Cảm ơn bạn đã tham khảo trên ttnguyen.net.
Tải tài liệu bảng phân phối điều kiện PDF:
Bài viết liên quan:
phân phối đều là gì? Công thức và bài tập có lời giải
phân phối mũ – Công thức tính và bài tập có lời giải
phân phối siêu bội – Công thức và bài tập có lời giải
bảng phân phối chi bình phương, Gamma | Cách tra và bài tập
