Để giải và biện luận hệ phương trình tuyến tính theo tham số m, chúng ta cần biểu diễn hệ phương trình dưới dạng ma trận và sử dụng các phép biến đổi ma trận để giải hệ.
Xem thêm:
Biện luận nghiệm của hệ phương trình tuyến tính
Cho hệ phương Ax=b là hệ có n ẩn
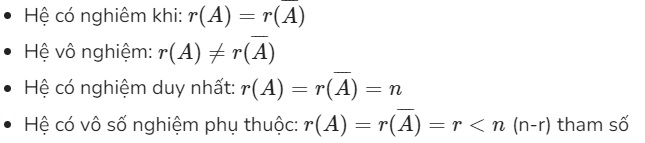
Cho hệ phương Ax=0 là hệ có n ẩn
- Hệ có nghiệm duy nhất(nghiệm tầm thường): rank(A)=n
- Hệ có vô số nghiệm(nghiệm không tầm thường): rank(A)<n
- Đối với ma trận vuông: detA= 0 => vô số nghiệm
Bài tập giải và biện luận hệ phương trình tuyến tính theo tham số m
Bài 1: Giải và biện luận hệ phương trình theo tham số m toán cao cấp
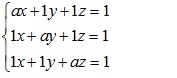
Giải
Ma trận bổ sung của hệ
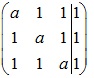
Thay đổi hàng 1 và hàng 3
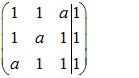
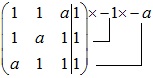
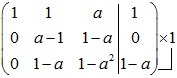
+ Với a=1 ta có
r(A)=1
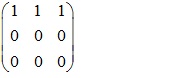
![]()
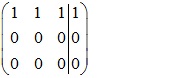
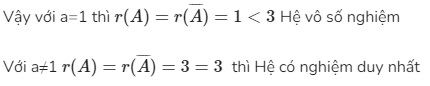
Bài viết liên quan:
Bài 2: Biện luận hệ phương trình tuyến tính
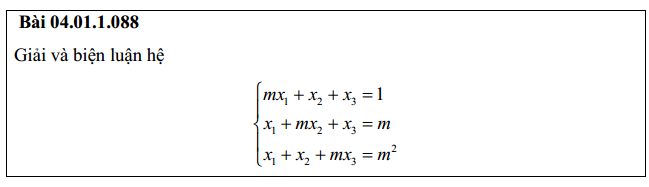

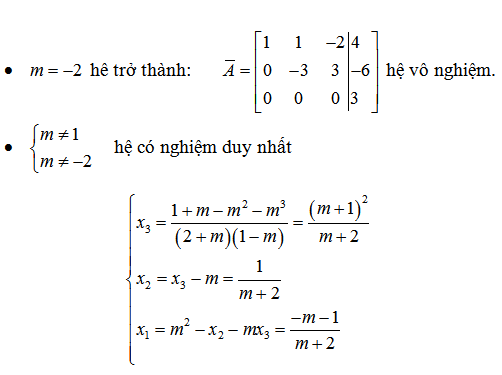
Bài 3: biện luận hệ phương trình tuyến tính theo m
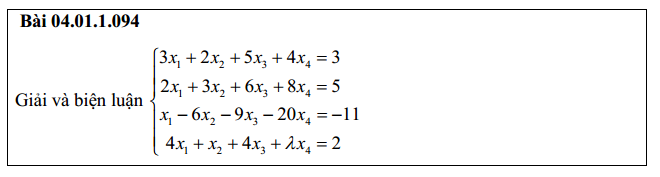

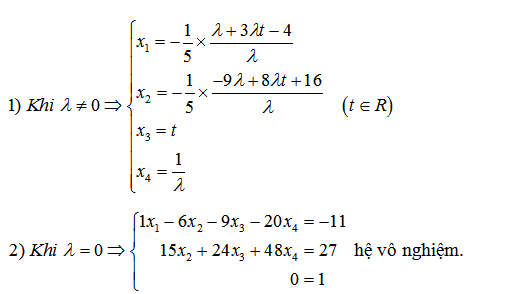
Bài 4: biện luận nghiệm hệ phương trình tuyến tính
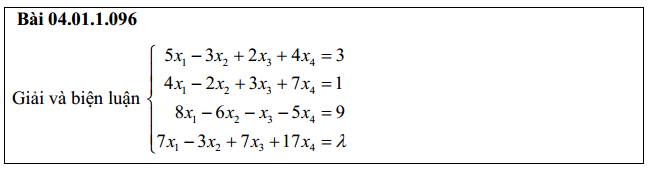

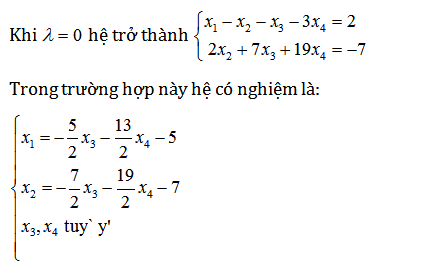
Bài 5: giải và biện luận hệ phương trình đại số tuyến tính 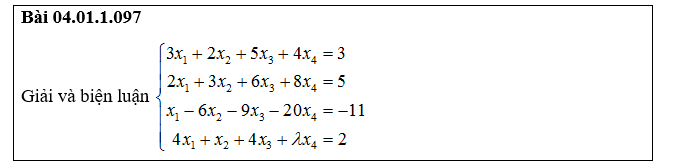

Trên đây là một số bài tập biện luận hệ phương trình tuyến tính theo tham số m trong toán cao cấp đại số tuyến tính. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Tải tài liệu giải và biện luận hệ phương trình theo tham số m toán cao cấp PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Bài viết cùng chủ đề: