Biến ngẫu nhiên rời rạc một/hai chiều – Bài tập có lời giải

Đăng vào Tác giả Nguyễn Tiến Trường

Biến ngẫu nhiên rời rạc là một biến mà giá trị của nó được xác định ngẫu nhiên trong một tập giá trị xác định trước. Trong bài viết này, hãy cùng mình tìm hiểu về khái niệm, phân loại và một số bài tập có lời giải nhé!

Xem thêm:

Khái niệm biến ngẫu nhiên – đại lượng ngẫu nhiên

Biến ngẫu nhiên là đại lượng có giá trị bằng số, nó được xác định một cách ngẫu nhiên, tùy thuộc vào mỗi kết quả của phép thử ngẫu nhiên.

Chú ý: Trong kết quả cụ thể của phép thử biến ngẫu nhiên chỉ nhận một và chỉ một giá trị.

Ký hiệu biến ngẫu nhiên

Ký hiệu biến ngẫu nhiên: \(X, Y, Z,…, X_1, X_2,…, X_k\).

Ký hiệu các giá trị của biến ngẫu nhiên: \(x, y, z,…, x_1, x_2,…, x_k\).

Ví dụ biến ngẫu nhiên

Ví dụ 1: Gọi X là số bé trai trong được sinh ra tại một bệnh viện trong một năm. X là biến ngẫu nhiên: X= 0, 1,2, …, n.

Ví dụ 2: Cho một người bắn liên tiếp từng viên đạn vào một mục tiêu, bắn cho đến viên đầu tiên trúng thì dừng. Biết xác suất bắn trung mỗi viên là p. Gọi Y là số viên đạn mà người đó đã bắn. Y là biến ngẫu nhiên: Y= 1, 2,..,n.

Ví dụ 3: Gọi Z là thời gian truy cập mạng Internet của một người trong một ngày. Z là biển ngẫu nhiên: Z∈ [0; 24].

Ví dụ 4: Với trò chơi sấp ngửa bằng cách tung đồng xu, giả sử nếu xuất hiện mặt sấp, ta được 1 đồng; nếu xuất hiện mặt ngửa, ta mất 1 đồng. Khi đó, ta có:

Phép thử t : “tung đồng xu”,

Không gian mẫu Q = {S, N},

Biến số ngẫu nhiên X với X(S) = 1 và X(N) = -1.

Xem thêm:

Phân loại biến ngẫu nhiên

Biến ngẫu nhiên rời rạc (Discrete random variable) là gì?

Khái niệm

Biến ngẫu nhiên rời rạc (Discrete random variable) Là biến ngẫu nhiên với miền giá trị là hữu hạn hoặc vô hạn đếm được.

Ví dụ về biến ngẫu nhiên rời rạc

Ví dụ 1: Số chấm xuất hiện ở mặt trên của xúc xắc; số sinh viên vắng mặt trong một buổi học; số máy hỏng trong từng ca sản xuất,… là các biến ngẫu nhiên rời rạc.

Tập giá trị của biến ngẫu nhiên rời rạc

Tập giá trị của biến ngẫu nhiên rời rạc là một tập hợp các giá trị rời rạc mà biến ngẫu nhiên có thể nhận.

Ví dụ, nếu có một biến ngẫu nhiên đếm số lượng mèo trong một hộ gia đình (một số nguyên dương), tập giá trị của biến này có thể là {0, 1, 2, 3, …}.

Một số ví dụ khác về tập giá trị của biến ngẫu nhiên rời rạc bao gồm:

– Tập giá trị của biến ngẫu nhiên tung đồng xu: {sấp, ngửa}

– Tập giá trị của biến ngẫu nhiên tung xúc xắc: {1, 2, 3, 4, 5, 6}

– Tập giá trị của biến ngẫu nhiên đếm số lượt xổ số kết quả đặc biệt trong một tuần: {0, 1, 2, 3, …}

– Tập giá trị của biến ngẫu nhiên đo điểm của học sinh trong một bài kiểm tra: {0, 1, 2, 3, …, 10}

Tùy thuộc vào tính chất của biến ngẫu nhiên, tập giá trị có thể là một tập hữu hạn hoặc vô hạn đếm được, nhưng không thể là tập giá trị vô cùng.

Biến ngẫu nhiên rời rạc hai chiều là gì?

Khái niệm

Cho X và Y là các biến ngẫu nhiên. Một véc tơ 2 chiều (X,Y) gồm hai biến ngẫu nhiên X và Y được xét đồng thời gọi là biến ngẫu nhiên 2 chiều.

Ký hiệu: (X, Y).

Ví dụ biến ngẫu nhiên hai chiều

Ví dụ : Xét kích thước của con người, đại lượng đó là một biến ngẫu nhiên hai chiều (X, Y).

Trong đó X là biến ngẫu nhiên 1 chiều: chiều cao (cm); Y là biến ngẫu nhiên 1 chiều: trọng lượng (kg).

Nếu X, Y là các biến ngẫu nhiên rời rạc thì véc tơ 2 chiều (X,Y) gọi là biến ngẫu nhiên 2 chiều rời rạc.

Biến ngẫu nhiên liên tục (Continuous random variable)

Là biến ngẫu nhiên mà các giá trị của nó lấp đầy một khoảng nào đó trên trục số. Nghĩa là miền giá trị của nó là một khoảng (hữu hạn hoặc vô hạn) của các số thực.

Dễ thấy, biến ngẫu nhiên X và Y trong ví dụ 1 và 2 là các biến ngẫu nhiên rời rạc, còn biến ngẫu nhiên Z trong ví dụ 3 là biến ngẫu nhiên liên tục.

Bài tập biến ngẫu nhiên rời rạc có lời giải

Bài 1: Trong một hộp có 10 tấm thẻ, trong đó có 4 tấm thẻ ghi số 1, 3 tấm thẻ ghi số 2, 2 tấm thẻ ghi số 3 và 1 tấm thẻ ghi số 4. Từ hộp đó rút ngẫu nhiên ra 2 tấm thẻ

a. Gọi X là số thu được khi cộng hai số ghi trên 2 tấm thẻ với nhau. Lập bảng phân phối xác suất của X

b. Gọi Y là số thu được khi nhân hai số ghi trên 2 tấm thẻ với nhau. Lập bảng phân phối xác suất của Y

Giải

a.
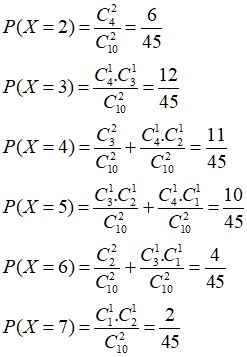
Bài tập bảng phân phối xác suất 12

-Bảng phân phối xác suất của X

X 2 3 4 5 6 7
P 6/45 12/45 11/45 10/45 4/45 2/45

b.

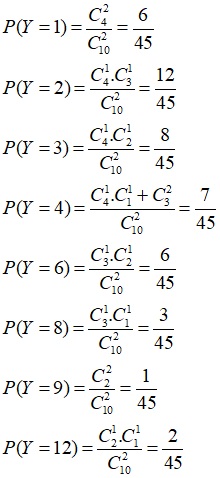
Bài tập bảng phân phối xác suất 13

-Bảng phân phối xác suất của Y

Y 1 2 3 4 6 8 9 12
P 6/45 12/45 8/45 7/45 6/45 3/45 1/45 2/45

Bài 2: Một cơ quan có 3 xe ôtô : 1 xe 4 chỗ; 1 xe 50 chỗ và 1 xe tải. Xác suất để trong một ngày làm việc, các xe được xử dụng là 0,8; 0,4 và 0,9. Hãy lập bảng phân phối xác suất cho số xe được xử dụng trong một ngày của cơ quan.

Bài tập biến ngẫu nhiên rời rạc

Phân biệt biến ngẫu nhiên rời rạc và liên tục

Biến ngẫu nhiên rời rạc Biến ngẫu nhiên liên tục
Là biến ngẫu nhiên có tập giá trị có số hữu hạn hoặc đếm được Là biến ngẫu nhiên có tập giá trị liên tục, tức là không đếm được và có thể là bất kỳ giá trị nào trên một khoảng số thực.
Kết quả của biến ngẫu nhiên rời rạc là các giá trị riêng lẻ. Kết quả của biến ngẫu nhiên liên tục là một giá trị nằm trong một khoảng giới hạn.
Ví dụ, số lần tung xúc xắc để ra kết quả 6, số xe ô tô đi qua một ngã tư trong một khoảng thời gian nhất định. Ví dụ, chiều cao của một người, thời gian chạy một vòng đua, nhiệt độ trong một phòng là những.

Tóm lại, biến ngẫu nhiên rời rạc có tập giá trị rời rạc và kết quả của nó là các giá trị riêng lẻ, trong khi biến ngẫu nhiên liên tục có tập giá trị liên tục và kết quả của nó nằm trong một khoảng giới hạn.

Tải tài liệu biến ngẫu nhiên PDF:

Hy vọng bài viết này hữu ích với bạn. Cảm ơn bạn đã tham khảo xác suất thống kê trên ttnguyen.net.

Bài viết liên quan:

Nguyễn Tiến Trường

Mình viết về những điều nhỏ nhặt trong cuộc sống, Viết về câu chuyện những ngày không có em