Để giúp các bạn nắm vững kiến thức phần lập bảng phân phối xác suất. Trong bài viết này, chúng ta sẽ tìm hiểu cách lập bảng phân phối xác suất, các tính chất thông qua một số bài tập minh hoạ.
Xem thêm:
- Phân phối nhị thức là gì: Công thức và bài tập có lời giải
- Phân phối Poisson là gì? Công thức, quy luật và bài tập
- Phân phối xác suất thành phần – Các đặc trưng và bài tập
1. Tổng quan về bảng phân phối xác suất
1.1. Định nghĩa hàm xác suất
Cho biến ngẫu nhiên rời rạc X với các giá trị có thể là \(x_1, x_2,..,x_n\).
Hàm xác suất của biến ngẫu nhiên rời rạc X, ký hiệu P(x) được xác định như sau:
\(p(x) = P(X=x)\) với \(x = x_1, x_2,..,x_n\).
1.2. Tính chất của hàm xác suất
\((1)p(x)\ge 0 \\(2)\sum p(x_i) = 1\)
1.3. Ví dụ hàm xác suất
Ví dụ: Gieo con xúc xắc cân đối và đồng chất 1 lần. Gọi X là số chấm xuất hiên. X là biến ngẫu nhiên rời rạc với các giá trị 1, 2, … ,6. Khi đó hàm xác suất tương ứng là:
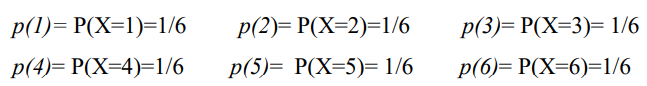
2. Cách lập bảng phân phối xác suất
2.1. Định nghĩa bảng phân phối xác suất
Bảng phân phối xác suất chuẩn dùng để thiết lập luật phân phối xác suất của đại lượng ngẫu nhiên rời rạc.
Bảng gồm 2 dòng:
- Dòng trên ghi các giá trị có thể có của đại lượng ngẫu nhiên là: \(x_1, x_2,..,x_n\);
- Dòng dưới ghi các xác suất tương ứng là: \(P_1, P_2,..,P_n\).
| \(X(x_i)\) | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | \(x_5\) | \(x_n\) |
| \(P(x_i)\) | \(P(x_1)\) | \(P(x_2)\) | \(P(x_3)\) | \(P(x_4)\) | \(P(x_5)\) | \(P(x_n)\) |
2.2. Tính chất bảng phân phối xác suất
Từ tính chất của hàm xác suất ta có:
- \(0\le p(xi)\le 1\)
- \(p(x_1)+p(x_2)+…+p(x_k)=1\)
2.3. Đồ thị phân phối xác suất
– Biểu diễn các giá trị có thể của biến ngẫu nhiên nằm trên trục ngang (trục hoành).
– Biểu diễn các xác suất của các biến cố tương ứng với các giá trị đó nằm trên trục thẳng đứng (trục tung). Khi đó đồ thị xác suất được biểu diễn bởi đoạn thẳng (thanh thẳng đứng) mà độ cao của nó bằng xác suất.
2.4. Các lập bảng phân phối xác suất
Để lập bảng phân phối xác suất, bạn thực hiện theo các bước sau:
- Xác định biến ngẫu nhiên và các giá trị có thể nhận được: Dựa trên bài toán, xác định tất cả các kết quả khác nhau mà biến ngắu nhiên có thể nhận.
- Tính xác suất tương ứng với mỗi giá trị: Sử dụng các quy tắc xác suất hoặc tính đến tần suất xảy ra của từng giá trị.
- Kiểm tra điều kiện xác suất: Tổng tất cả các xác suất phải bằng 1.
- Lập bảng phân phối xác suất.
Xem thêm:
- Phân phối xác suất có điều kiện và kỳ vọng có điều kiện
- Phân phối xác suất đồng thời – Cách lập bảng có đáp án
3. Hàm phân phối tích lũy
3.1. Định nghĩa
Hàm phân phối xác suất (hàm phân phối tích lũy) của biến ngẫu nhiên rời rạc X, ký hiệu là \(F(x)\).
3.2. Biểu thức
Nếu biến ngẫu nhiên rời rạc X với các giá trị có thể là \(x_1, x_2,…,x_k\) và các xác suất tương ứng là \(p(x_1)+p(x_2)+…+p(x_k)\) thì biểu thức cụ thể của hàm phân phối tích lũy được cho như sau:
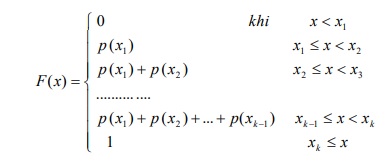
3.3. Đồ thị hàm phân phối tích lũy
Hàm phân phối tích lũy của biến ngẫu nhiên rời rạc là hàm không liên tục (gián đoạn tại các giá trị có thể của nó). Đồ thị của hàm phân phối tích lũy có dạng hình bậc thang.
4. Kỳ vọng, Phương sai và Độ lệch chuẩn
4.1. Kỳ vọng E(X)
Kỳ vọng (giá trị trung bình) của X là , ký hiệu là E(X) hoặc μ là:


4.2. Phương sai
Phương sai của biến ngẫu nhiên rời rạc X, ký hiệu σ2 hay V(X) là giá trị trung bình trọng số (kỳ vọng) của bình phương các sai lệch giữa các giá trị x1, x2, … ,xk của biến ngẫu nhiên X với giá trị trung bình μ của nó:

4.3. Độ lệch chuẩn
Độ lệch chuẩn của X, ký hiệu σ (X), là:
![]()

Xem thêm:
- Phân phối Fisher – snedecor | Cách tra bảng đầy đủ PDF
- Phân phối t-Student | Cách tra bảng giá trị đầy đủ PDF
- Phân phối đều là gì? Công thức và bài tập có lời giải
Ví dụ tính kỳ vọng, phương sai và độ lệch chuẩn:

4.4. Ý nghĩa của kỳ vọng và phương sai
Ý nghĩa kỳ vọng:
- Kỳ vọng toán phản ánh giá trị trung tâm của phân phối xác suất của biến ngẫu nhiên.
- Trong kinh tế, kỳ vọng toán đồng thời mang 2 ý nghĩa:
- Nếu xét trong 1 số lớn phép thử tương tự thì nó phản ánh giá trị trung bình
- Nếu xét trong 1 phép thử đơn lẻ thì nó phản ánh giá trị mong đợi.
Ý nghĩa phương sai :
- Phương sai phản ánh mức độ phân tán của các giá trị của biến ngẫu nhiên so với giá trị trung bình.
- Phương sai càng lớn: phân tán càng nhiều quanh giá trị trung bình còn phương sai càng nhỏ: giá trị càng tập trung quanh giá trị trung bình.
- Trong kinh tế, phương sai phản ánh mức độ rủi ro hay độ biến động (kém ổn định).
5. Các bài tập về bảng phân phối xác suất
5.1. Bài tập phân phối xác suất có lời giải
Bài 1: Cho biến ngẫu nhiên rời rạc X với bảng phân phối xác suất được cho như sau:
| X | -2 | -1 | 0 | 1 | 2 |
| P(X) | 1/8 | 2/8 | 2/8 | 2/8 | 1/8 |
a) P(X ≤ 2); P(X>-2); P(-1≤ X≤1);P(X ≤ -1 hoặc X=2).
b) Xác định hàm phân phối tích lũy và tính các xác suất sau: P(X≤1.25);P(X≤2.2).
c) Tính kỳ vọng và phương sai của X.
Giải
a.
P(X)=1/8+2/8+2/8+2/8+1/8=1
P(X>-2)=2/8+2/8+2/8+1/8=7/8
P(-1≤ X≤1)=2/8+2/8+2/8=6/8
P(X ≤ -1 hoặc X=2)=1/8+2/8+1/8=1/2
b.Hàm phân phối tích luỹ:
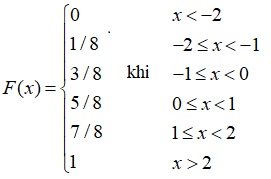
Vậy P(X≤1.25)=7/8; P(X≤2.2)=1
c. Kỳ vọng và phương sai của X
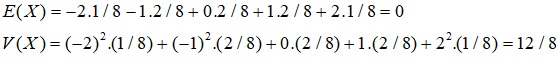
5.2. Bài tập lập bảng phân phối xác suất
Bài 2: Một nhân viên kỹ thuật của một công ty đã đưa ra một sản phẩm mới. Công ty ước tính nếu đưa sản phẩm ra thị trường thì xác suất rất thành công là 0.6, xác suất thành công là 0.3 và xác suất không thành công là 0.1. Thu nhập tương ứng cho các trường hợp này là 15 triệu đô la, 5 triệu đô la và – 500 000 đô la. Gọi X là biến ngẫu nhiên thu nhập nhận được.
a) Lập bảng phân phối xác suất của biến ngẫu nhiên
b) Xác định hàm phân phối tích lũy của X.
c) Xác định kỳ vọng phương sai và độ lệch chuẩn của X.
Giải
a. Hàm xác suất thu nhập nhận được là:
| X | -500 000 | 5 triệu | 15 triệu |
| P | 0.1 | 0.3 | 0.6 |
b. Hàm phân phối tích luỹ

c. Kỳ vọng
E(X)=-500000.0.1+5000000.0.3
+15000000.0.6=10450000
V(X)=[(-500000)^2.0.1+(5000000)^2.0.3+(15000000)^2.0.6]-(10450000)^2=3.33×10^13
Độ lệch chuẩn của X là sqrt(3.33×10^13)
5.3. Bài tập tính kỳ vọng và phương sai có lời giải
Bài 3: Một nhóm học sinh có 10 em, trong đó có 3 em học loại giỏi, 4 loại khá, còn lại là trung bình. Từ nhóm đó chọn ngẫu nhiên ra 3 học sinh. Gọi X là số học sinh giỏi trong số học sinh chọn ra
a. Lập bảng phân phối xác suất của X
b. Viết biểu thức hàm phân phối xác suất của X
c. Tính kỳ vọng, phương sai của X
d. Tính xác suất để trong số học sinh chọn ra có ít nhất 1 học sinh giỏi
Giải
a. Ta có
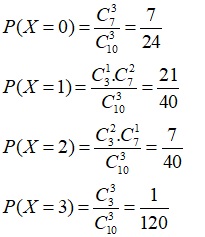
Bảng phân phối xác suất:
| X | 0 | 1 | 2 | 3 |
| P | 7/24 | 21/40 | 7/40 | 1/120 |
b.Hàm phân phối xác suất

c. Kỳ vọng: E(X)=0.7/24+21/40+2.7/40+3.1/120=9/10
V(X)=[(0)^2.7/24+(1)^2.21/40+(2)^2.7/40+(3)^2.1/120]-(9/10)^2=67/50
d. Xác suất để chọn ra ít nhất 1 học sinh giỏi là: 21/40+2.7/40+3.1/120=9/10
5.4. Bài tập hàm phân phối xác suất tích lũy
Bài 4: Một siêu thị có 3 chuông báo cháy hoạt động độc lập với nhau. Xác suất làm việc tốt (chuông kêu khi có cháy) trong 1 năm của mỗi chuông lần lượt là 0,7; 0,8; 0,9. Gọi X là số chuông kêu khi có cháy trong một năm tới ở siêu thị đó.
a) Lập bảng phân phối của X
b) Viết biểu thức hàm phân phối tích luỹ của X
c) Tính kỳ vọng và phương sai của X
Giải
Gọi A là biến cố chuông I kêu khi có cháy
B là biến cố chuông II kêu khi có cháy
C là biến cố chuông III kêu khi có cháy
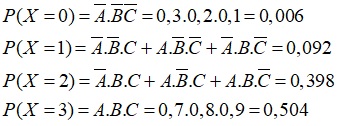
=> a.Bảng phân phối xác suất
| X | 0 | 1 | 2 | 3 |
| P | 0,006 | 0,092 | 0,398 | 0,504 |
b. hàm phân phối tích luỹ

c. Kỳ vọng E(X)=0.0,006+1.0,092+2.0,398+3.0,504=2,4 ; phương sai V(X)=0,46
5.5. Bài tập tìm hàm phân phối xác suất
Bài 5: Một người đi từ nhà đến cơ quan phải qua 3 ngã tư, xác suất gặp đèn đỏ ở các ngã tư đều bằng 0,4. Gọi X là số ngã tư mà người đó gặp đèn đỏ.
a. Lập bảng phân phối xác suất của X.
b. Viết biểu thức hàm phân phối tích luỹ của X.
c. Tính kỳ vọng, phương sai của X.
d. Nếu mỗi lần gặp đèn đỏ người ấy phải đợi khoảng 1,2 phút thì thời gian trung bình phải dừng trên đường là bao nhiêu?
Giải
Bài toán là dãy phép thử bernoulli n=3 ; p=0,4 ; q=0,6
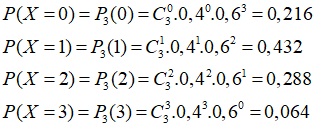
a. Bảng phân phối xác suất
| X | 0 | 1 | 2 | 3 |
| P | 0,216 | 0,432 | 0,288 | 0,064 |
b.Biểu thức phàm phân phối tích luỹ của X là:

c. Kỳ vọng E(X)=1,2 ; Phương sai V(X)=0,72
d.Gọi Y là thời gian dừng đèn đỏ
X=0=>Y=0 =>P(Y)=0,216
X=1=>Y=1,2 =>P(Y)=0,432
X=2=>Y=2,4 =>P(Y)=0,288
X=3=>Y=3,6 =>P(Y)=0,064
Thời gian trung bình phải dừng trên đường là:
E(Y)=0.0,216+1,2.0,432+0,288.2,4+3,6.0,064=1,44.
5.6. Bài tập tìm quy luật phân phối xác suất
Bài 8: Một người có 5 viên đạn dùng để thử súng. Người đó bắn từng viên cho đến khi trúng tâm thị dừng bắn. Biết rằng xác suất bắn trúng tâm của người đó bằng 0,9.
a) Tìm quy luật phân phối xác suất của X – Số viên đạn đã tiêu thụ.
b) Tính kỳ vọng và phương sai của X.
c) Gọi Y là số viên đạn còn thừa. Tìm quy luật phân phối xác suất của Y.
Giải
A là biến cố bắn trúng
\(\overline{A}\) là biến cố bắn trượt
TH1: bắn trúng 1 viên: P1=A=0,9
TH2: bắn trúng 2 viên: P2=\(\overline{A}A\)=0,1.0,9=0,09
TH3: bắn trúng 3 viên: P3=\(\overline{AA}A=0,1^2.0,9=0,09\)
TH4: bắn trúng 4 viên: P4=\(\overline{AAA}A=0,1^3.0,9=0,009\)
TH5: bắn trúng 5 viên: P5=\(\overline{AAAA}A+\overline{AAAAA}
=0,0004\)
– Tỷ lệ của bảng phân phối X
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0,9 | 0,09 | 0,009 | 0,0009 | 0,0001 |
b. Kỳ vọng E (X) = 1,0786; Phương sai V (X) = 0,26634
c.
TH1: P (Y = 0) = P (X = 5) = 0,0001
TH2: P (Y = 1) = P (X = 4) = 0,0009
TH3: P (Y = 2) = P (X = 3) = 0,009
TH4: P (Y = 3) = P (X = 2) = 0,09
TH5: P (Y = 4) = P (X = 1) = 0,9
– Tỷ lệ của bảng phân phối Y
| Y | 0 | 1 | 2 | 3 | 4 |
| P | 0,0001 | 0,0009 | 0,009 | 0,09 | 0,9 |
Tải tài liệu hàm phân phối xác suất thống kê PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Ok xong, trên đây là toàn bộ bài tập về lập bảng phân phối xác suất thống kê, tính kỳ vọng, phương sai, độ lệch chuẩn của biến ngẫu nhiên rời rạc. Cảm ơn bạn đã tham khảo tài liệu trên TTnguyen.
Bài viết liên quan:
- Phân phối mũ – Công thức tính và bài tập có lời giải
- Phân phối siêu bội – Công thức và bài tập có lời giải
- Bảng phân phối chi bình phương, Gamma | Cách tra và bài tập
- Giải bài tập xác suất thống kê chương 2 – Tổng hợp chi tiết