Xác suất có điều kiện là khả năng xảy ra của một biến cố, dựa trên việc một biến cố khác đã xảy ra. Trong bài viết này, TTnguyen sẽ cùng bạn tìm hiểu lý thuyết, công thức tính và một số bài tập xác suất có điều kiện trong môn xác suất thống kê giúp bạn nắm vững kiến thức phần này nhé.
Xem thêm:
1. Xác suất có điều kiện là gì?
Xác suất có điều kiện (Conditional probability) được ký hiệu là \(P(A|B)\), nghĩa là xác suất xảy ra biến cố A, với điều kiện biến cố B đã xảy ra.
Ký hiệu:
- \(P(A|B)\): Xác suất của A, biết rằng B đã xảy ra (đọc là “xác suất của A, biết B“).
- \(P(A\cap B)\): Xác suất A và B xảy ra đồng thời.
2. Công thức tính xác suất có điều kiện
Công thức tổng quát của xác suất có điều kiện là:

Trong đó biến cố A đã xảy ra trước, còn biến cố B xảy ra sau và P(A) >0.
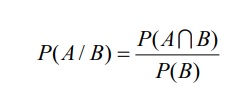
Trong đó biến cố B đã xảy ra trước, còn biến cố A xảy ra sau và P(B) >0. Trường hợp đặc biệt khi không gian mẫu có các kết quả đồng khả năng thì:
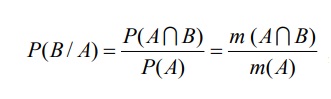
Trong đó m (A∩B)là số các trường hợp thuận lợi của (A∩B); m(A) là số các trường hợp thuận lợi của A.
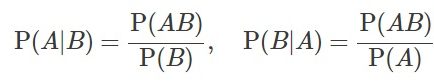
Một số khái niệm quan trọng trong xác suất có điều kiện:
- Hai biến cố A và B được gọi là độc lập nếu: \(P(A|B)=P(A)\) hoặc \(P(B|A)=P(B)\).
- Biến cố phụ thuộc: \(P(A|B)\neq P(A)\)
3. Ví dụ xác suất điều kiện
Ví dụ : Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6. Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm.
Ký hiệu A là biến cố “con xúc xắc thứ nhất xuất hiện mặt 4 chấm” và B là biến cố “ Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”. Như vậy A xảy ra trước B.
Khi con xúc xắc xuất hiện mặt 4 chấm (biến cố A đã xảy ra) thì xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6 được gọi là xác suất điều kiện của biến cố B khi biến cố A đã xảy ra. Ký hiệu là P(B/A).
Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì không gian mẫu sẽ chỉ còn 6 kết quả (6 biến cố) sau đây: (4,1); (4,2); (4,3); (4,4); (4,5); (4,6).
Suy ra P(B/A) = P(4,2)=1/6 .
4. Phân biệt xác suất thông thường và xác suất có điều kiện
Một trong những các dễ dàng nhất để nhận biết xác suất thông thường hay xác suất có điều kiện là:
| Xác suất thông thường | Xác suất có điều kiện |
| Không dựa trên bất kỳ điều kiện nào. | Câu hỏi chứa từ khoá: biết rằng, nếu, khi,… VD: Biết công ty thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2.
Đề bài cho lần lượt khả năng A, B. VD: Khả năng thắng thầu của các dự án lần lượt là 0,4 và 0,5. |
Xem thêm:
5. Các dạng bài tập xác suất có điều kiện
5.1 Tính xác suất có điều kiện các biến cố độc lập
Bài 1: Một công ty đấu thầu 2 dự án độc lập. Khả năng thắng thầu của các dự án lần lượt là 0,4 và 0,5.
a)Tìm xác suất công ty thắng thầu đúng 1 dự án.
b) Biết công ty thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2.
c) Biết công ty không thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2.
Giải
Gọi A là biến cố”thắng thầu dự án 1″
B là biến cố”thắng thầu dự án 2″ mà theo đề bài P(A)= 0,4 , P(B)=0,5, 2 biến cố A,B độc lập
a) Gọi A1 là biến cố “thắng thầu đúng 1 dự án”
\(P(A1)=P(A \overline{B}+ \overline{A}B)\)
\(= P(A \overline{B}) +P(\overline{A}B)\)
\(P(A1)=P(A).P( \overline{B})+ P(\overline{A})P(B)\)
\(= 0,4.(1-0,5)+ (1-0,4).0,5=0,5\)
b) Gọi B1 là biến cố “thắng thầu dự án thứ 2 biết thắng thầu dự án 1”
P(B1)=P(B|A)= P(B)=0,5 (do A,B là hai biến cố độc lập)
c) Gọi C1 là biến cố “thắng thầu dự án 2 biết không thắng thầu dự án 1”
\(P(C1)=P(B|\overline{A})=P(B)=0,5\)5.2 Tính xác suất điều kiện các biến cố bất kỳ
Bài 2: Một công ty đấu thầu 2 dự án. Khả năng thắng thầu của các dự án lần lượt là 0,4 và 0,5. Khả năng thắng thầu của 2 dự án là 0,3. Gọi A, B lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) A và B có độc lập không?
b) Tìm xác suất công ty thắng thầu đúng dự án 1.
c) Biết công ty thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2.
d) Biết công ty không thắng thầu dự án 1, tìm xác suất công ty thắng thầu dự án 2.
Giải
Tóm tắt đề bài: P(A)=0,4 , P(B)=0,5 , P(AB)=0,3
a) A,B độc lập => P(AB)= P(A).P(B)
mà 0,3 ≠0,4×0,5 => A, B không độc lập (phụ thuộc)
b) Gọi B1 là biến cố thắng thầu đúng 1 dự án
\(P(B1)=P(A\overline{B})+P(\overline{A}B)\)
\(=P(A)-P(AB)+P(B)-P(AB)\)
\(=P(A)+P(B)-2P(AB)=0,3\)
c) Gọi C1 là biến cố thắng dự 2 biết thắng dự án 1
\(P(C1)=P(B|A)=\frac{P(AB)}{P(A)}=\frac{0,3}{0,4}=0,75\)d) Gọi D1 là biến cố “thắng dự án 2 biết không thắng dự án 1”
\(P(D1)=P(B|\overline{A})=\frac{P(\overline{A}B)}{P(\overline{A})}=\frac{P(B)-P(AB)}{1-P(A)}\)
\(=\frac{0,5-0,3}{1-0,4}=\frac{1}{3}\)
5.3 Cách tính xác suất có điều kiện
Bài 3: Một sinh viên làm 2 bài tập kế tiếp. Xác suất làm đúng bài thứ nhất là 0,7. Nếu làm đúng bài thứ nhất thì khả năng làm đúng bài thứ 2 là 0,8, nhưng nếu làm sai bài thứ 1 thì khả năng làm đúng bài thứ 2 là 0,2. Tính xác suất:
a) Làm đúng ít nhất 1 bài.
b) Làm đúng bài 1 biết rằng làm đúng bài 2.
c) Làm đúng cả 2, biết rằng làm đúng một bài.
Giải
Gọi A1 là biến cố làm đúng bài 1
Gọi A2 là biến cố làm đúng bài 2
a) Làm đúng ít nhất 1 bài
\(P(A1+A2)= 1-P(\overline{A1+A2})\)
\(= 1-P(\overline{A1}.\overline{A2})\)
\(=1-P(\overline{A1})P(\overline{A2}|\overline{A1})=0,76\)
b) Làm đúng bài 1 biết rằng làm đúng bài 2
\(P(A1.A2)= P(A1).P(A2|A1)=0,7.0,8\)
\(P(A1+A2)= P(A1)+P(A2)-P(A1A2)\)
\(0,76= 0,7+P(A2)- 0,7.0,8\)
\(=>P(A2)=0,62\)
\(P(A1|A2)= \frac{P(A1A2)}{P(A2)}\)
\(=\frac{P(A1)P(A2|A1)}{P(A2)}=0,903\)
c) Làm đúng cả 2 biết rằng làm đúng ít nhất 1 bài
\(P(A1A2|(A1+A2))= \frac{P[(A1A2).(A1+A2)]}{P(A1+A2)}\)
\(= \frac{P[(A1A1A2)+(A1A2A2)]}{P(A1+A2)}\)
\(=\frac{P[(A1A2)+(A1A2)]}{P(A1+A2)}\)
\(= \frac{P(A1A2)}{P(A1+A2)}=0,737\)
Tải tài liệu xác suất điều kiện PDF miễn phí:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Hy vọng qua bài viết trên đã cung cấp cho bạn đủ thông tin giúp bạn giải bài tập xác suất có điều kiện một cách dễ dàng nhất. Cảm ơn các bạn đã tham khảo tài liệu trên ttnguyen.net.
Bài viết liên quan:
bài toán lấy ngẫu nhiên có hoàn lại