Trong bài viết này, chúng ta sẽ giải một phương trình bậc 2 số phức cụ thể. Qua việc giải phương trình này, chúng ta sẽ áp dụng các công thức và phép tính phức để tìm ra giá trị phức của biến số mà thỏa mãn phương trình.
Bài viết liên quan:
- căn bậc 2 của số phức
- bài tập số phức toán cao cấp có lời giải
- Tổng hợp công thức số phức toán cao cấp
1. Phương trình bậc 2 số phức
Phương trình bậc 2 số phức là một phương trình toán học có dạng \(ax^2 + bx + c = 0\), trong đó a, b và c là các số phức và x là biến số phức. Để giải phương trình này, ta sử dụng công thức giải phương trình bậc 2 số phức, tương tự như giải phương trình bậc 2 số thực.
2. Cách giải phương trình bậc 2 số phức
Cho phương trình bậc hai \(ax^2+bx+c=0\) với a, b, \(c \in \mathbb{R}\), \(a \neq 0\)
Xét \(\Delta = b^2 – 4ac\) ta thấy:
- Khi \(\Delta = 0\) thì phương trình có 1 nghiệm thực \(\frac{-b }{2a}\)
- Khi \(\Delta > 0\) thì phương trình có 2 nghiệm thực phân biệt \(x_{1, 2} = \frac{-b \pm \sqrt{ \Delta } }{2a}\)
- Khi \(\Delta < 0\) thì phương trình có 2 nghiệm thực phân biệt \(x_{1, 2} = \frac{-b \pm i \sqrt{ |\Delta| } }{2a}\)
Hệ thức vi-et vẫn đúng trong trường số phức: \(z_1 + z_2 = \frac{-b}{a}\) và \(z_1.z_2 = \frac{c}{a}\)
Xem thêm: số phức nghịch đảo
Giải phương trình số phức bằng máy tính
Ví dụ giải phương trình ![]() bằng máy tính
bằng máy tính
Bước 1: Bấm Mode 2 để chuyển sang số phức
Bước 2: Bấm (1+i)x + (2-3i)conjg(x)-3+4i. Tiếp theo bấm 1000+0.01i và bấm “=”.

Bước 3: Đến đây ta phân tích phần thực của kết quả vừa thu được theo 2 số 1000 và 0.01. Ta được: 2996,96=3.1000-4.0,01-3 và -1996,01=-2.1000-0,01+4.
Từ đó ta thu được hệ: 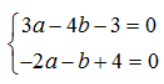
Bước 4: Vào chức năng MODE 9 để giải hệ phương trình bậc nhất 2 ẩn ta thu được kết quả.
Bài tập giải phương trình bậc 2 số phức
Giải phương trình bậc 2 số phức
Câu 1. Nghiệm phức có phần ảo dương của phương trình \(z^2-2z+5=0\) là
Lời giải
Bước 1: Tính \(\Delta’ = b’^2 \: – \: ac = 1 \: – \: 5 = -4 < 0\)
Bước 2: Vì \(\bigtriangleup <0\) nên phương trình có 2 nghiệm phức phân biệt là \(z_{1,2} = 1 \pm 2i\)
Bước 3: Theo đề số phức có phần ảo dương nên do đó z = 1 + 2i
Câu 2. Gọi \(z_0\) là nghiệm phức có phần ảo dương của phương trình \(z^2 + 6z + 13 = 0\). Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(1 \: – \: z_0\) là
Lời giải
Ta có: \(z^2 + 6z + 13 = 0\)
Xét \(\Delta’ = b’^2 \:-\: ac = -4\)
Vì \(\Delta’ < 0 \)nên phương trình có 2 nghiệm phức \(z_{1,2} = -3 + 2i\)
Theo đề \(z_0\) là nghiệm phức có phần ảo dương của phương trình nên \(z_0 = -3 + 2i\)
Suy ra: \(1 \:-\: z_0 = 4 \:-\: 2i\)
Vậy điểm biểu diễn theo yêu cầu bài toán là P(4;-2)
Câu 3. Phương trình nào dưới đây nhận hai số phức 1 + \(\sqrt{2}i\) và \(1 \:-\: \sqrt{2}i\) là nghiệm
Lời giải
Theo định lý viet ta có: \(\left\{\begin{matrix}z_1+z_2=2 \\z_1.z_2 = 3 \end{matrix}\right.\), do đó \(z_1, z_2\) là hai nghiệm của phương trình \(z^2 \:-\:2z + 3 = 0\)
Câu 4: Phương trình \((z^2 + i)(z^2- 2iz – 1) = 0\) có nghiệm là:
Lời giải
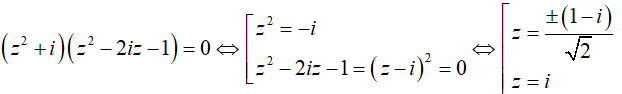
Câu 5: Giải phương trình sau:![]()
Lời giải:
Giả sử z=a+bi (a,b∈R) thay vào phương trình đã cho và biến đổi ta được:
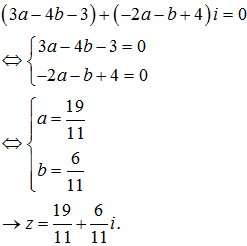
Câu 6: Gọi \(z_1, z_2\) là hai nghiệm của phương trình \(z^2 + 2z + 10 = 0\). Tính giá trị của biểu thức \(A = |z_1|^2 + |z_2|^2\)
Ta có: \(z^2+2z+10 = 0\)
Xét \(\Delta’ = b’^2 – ac = 1 \: – \: 10 = -9\)
Vì \(\Delta’ < 0\) nên phương trình có nghiệm phức phân biệt
Theo công thức đã nêu ở trên thì ta có \(z_{1,2} = -1\pm 3i\)
Vậy \(A = |z_1|^2 + |z_2|^2 = |-1-3i|^2 + |-1+3i|^2 = 20\)
Xem thêm: số phức liên hợp của số phức
Giải phương trình số phức bậc 3
Câu 1: Nghiệm của phương trình \(z^{3} – 8 = 0\) là :
Lời giải:
Sử dụng hằng đẳng thức số 7, ta có:
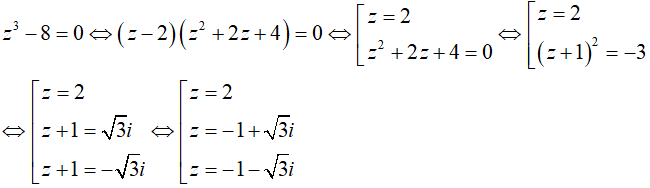
Vậy phương trình đã cho có 3 nghiệm phân biệt.
Giải phương trình số phức bậc 4
Câu 1: Phương trình \(z^4 – 6z^2 + 25 = 0\) có nghiệm là:
Lời giải
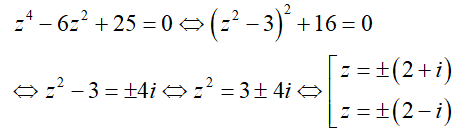
Giải phương trình số phức vi-ét
Câu 1: Biết \(z_1;z_2\) là hai nghiệm của phương trình \(z^2 + √3 z + 3 = 0\). Khi đó giá trị của \(z_1^2 + z_2^2\) là:
Lời giải

Câu 2: Gọi \(z_1;z_2\) là hai nghiệm phức của phương trình \(z^2 + 2z + 4 = 0\). Khi đó \( A = |z_1|^2 + |z_2|^2 \) có giá trị là:
Lời giải
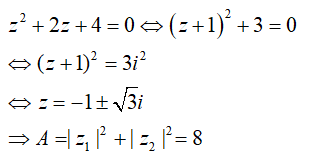
Câu 3: Cho số phức z thỏa mãn \(z^2 – 6z + 13 = 0\). Tính \(\left| x+\frac{6}{z+i} \right|\)
Lời giải
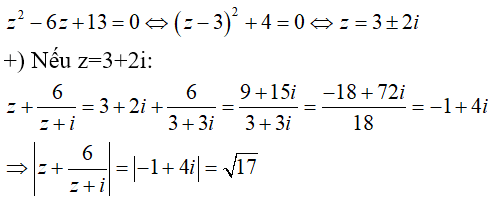
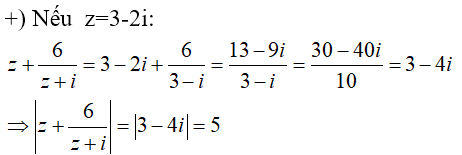
Giải phương trình số phức chứa tham số m
Câu 1: Cho phương trình \(z^2 + mz – 6i = 0.\). Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m = +(a + bi) (a,b ∈ R) có dạng . Giá trị a+2b là:
Lời giải
Gọi \(z_1;z_2\) là hai nghiệm của phương trình đã cho
Theo Viet, ta có: 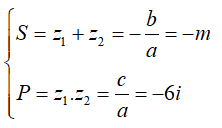
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có: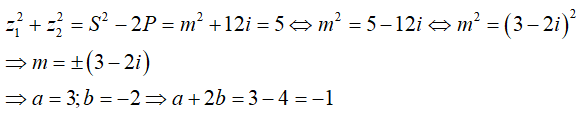
Bài tập giải phương trình bậc 2 số phức không chỉ giúp chúng ta rèn luyện kỹ năng tính toán mà còn giúp hiểu rõ hơn về sự phức tạp và đa dạng của số phức. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Bài tiếp theo: