Phương pháp Cramer là một phương pháp giải hệ phương trình tuyến tính có nhiều biến. Phương pháp này được đặt tên theo tên nhà toán học người Pháp Gabriel Cramer. Trong bài viết này, ttnguyen.net sẽ cùng các bạn tìm hiểu và làm một số bài tập giải hệ phương trình bằng phương pháp cramer nhé!
Xem thêm:
- nghiệm tầm thường và nghiệm không tầm thường
- phương trình bậc 2 số phức
I. Định lý cramer
Nếu định thức ma trận của hệ khác không thì hệ phương trình tuyến tính có một nghiệm duy nhất và ẩn số bằng tỉ số của định thức. Mẫu số là định thức của hệ, và tử số là định thức thu được từ định thức của hệ bằng cách thay thế các hệ số với ẩn số bằng các số hạng tự do. Định lý này phù hợp với một hệ phương trình tuyến tính có bậc bất kỳ.
II. Điều kiện để hệ là hệ cramer
Một hệ phương trình tuyến tính tổng quát được gọi là hệ Cramer nếu thoả mãn:
- số ẩn = số phương trình
- định thức ≠ 0
Lưu ý: Có những hệ không vuông (số phương trình ít hơn số ẩn) nhưng vẫn có thể đưa về hệ Cramer. Bằng cách, chuyển một số ẩn sang vế phải (xem là ẩn phụ) để có hệ vuông, tuy nhiên cần lưu ý khi chọn ẩn phụ để sao cho hệ mới phải là hệ Cramer (định thức của ma trận liên kết luôn khác không).
III. Công thức cramer
Hệ Cramer có nghiệm duy nhất được tính theo công thức:
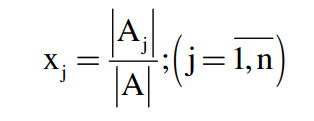
Trong đó:
- A là ma trận hệ số
- Aj là ma trận thu được từ ma trận A bằng cách thay cột thứ j bởi hệ số cột tự do
Xem thêm: bài tập ma trận có lời giải chi tiết
IV. Bài tập giải hệ phương trình cramer
Một số dạng bài tập liên quan
- giải và biện luận hệ phương trình tuyến tính theo tham số m
- Nghiệm tầm thường, không tầm thường: tìm m để hệ phương trình có nghiệm duy nhất toán cao cấp
Giải hệ bằng phương pháp cramer
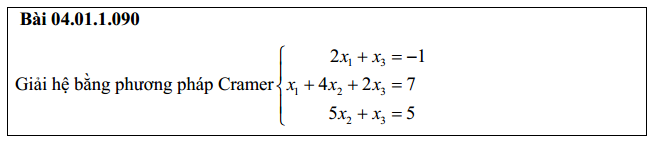
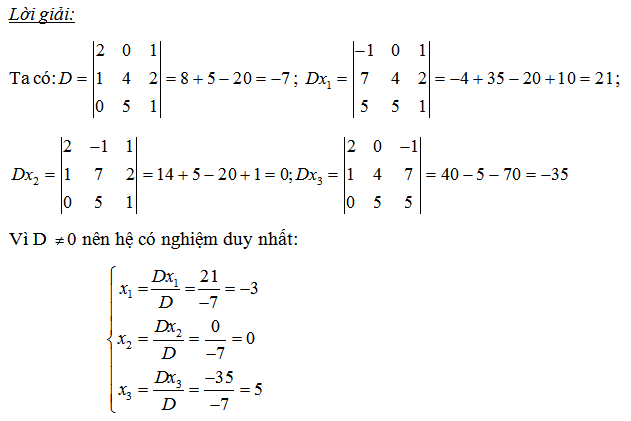
Giải hệ phương trình bằng cramer

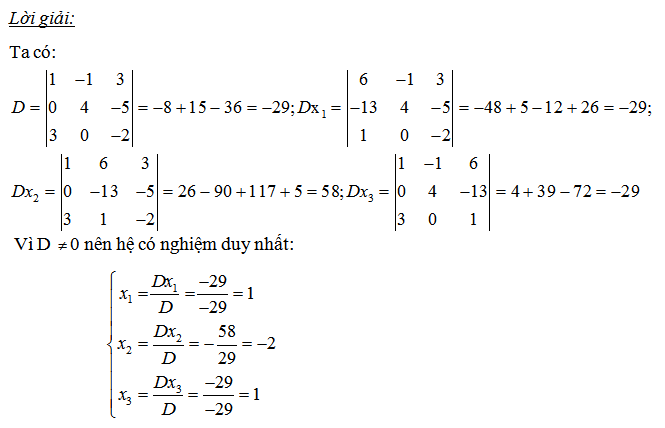
Xem thêm: hạng của ma trận
Giải hệ phương trình bằng quy tắc cramer



Giải hệ phương trình bằng phương pháp cramer



Tài liệu phương pháp hệ Cramer PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Phương pháp Cramer là một phương pháp giải hệ phương trình tuyến tính toán cao cấp khá đơn giản và dễ hiểu. Tuy nhiên, phương pháp này chỉ áp dụng được cho các hệ phương trình có số phương trình bằng số ẩn và định thức của ma trận hệ số khác 0. Cảm ơn các bạn đã theo dõi đại số và hình học giải tích trên TTnguyen.