Biểu đồ venn hay giản đồ venn là một trong những phương pháp đơn giản giúp chúng ta giải bài toán xác suất một cách dễ dàng. Dưới đây TTnguyen xin gửi tới bạn bài viết bài tập biểu đồ venn trong xác suất thống kê giúp bạn nắm rõ kiến thức về phần này.
Bài viết liên quan:
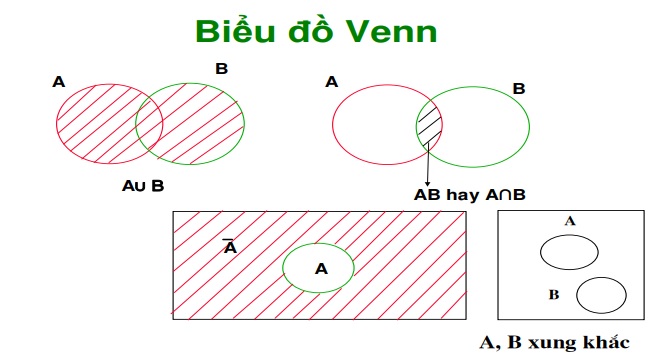
1. Biểu đồ Venn là gì?
Biểu đồ Venn hay giản đồ venn nó là một biểu đồ cho thấy được những mối quan hệ logic có thể tồn tại ở một số lượng hữu hạn của tập hợp nào đó.
2. Cách vẽ biểu đồ ven
- Sử dụng các hình tròn giao nhau để mô tả các đại lượng và mối quan hệ giữa chúng.
- Sơ đồ Ven cho ta cách nhìn trực quan quan hệ giữa các đại lượng trong bài toán và từ đó dễ dàng tìm ra các yếu tố chưa biết.
- Điền thông tin từ trong ra ngoài. từ những cái chung nhất đến cái đơn lẻ. Tức là phân tích bài toán từ cuối bài đến đầu bài toán xác suất thống kê.
Xem thêm:
- công thức xác suất đầy đủ
- không gian mẫu là gì? Ví dụ, cách xác định và ý nghĩa
- biến cố xung khắc
Bài tập về biểu đồ ven
Bài 1: Công ty sử dụng hai hình thức quảng cáo là Đài phát thanh và Vô tuyến truyền hình. Giả sử 25% khách hàng nắm được thông tin này qua vô tuyến truyền hình, 34% khách hàng nắm được thông tin qua đài phát thanh và 10% khách hàng nắm được thông tin này qua cả hai hình thức quảng cáo. Tìm xác suất để chọn ngẫu nhiên 1 khách hàng thì người đó nắm được thông tin về sản phẩm của công ty.
Giải
Gọi A là biến cố “Khách hàng nắm được thông tin về sản phẩm của công ty”
Ta vẽ sơ đồ venn:
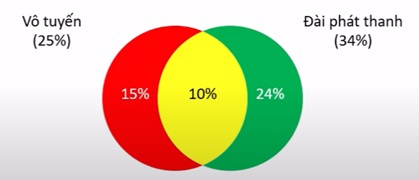
=> P(A)= 15%+10%+ 24% =49%
Biểu đồ venn xác suất thống kê
Bài 2: Một lô sản phẩm gồm 100 chiếc ấm sứ trong đó có 20 chiếc vỡ nắp, 15 chiếc sứt vòi, 10 chiếc mẻ miệng, 7 chiếc vừa vỡ nắp vừa sứt vòi, 5 chiếc vừa vỡ nắp vừa mẻ miệng, 2 chiếc vừa mẻ miệng vừa sứt vòi, 1 chiếc vừa vỡ nắp vừa vỡ vòi vừa mẻ miệng. Lấy ngẫu nhiên 1 sản phẩm để kiểm tra. Tính xác suất:
a) Sản phẩm đó có khuyết tật
b) Sản phẩm đó chỉ bị sứt vòi
c) Sản phẩm đó bị sứt vòi biết rằng nó bị vỡ nắp
Giải
Theo đầu bài, ta có sơ đồ Venn:
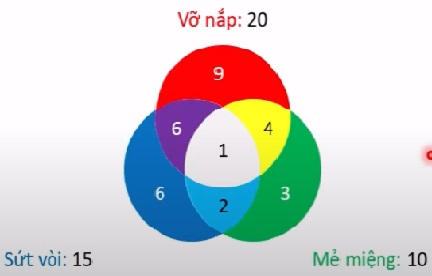
a) Gọi A là biến cố “sản phẩm bị khuyết tật”
P(A)= Số ấm có khuyết tật / số ấm có trong lô hay
\( P(A) = \frac{9+6+1+4+6+2+3}{100} = 0,31\)
b) Gọi B là biến cố “Sản phẩm chỉ bị sứt vòi”
P(B)= Số ấm chỉ sứt vòi / số ấm trong lô hay
\( P(B) = \frac{6}{100}\)
c) Gọi C là biến cố”Sản phẩm đó bị sứt vòi biết rằng nó bị vỡ nắp”
P(C)= tỉ lệ ấm sứt vòi / trong số ấm vỡ nắp
hay
\( P(C) = \frac{6+1}{20}\)
Bài toán biểu đồ ven
Bài 3: Điều tra sở thích xem TV của các cặp vợ chồng cho thấy 30% các bà vợ thường xem chương trình thể thao, 50% ông chồng thường xem chương trình thể thao, song nếu thấy vợ xem thì tỷ lệ chồng xem cũng là 60%. Lấy ngẫu nhiên một cặp vợ chồng. Tim xác suất để:
a)Cả hai người cùng thưởng xem chương trình thể thao
b)Có ít nhất một người thường xem
c) Nếu chồng xem thì vợ xem cùng
d) Nếu chồng không xem thì vợ vẫn xem
Giải
Theo đầu bài, ta có sơ đồ venn
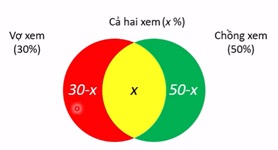
a) Vì nếu thấy vợ xem thì chồng cũng xem nên:
\( 0,6 = \frac{vợ chồng cùng xem}{vợ xem} = \frac{x}{0,3-x+x}\)
=>x= 0,18
b) Gọi B là biến cố có ít nhất một người xem:
P(B)= 12%+ 18% + 32% = 0.62
c) Gọi C là biến cố “nếu chồng xem thì vợ xem cùng”
\( P(C) = \frac{cả 2 cùng xem}{chồng xem} = \frac{18}{18+32}=0,36\)d) Gọi D là biến cố “Nếu chồng không xem thì vợ vẫn xem”
P(D)= vợ xem, chồng không xem / chồng không xem
hay
\( P(D) = \frac{12}{38+12}=0,24\)
Xem thêm:
- bài tập biến ngẫu nhiên rời rạc có lời giải
- bài tập xác suất thống kê chương 1
- bài tập biến ngẫu nhiên liên tục
Giải toán bằng sơ đồ ven
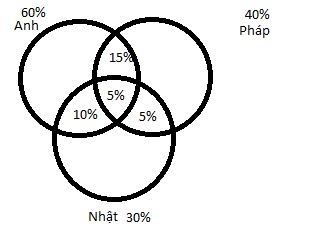
Bài 4: Một trường đại học có 60% sinh viên học tiếng Anh, 40% sinh viên học tiếng Pháp và 30% sinh viên học tiếng Nhật. Trong đó có 20% sinh viên vừa học tiếng Anh vừa học tiếng Pháp; 15% sinh viên vừa học tiếng Anh và tiếng Nhật, 10% sinh viên vừa học tiếng Pháp và tiếng Nhật; 5% sinh viên học cả 3 thứ tiếng Pháp, Anh, Nhật. Tính xác suất để chọn ngẫu nhiên một sinh viên của trường đại học đó thi:
a)Chỉ học tiếng Pháp
b)Chỉ học một trong 3 thứ tiếng
c)Chỉ học tiếng Anh và tiếng Nhật
d)Học ít nhất một trong 3 thứ tiếng
Giải
Theo đầu bài ta có sơ đồ Venn:
a)Sinh viên chỉ học tiếng Pháp là:
40%-(15%+5%+5%)=15%
Sinh viên chỉ học tiếng Anh là:
60%-(15%+5%+10%)=30%
Sinh viên chỉ học tiếng Nhật là:
30%-(10%+5%+5%)=10%
b)Vậy số sinh viên chỉ học 1 trong 3 thứ tiếng là:
15%+30%+10%=55%
c)Số sinh viên chỉ học tiếng Anh và Tiếng Nhật là:
10%(theo sơ đồ ven)
Sinh viên học 1 trong 3 thứ tiếng : 55%
Sinh viên học 2 trong 3 thứ tiếng :10%+5%+15%=30%
Sinh viên học cả 3 thứ tiếng: 5%
d)=> Số sinh viên học ít nhất 1 trong 3 thứ tiếng:
55%+30%+5%=90%
Sơ đồ venn trong xác suất thống kê
Bài 6: Một gia đình dự định sinh 3 con. Tính xác suất để sinh được:
a. Con gái đầu lòng
b. Có một trai
c. Không quá 2 trai.
Giả thiết xác suất sinh con trai và con gái bằng nhau.
Giải
Theo đầu bài ta vẽ sơ đồ cây
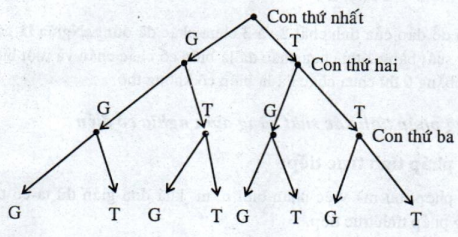
Các trường hợp có thể xảy ra đối với 1 gia đình có thể được mô tả bằng sơ đồ sau:
Theo sơ đồ trên có 8 trường hợp đồng khả năng. Đó là: GGG,GGT,GTG,GTT,TGG,TGT,TTG,TTT
a)Gọi A là biến cố”sinh con gái đầu lòng”
A={(GGG),(GGT),(GTG),(GTT)}
\( P(A) = \frac{4}{8}\)
b)Gọi B là biến cố “có một trai”
B={GGT,GTG,TGG,}
\( P(B) = \frac{3}{8}\)
c)Gọi C là biến cố”Không quá 2 trai”
C={GGG,GGT,GTG,GTT,TGG,TGT,TTG}
\( P(C) = \frac{7}{8}\)
Các dạng bài tập về biểu đồ venn
Bài 1: Nhóm có 4 bạn, trong đó có 3 bạn biết nói tiếng Anh, 2 bạn biết nói tiếng Trung. Hỏi có bao nhiêu bạn biết nói cả hai thứ tiếng?
Giải
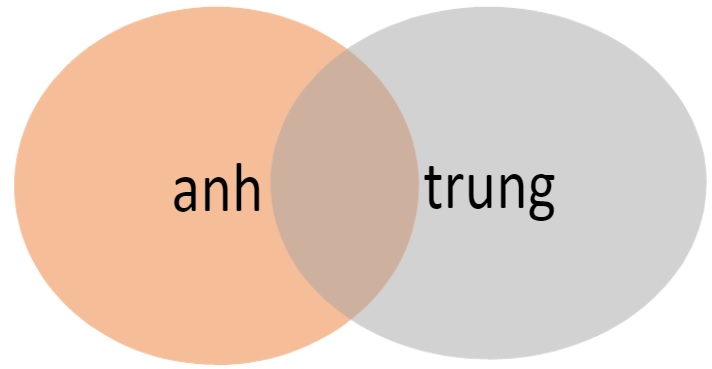
Số bạn chỉ nói được tiếng Anh là:
4 – 3 =1 (bạn)
Số bạn nói được cả 2 thứ tiếng là:
2 – 1=1 (bạn)
Đáp số: 1 bạn
Tải file tài liệu biểu đồ venn PDF miễn phí:
Xem thêm:
Trên đây là bài viết về bài tập sơ đồ venn có lời giải. Hy vọng bạn đã có đủ ví dụ và nắm vững kiến thức giải được mọi bài xác suất đại học. Chúc các bạn học tập tốt!
