Biến cố phụ thuộc, biến cố đối, biến cố xung khắc và độc lập là những khái niệm cơ bản trong lĩnh vực xác suất thống kê, được sử dụng để mô tả mối quan hệ giữa các biến cố và khả năng xảy ra của chúng. Mỗi khái niệm đều mang ý nghĩa riêng, góp phần tạo nên một hệ thống phân loại chuẩn xác và toàn diện của các biến cố trong lý thuyết xác suất. Trong bài viết này, chúng ta sẽ điểm qua và giải thích ý nghĩa của các khái niệm này.
Xem thêm:
Biến cố (Event)
Tập con E bất kỳ của không gian mẫu S gọi là biến cố.
Mỗi kết quả đơn giản gọi là biến cố đơn giản. Mỗi kết quả phức hợp gọi là biến cố phức hợp.
Biến cố độc lập là gì?
Biến cố độc lập là một biến cố mà xảy ra hoặc không xảy ra mà không bị ảnh hưởng bởi bất kỳ biến cố nào khác. Nghĩa là biến cố này không phụ thuộc vào bất kỳ biến cố nào khác xảy ra trước đó.
Ví dụ, trong việc tung một đồng xu, biến cố “mặt ngửa” và biến cố “mặt sấp” là hai biến cố độc lập với nhau. Xảy ra biến cố “mặt ngửa” không ảnh hưởng đến khả năng xảy ra biến cố “mặt sấp”, và ngược lại.
Biến cố phụ thuộc là gì?
Biến cố phụ thuộc (hay còn gọi là biến cố có điều kiện) là một biến cố xảy ra hoặc không xảy ra, tùy thuộc vào việc biến cố khác xảy ra hay không xảy ra. Nói cách khác, biến cố phụ thuộc là biến cố B phụ thuộc vào việc biến cố A xảy ra hay không xảy ra. Khi biến cố A xảy ra, biến cố B không xảy ra, còn khi biến cố A không xảy ra, biến cố B xảy ra.
Xem thêm: Bài tập xác suất có điều kiện có lời giải chi tiết
Biến cố xung khắc
Cho hai biến cố A và B bất kỳ. Nếu A ∩ B = ∅ thì ta nói rằng A và B xung khắc với nhau. Nghĩa là A và B không đồng thời xảy ra trong phép thử.
Ngược lại, nếu Nếu A ∩ B ≠ ∅ thì ta nói rằng A và B không xung khắc với nhau. Nghĩa là A và B có thể cùng xảy ra trong một phép thử.
Ví dụ : Gieo một con xúc sắc. Gọi A = {1, 2, 3}; B={2, 3, 5} .Khi đó A và B không xung khắc với nhau. C = {1, 3, 5}; D={2, 4, 6} Khi đó C và D xung khắc với nhau.
Các biến cố xung khắc từng đôi: Các biến cố A1, A2,…, An…gọi là xung khắc từng đôi nếu Ai ∩ Aj = ∅, i≠j, i, j= 1,2, ….
Biến cố giao (intersection)
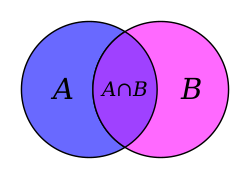
Biến cố giao của hai biến cố A và B (Ký hiệu là A ∩ B) là một biến cố bao gồm tất cả các kết quả trong cả A và B.
Nghĩa là biến cố giao A ∩ B xảy ra khi đồng thời cả hai biến cố A và B cùng xảy ra.
Xem thêm: quy tắc cộng xác suất
Biến cố hợp (Union)
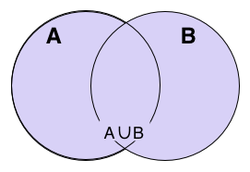
Biến cố hợp của hai biến cố là một biến cố (Ký hiệu là A ∪ B) bao gồm tất cả các kết quả của một trong hai biến cố A hoặc B .
Nghĩa là biến cố A ∪ B xảy ra nếu có ít nhất một trong hai biến cố A, B xảy ra.
Ví dụ 1: Gieo một con xúc sắc. Gọi A = {1, 2, 3}; B={2, 3, 5} . Khi đó các biến cố : A ∩ B = {2, 3}; A ∪ B = {1, 2, 3, 5}
Biến cố chắc chắn
Biến cố chắc chắn là biến cố luôn luôn sẽ xảy ra khi thực hiện một phép thử, biến cố chắc chắn thường ký hiệu là U.
Biến cố không thể có
Biến cố không thể có là biến cố không bao giờ xảy ra khi thực hiện một phép thử, biến cố không thể có thường ký hiệu là V.
Biến cố rỗng (Ký hiệu là ∅)
Biến cố không bao gồm bất cứ một kết quả nào gọi là biến cố rỗng. Nghĩa là biến cố rỗng là biến cố không bao giờ xảy ra trong phép thử.
Ví dụ 2: Gieo một con xúc sắc. Gọi A = {1, 3, 5}; B={2, 4, 6} . Khi đó các biến cố : A ∩ B = ∅
Biến cố đối (Biến cố bù – Complemet)
Biến cố đối (biến cố bù) của biến cố A, ký hiệu là Ā hoặc A’ là biến cố bao gồm các kết quả trong không gian mẫu S mà không có trong A.
Nghĩa là trong phép thử A xảy ra thì Ā không xảy ra hoặc ngược lại.
Như vậy: Ā ∩ A = ∅ và Ā ∪ A = S.
Xác suất của biến cố
Khi thực hiện một phép thử, khả năng xuất hiện của mỗi biến cố thường khác nhau. Người ta đo lường khả năng xảy ra của biến cố bởi một số, thì số đó được gọi là xác suất của biến cố.
Tiến hành phép thử ngẫu nhiên. Mỗi biến cố E của không gian mẫu S tương ứng với một số (ký hiệu là P(E)) được xác định thỏa mãn 3 tiên đề sau:
(1) 0 ≤ P(E) ≤ 1
(2) P(S) = 1
(3) Cho 2 biến cố A và B xung khắc với nhau (A ∩ B= Ø)
P(A ∪ B) = P(A) + P(B)
Khi đó số P(E) được gọi là xác suất của biến cố E.
P – Ký hiệu xác suất.
E, A, B, C – Ký hiệu các biến cố.
P (E) – Ký hiệu xác suất của biến cố E.
Hệ quả:
(1) E1, E2, …, En, … xung khắc từng đôi thì:
P(U En) = ∑ P(En), n= 1,…,∞.
(2) P(Ø) = 0
(3) Cho Ā là biến cố đối (biến cố bù) của biến cố A thì:
P(A)=1 – P(Ā) hoặc P(Ā) = 1 – P(A)
Trên đây là các loại biến cố trong xác suất thống kê. Cảm ơn bạn đã tham khảo trên ttnguyen.net.
Tải tài liệu biến cố xác suất thống kê PDF:
Bài viết liên quan:
- tổng hợp công thức thống kê
- công thức tính xác suất chi tiết đầy đủ nhất
- bài tập công thức bernoulli
- phân phối nhị thức
