Trong bài viết này, chúng ta sẽ tìm hiểu về làm một số bài tập công thức nhân xác suất có lời giải giúp các bạn hiểu rõ hơn về công thức này.
Xem thêm:
Công thức nhân xác suất
Từ công thức tính xác suất có điều kiện
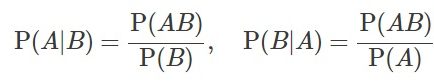
Ta suy ra công thức nhân xác suất:
|
P(A∩B) = P(A)P(B/A); Khi A xảy ra trước B. P(A∩B) = P(B)P(A/B); Khi B xảy ra trước A. |
Bài tập công thức nhân xác suất có lời giải
Bài 1: Có 20 phế phẩm trong 100 sản phẩm. Chọn ngẫu nhiên lần lượt ra 2 sản phẩm. Tính xác suất:
a. Sản phẩm thứ nhất là phế phẩm.
b. Sản phẩm thứ hai là phế phẩm khi sản phẩm thứ nhất là phế phẩm.
c. Cả hai sản phẩm lấy ra đều là phế phẩm
Giải
Gọi A1 là sản phẩm lấy ra lần thứ 1 là phế phẩm, A2 là sản phẩm lấy ra lần thứ 2 là phế phẩm
a)\(P(A)=P(A1.A2+A1 \overline{A2})\)
\(=P(A1.A2)+P(A1 \overline{A2})\)
\(=P(A1).P(A2)+P(A1).P(\overline{A2})\)
\(=\frac{C_{20}^{1}}{C_{100}^{1}}.\frac{C_{19}^{1}}{C_{99}^{1}}+\frac{C_{20}^{1}}{C_{100}^{1}}.(1-\frac{C_{19}^{1}}{C_{99}^{1}})=0,2\)
b)\(P(B)=P(A2|A1)\)
\(=\frac{P(A1A2)}{PA1}\)
\(=P(A2)=\frac{C_{19}^{1}}{C_{99}^{1}}=\frac{19}{99}\)
c)\(P(C)=P(A1.A2)=P(A1).P(A2)\)
\(=\frac{C_{20}^{1}}{C_{100}^{1}}.\frac{C_{19}^{1}}{C_{99}^{1}}=\frac{19}{495}\)
Bài tập công thức nhân xác suất
Bài 2: Có hai hộp đựng sản phẩm. Hộp thứ nhất có 7 sản phẩm loại I và 3 sản phẩm loại II; hộp thứ hai có 8 sản phẩm loại I và 4 sản phẩm loại II. Từ mỗi hộp chọn ngẫu nhiên ra một sản phẩm. Tính xác suất:
a. Lấy được 2 phẩm loại I.
b. Lấy được ít nhất một phẩm loại I.
c. Lấy được 2 sản phẩm cùng loại.
d. Nếu từ hộp thứ nhất lấy ngẫu nhiên ra 2 sản phẩm và từ hộp thứ hai lấy ngẫu nhiên ra 1 sản phẩm thì xác suất lấy được cả ba sản phẩm đều là sản phẩm loại I bằng bao nhiêu? Xác suất để 3 sản phầm cùng loại là bao nhiêu?
Giải
a) Gọi A là biến cố “Lấy được 2 sản phẩm loại I”
A1 là biến cố “lấy được 1 sản phẩm từ loại I từ hộp I”
A2 là biến cố “lấy được 1 sản phẩm từ loại I từ hộp II”
\(=> A = A1.A2 => P(A)= P(A1A2)= P(A1).P(A2)\)
\(= \frac{7}{10}. \frac{8}{12}= 0.46\)
b) Gọi B là biến cố “lấy được ít nhất một sản phẩm loại I”
\(\overline{B}\) là biến cố “lấy được 2 sản phẩm loại II”
\(\overline{B1}\) là biến cố “lấy được 1 sản phẩm từ loại II từ hộp I”
\(\overline{B2}\) là biến cố “lấy được 1 sản phẩm từ loại II từ hộp II”
=> \(P(B)= 1 – P(\overline{B}) = 1-P(\overline{B1}.\overline{B2})\)
\(= 1 -(\frac{3}{10}. \frac{4}{12})=0.9\)c) Gọi C là biến cố”lấy được 2 sản phẩm cùng loại”
\(P(C)= P(A∪\overline{B})= P(A)+P(\overline{B})\)
\(=0,46+0,9=1,36\)
d) Gọi E là biến cố “lấy 3 sản phẩm loại I”
E1 là biến cố “lấy được 2 sản phẩm từ loại I từ hộp I”
E2 là biến cố “lấy được 1 sản phẩm từ loại I từ hộp II”
\(=> E=E1.E2 => P(E)= P(E1.E2)= P(E1).P(E2)\) \(= \frac{C_{7}^{2}}{C_{10}^{2}}. \frac{C_{8}^{1}}{C_{12}^{1}}= 0,31\)Gọi F là biến cố “lấy 3 sản phẩm loại II”
F1 là biến cố “lấy được 2 sản phẩm từ loại II từ hộp I”
F2 là biến cố “lấy được 1 sản phẩm từ loại II từ hộp II”
\(=> F=F1.F2 => P(F)= P(F1.F2)= P(F1).P(F2)\) \(= \frac{C_{3}^{2}}{C_{10}^{2}}. \frac{C_{4}^{1}}{C_{12}^{1}}= .0,02\)Gọi D là biến cố “lấy 3 sản phẩm cùng loại”
P(D)=P(E∪F)=P(E)+P(F)= 0,31+0,02=0,33
Công thức nhân xác suất dùng khi nào?
Công thức nhân xác suất được sử dụng khi các biến cố độc lập với nhau và ta muốn tính xác suất của sự kiện xảy ra cùng lúc, hoặc tính xác suất của một chuỗi các sự kiện xảy ra theo một trình tự nào đó.
Trên đây là một số bài tập cơ bản và công thức nhân xác suất trong môn xác suất thống kê. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.
Tải tài liệu PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Bài viết liên quan:
Bài tập công thức bernoulli xác suất có lời giải