Dạng lượng giác của số phức là biểu diễn số phức dưới dạng A∠θ, trong đó A là trị tuyệt đối của số phức và θ là góc pha của số phức. Bằng cách sử dụng dạng lượng giác, chúng ta có thể dễ dàng thực hiện các phép toán như cộng, trừ, nhân và chia trên số phức.
Sau đây, hãy cùng ttnguyen.net tìm hiểu khái niệm dạng lượng giác của số phức và các bài tập liên quan nhé!
Bài viết liên quan:
1. Khái niệm dạng lượng giác của số phức
Dạng lượng giác của số phức được biểu diễn bằng công thức có dạng: \(z=r(cos\varphi + isin\varphi)\).
Trong đó:
- z là số phức.
- r là độ lớn (hoặc module) của số phức.
- φ là acgumen của số phức.
2. Các phép toán với số phức lượng giác
Các phép toán cơ bản trên số phức lượng giác bao gồm cộng, trừ, nhân và chia. Dưới đây là các công thức phép toán cho số phức dạng lượng giác:
Cho hai số phức \(z_1 = r_1(\cos \varphi_1 + i\sin \varphi_1)\) và \(z_2 = r_2(\cos \varphi_2 + i\sin \varphi_2)\), trong đó \(r_1\), \(r_2\) là độ lớn và \(\varphi_1\), \(\varphi_2\) là acgumencủa số phức tương ứng:
– Phép cộng: \( z_1 + z_2 = (r_1 \cos \varphi_1 + r_2 \cos \varphi_2) + i(r_1 \sin \varphi_1 + r_2 \sin \varphi_2) \)
– Phép trừ: \(z_1 – z_2 = (r_1 \cos \varphi_1 – r_2 \cos \varphi_2) + i(r_1 \sin \varphi_1 – r_2 \sin \varphi_2)\)
– Phép nhân: \( z_1 \cdot z_2 = r_1 r_2 (\cos (\varphi_1 + \varphi_2) + i\sin (\varphi_1 + \varphi_2)) \)
– Phép chia: \( \frac{z_1}{z_2} = \frac{r_1}{r_2} (\cos (\varphi_1 – \varphi_2) + i\sin (\varphi_1 – \varphi_2)) \)
3. Công thức Moivre
Công thức Moivre được sử dụng để tính các lũy thừa của số phức dạng lượng giác. Cho số phức \(z = r(\cos \varphi + i\sin \varphi)\), công thức có dạng:
\(z^n = [r(\cos \varphi + i\sin \varphi)]^n = r^n(\cos(n\varphi) + i\sin(n\varphi))\)Tuyển tập các bài tập về số phức liên hợp của số phức
4. Chuyển số phức sang dạng lượng giác
Để chuyển số phức sang dạng lượng giác, chúng ta có thể làm theo các bước sau:
Bước 1: Tìm r: đó là module của z, \(r=\sqrt{a^2+b^2}\), trong đó a và b lần lượt là phần thực và phần ảo của số phức.
Bước 2: Tìm φ: đó là acgumen của z; φ là một số thực sao cho cos φ = ar và sin φ = br;
Bước 3: Biểu diễn số phức dưới dạng: \(z = r(\cos \varphi + i\sin \varphi)\)
Đổi số phức sang dạng lượng giác casio: tại đây
Bài tập chuyển số phức sang dạng lượng giác
Ví dụ 1: Biến đổi các số phức sau sang dạng lượng giác:
a.\( z_1=6+6i\)
b.\( z_1=\frac{-1}{4}+\frac{\sqrt{3}}{4}i\)
c. \(z_1=\frac{5\sqrt{3}}{4}+\frac{5}{2}i\)
Lời giải
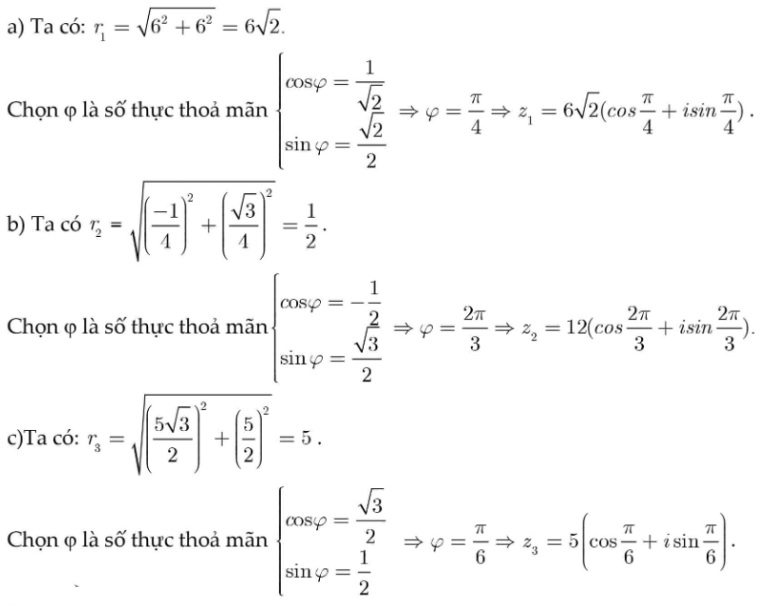
Tổng hợp toàn bộ công thức số phức toán cao cấp
Ví dụ 2: Lượng giác hoá số phức:
a, 5
b, -7
c, 6i
d, -10i
Lời giải
a, \(5 = 5(1+0i) = 5(cos0+i sin0)\)
b, \(-7 = 7(-1+0i) = 7(cos\pi+sin\pi i)\)
c, \(6i=6(0+i)=6(cos\frac{\pi }{2}+isin\frac{\pi }{2})\)
d, \(-10i=10(0-i)=10(cos-\frac{\pi }{2}+isin-\frac{\pi }{2})\)
Tìm dạng lượng giác của số phức toán cao cấp
Ví dụ 1: Biến đổi số phức sau dưới dạng lượng giác:
\(z=(1-i\sqrt{3}).(1+i)\)Lời giải
Có:
\((1-i\sqrt{3})=2.[cos(-\frac{\pi}{3})+isin(-\frac{\pi}{3})]\) \((1+i)=\sqrt{2}[cos\frac{\pi}{4}+isin\frac{\pi}{4}]\)Áp dụng công thức nhân số phức dạng lượng giác ta có:
\(z=(1-i\sqrt{3}).(1+i)=\) \( 2\sqrt{2}[cos(-\frac{\pi}{2})+isin(-\frac{\pi}{2})]\)Ví dụ 2: Đưa số phức về dạng lượng giác:
\(z=\frac{1-i}{(1-i\sqrt{3}).(2+2i)}\)Lời giải
\((1-i\sqrt{3})=2(cos\frac{\pi}{6}+isin\frac{\pi}{6})\) \((2+2i)=2\sqrt{2}(cos\frac{\pi}{4}+isin\frac{\pi}{4})\)=>\((1-i\sqrt{3})(2+2i)=4\sqrt{2}(cos\frac{5\pi}{12}+isin\frac{5\pi}{12})\)
Mà: \(1-i=\sqrt{2}[cos(-\frac{\pi}{4})+isin(-\frac{\pi}{4})]\)
Vậy: \(z=\frac{1-i}{(1-i\sqrt{3}).(2+2i)}=\frac{\sqrt{2}}{4\sqrt{2}}.[cos(-\frac{\pi}{4}-\frac{5\pi}{12})+isin(-\frac{\pi}{4}-\frac{5\pi}{12})]\)
\(\frac{1}{4}.[cos(-\frac{2\pi}{3})+isin(-\frac{2\pi}{3})]\)Ví dụ 3: Viết số phức dưới dạng lượng giác:
a, \((1+3i)(i+2i)\)
b, \((1+i)\left [ 1+(\sqrt{3}-2) i\right ]\)
c, \((\sqrt{2}-2i)\left [ \sqrt{2} +(3\sqrt{2}-4)i\right ]\)
Lời giải
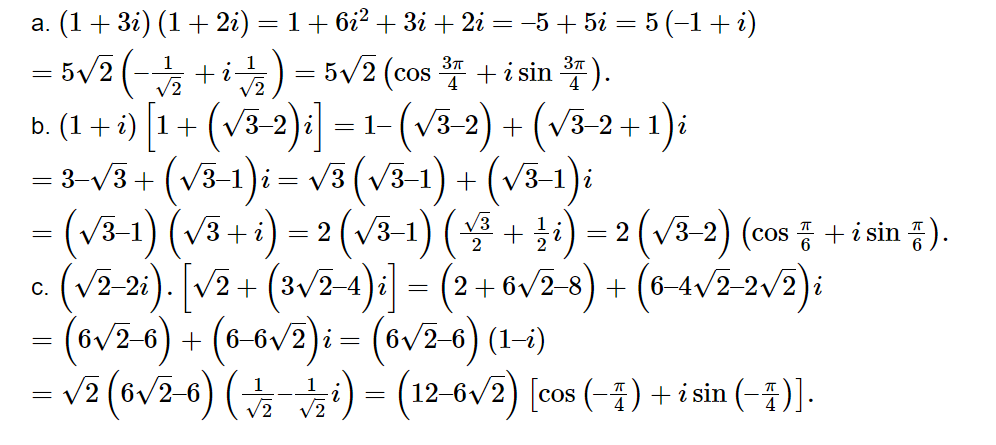
Ví dụ 4: Biến đổi các số phức sang dạng lượng giác:
a, \(1+\frac{i}{\sqrt{3}}\)
b, \(1+\sqrt{3}+(1-\sqrt{3})i\)
Lời giải

Ví dụ 5: Viết dạng lượng giác của số phức:
a, \(\frac{1}{2+2i}\)
b, \(\frac{3-i}{1-2i}\)
c, \(\frac{1-i\sqrt{3}}{1+i}\)
Lời giải

Bài tập công thức Moivre
Ví dụ 1: Biểu diễn số phức dưới dạng lượng giác
a.\((\sqrt{2}+\sqrt{2}i)^{10}\)
Lời giải
\(\sqrt{2}+\sqrt{2}i=2.(cos(\frac{\pi}{4})+isin(\frac{\pi}{4}))\)Do đó: \((\sqrt{2}+\sqrt{2}i)^{10}=[2.(cos(\frac{\pi}{4})+isin(\frac{\pi}{4}))]^{10}\)
\(=2^{10}.[cos(\frac{10\pi}{4})+isin(\frac{10\pi}{4})]\) \(=2^{10}.[cos(\frac{5\pi}{2})+isin(\frac{5\pi}{2})]\)
b. \(\frac{(1-i)^{10}}{(\sqrt{3}+i)^{9}}\)
Lời giải

Ví dụ 2: Giải số phức bằng dạng lượng giác: \(z =1-cos\frac{\pi }{8}+i.sin\frac{\pi }{8}\). Tính \(z^{1012}\)
Lời giải

Ví dụ 3: Cho số phức: \(z=1+i\sqrt{3}\). Tính \(z^{2020}\)
Lời giải
\(z=1+\sqrt{3}=2(\frac{1}{2}+i\frac{\sqrt{3}}{2})=2(cos\frac{\pi}{3}-isin\frac{\pi}{3})\) \(z^{2020}=2^{2020}[cos(2020.\frac{\pi}{3})+isin(2020.\frac{\pi}{3})]\) \(2^{2020}[-\frac{1}{2}-i\frac{\sqrt{3}}{2}]=-2^{2019}-2^{2019}-i\sqrt{3}\)Công thức khai triển lũy thừa bậc 3
\((cos\varphi +isin\varphi )^{3}=cos^{3}\varphi -3cos\varphi sin^{2}\varphi +i(3cos^{2}\varphi sin\varphi -sin^{3}\varphi )\)Mặt khác theo công thức Moivre:
\((cos\varphi +isin\varphi )^{3}=cos3\varphi =isin3\varphi\)Từ đó suy ra:
\(cos3\varphi =cos^{3}\varphi -3cos\varphi sin^{2}\varphi =4cos^{3}\varphi -3cos\varphi \) \(sin3\varphi =3cos^{2}\varphi sin\varphi -sin^{3}\varphi =3sin\varphi -4sin^{3}\varphi \)Tương tự, bằng cách đối chiếu công thức khai triển lũy thừa bậc n của nhị thức cosφ+i sinφ với công thức Moivre, ta có thể biểu diễn cos nφ và sin nφ theo các lũy thừa của cosφ và sinφ.
Căn bậc hai của số phức dạng lượng giác
Từ công thức Moivre, dễ thấy số phức z=r(cosφ+isinφ),r>0 có 2 căn bậc hai là:
\(\sqrt{r}(cos\frac{\varphi }{2}+isin\frac{\varphi }{2})$ và $-\sqrt{r}(cos\frac{\varphi }{2}+isin\frac{\varphi }{2})=\sqrt{r}(cos(\frac{\varphi }{2}+\pi )+isin(\frac{\varphi }{2}+\pi ))\)Ví dụ 1: Căn bậc hai của số phức 4 + 65i là:
Lời giải:
Giả sử v là một căn bậc hai của \(4+6\sqrt{5}i\). Ta có:
\(v^{2}=4+6\sqrt{5}i\Leftrightarrow w^{2}=(3+\sqrt{5}i)^{2}\Leftrightarrow w=\pm (3+\sqrt{5})i\)Trên đây là lý thuyết kèm một số bài tập vận dụng chuyển số phức về dạng lượng giác toán cao cấp trong môn đại số tuyến tính. Cảm ơn ae.
Bài viết liên quan: