Bài viết dưới đây, TTnguyen sẽ tổng hợp lại kiến thức về quy tắc cộng xác suất và một số phương pháp giải giúp các bạn ôn tập dễ dàng. Bắt đầu thôi!!!
Xem thêm:
- Tổng hợp công thức tính xác suất chi tiết và đầy đủ nhất
- Bài tập công thức xác suất đầy đủ
- công thức nhân xác suất
I. Công thức cộng xác suất
Xét một phép thử, ta có công thức cộng xác suất như sau:
– Nếu A, B là hai biến cố tuỳ ý thì:
| P(A + B) = P(A) + P(B) – P(AB) |
– Nếu A, B là hai biến cố xung khắc thì:
| P(A + B) = P(A) + P(B) |
– Mở rộng:
| P(A + B + C) = P(A) + P(B).P(C) – P(AB) – P(BC) – P(AC) |
+ Biến cố hợp: Cho hai biến cố A và B. Biến cố “ A hoặc B xảy ra”, kí hiệu là A∪B, được gọi là hợp của hai biến cố A và B.
+ Biến cố xung khắc: Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.
II. Bài tập quy tắc cộng xác xuất có lời giải
Bài 1: Rút một lá bài từ bộ bài 52 lá. Gọi A là biến cố lấy được lá màu đen. B là biến cố rút được lá màu đỏ.
– Hỏi A, B có xung khắc không?
– Tính P(A + B)
Giải
A, B có xung khắc.
P(A + B) = P(A) + P(B) = 26/52 + 26/52 =1
Bài 2: Gieo một con súc sắc đồng chất. Tính xác suất để xuất hiện mặt 1 chấm hoặc 6 chấm?
Giải
Gọi A là biến cố con súc sắc xuất hiện mặt 1 chấm.
B là biến cố con súc sắc xuất hiện mặt 6 chấm.
⇒ A ∪ B: Con súc sắc xuất hiện mặt 1 chấm hoặc 6 chấm.
Ta có: P(A)= 1/6;P(B)= 1/6
⇒ P (A ∪ B)=P(A)+P(B)= 1/6 + 1/6 = 1/3
III. Quy tắc cộng xác suất của hợp 2 biến cố
Bài 3: Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên hai viên bi. Xác suất để chọn được hai viên bi cùng màu là?
Giải
Gọi A là biến cố : “Chọn được hai viên bi xanh”.
Gọi B là biến cố : “Chọn được hai viên bi đỏ”.
Gọi C là biến cố : “Chọn được hai viên bi vàng”.
Khi đó biến cố: “Chọn được hai viên bi cùng màu” là biến cố A∪B∪C. Do A; B; C đôi một xung khắc với nhau nên theo quy tắc cộng ta có
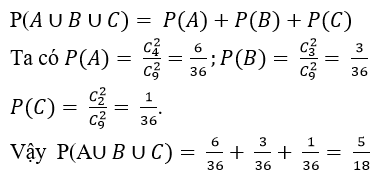
Bài 4: Trong kì thi học sinh giỏi có 10 học sinh đạt giải trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng . Tính xác suất để chọn được một nhóm gồm 5 học sinh mà có cả nam và nữ, biết số học sinh nam ít hơn số học sinh nữ
Giải
+ Không gian mẫu: \(n(\Omega) = C^{5}_{10}=252\)
+ Gọi A là biến cố chọn được 4 nữ và 1 nam.
+ Gọi B là biến cố chọn được 3 nữ và 2 nam.
+ Ta tính số kết quả thuận lợi cho hai biến cố A và B :
\(n(A) = C^{4}_{6}.C^{1}_{4}=60; n(B) = C^{3}_{6}.C^{2}_{4}=120\)Hai biến cố A và B xung khắc với nhau; áp dụng quy tắc cộng xác suất ta có:
P(A∪B) = P(A) + P(B) = 60/252 + 120/252 = 5/7
Trên đây là lý thuyết và một số bài tập vận dụng công thức cộng môn xác suất thống kê kèm theo lời giải chi tiết. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.
Tài liệu quy tắc cộng xác suất PDF:
Bài viết liên quan:
- biểu đồ venn trong xác suất thống kê
- xác suất có điều kiện
- công thức bernoulli
- bài tập xác suất thống kê chương 1 có lời giải
