Trong bài viết này, chúng mình sẽ tìm hiểu về phép thế và dấu của phép thế: khái niệm, ví dụ, cách biểu diễn và một số bài tập phép thế.
Xem thêm:
- bài tập ma trận có lời giải
- nhân 2 ma trận – Điều kiện và cách tính có lời giải
- ánh xạ tuyến tính – bài tập và lời giải
- dạng song tuyến tính – bài tập và lời giải
Định nghĩa
Cho n là một số tự nhiên khác 0. Một song ánh σ từ tập \(I_n = {1,2,…,n}\) đến chính nó được gọi là một phép thế bậc n. Phép thế σ bậc n được biểu diễn dưới dạng bảng dòng như sau:
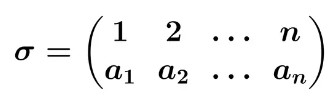
\(S_n\) là tập hợp các phép thế bậc n.
Phép thế cấp n được gọi là hoán vị. Do đó, tập \(S_n\) có n! phần tử.
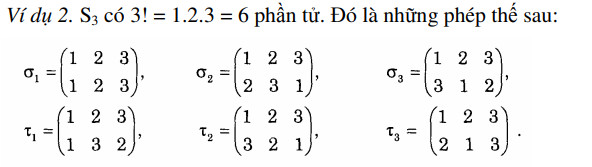
Ví dụ phép thế

Phép toán trên các phép thế
Tích hai phép thế
Cho σ và τ là hai phép thế bậc n. Khi đó hợp thành của hai song ánh σ và τ (ký hiệu σ Ο τ ) cũng là một phép thế bậc n và được gọi là tích của hai phép thế σ và τ:
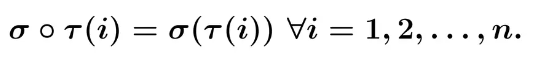
Ánh xạ ngược của σ ký hiệu \(σ^{-1}\) cũng là một phép thế bậc n, được gọi là một nghịch đảo của σ.
Chú ý:
- Do phép hợp thành các ánh xạ (tích các phép thế) có tính chất kết hợp nên bằng quy nạp người ta có thể mở rộng định nghĩa cho tích của nhiều phép thế. Đặc biệt, ta có định nghĩa: \(σ^{n} = σ^{n-1} Ο τ \).
- Do phép hợp nên các song ánh không có tính chất giao hoán nên các tích các phép thế cũng không có tính chất giao hoán.
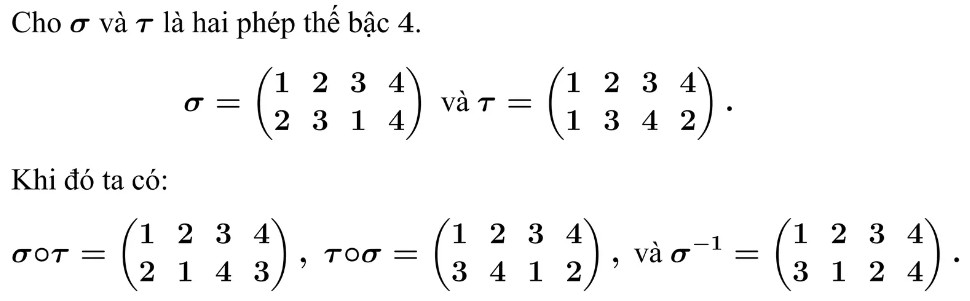
Xích
Xét một phép thế cấp n đặc biệt. cho k số tự nhiên phân biệt \(i_1, i_2,…, i_k\) ∈ {1,2,…,n}.
Xét phép thế σ được xác định như sau:
\(σ(i_1), σ(i_2) = i_3,..,σ(i_{k-1}) = i_k, σ(i_k) = i_1\) và σ(j) = j với mọi j ∈ {1,2,…,n} \ \({i_1, i_2,…, i_k}\). Khi đó, σ được gọi là một xích có độ dài k.
Ký hiệu xích: σ = \((i_1, i_2,…, i_k)\).
Tập hợp \({i_1, i_2,…, i_k}\) được gọi là nên của xích \((i_1, i_2,…, i_k)\). Hai xích được gọi là rời nhau nếu tập nền của chúng rời nhau (tức có giao bằng rỗng).
Nếu k = 2 thì σ được gọi là chuyển trí và thường vết \((i_k, i_l)\).
Biểu diễn của phép thế
Mỗi phép thế cấp n đều là tích của các xích rời nhau.
Mỗi xích là tích các phép thế chuyển trí.
Mỗi phép thế đều là tích của các phép thế chuyển trí.

Nghịch thế
Cho σ là một phép thế bậc n. Nếu với 1 ≤ i < j ≤ n mà ta có σ(i) > σ(j) thì ta gọi cặp (σ(i) , σ(j)) là một nghịch thế của σ.


Cấp của phép thế
Cấp của phép thế bằng bội chung nhỏ nhất của độ dài các xích rời rạc.
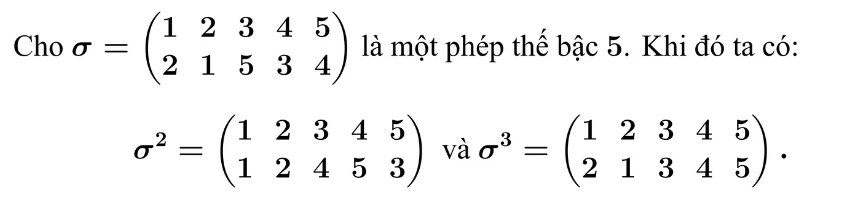
Dấu của phép thế
Dấu của phép thế σ , ký hiệu s(σ) và được tính bởi công thức \(s(σ) = (-1)^{N(σ)}\). Trong đó: N(σ) là số các nghịch thế của σ.
Độ dài của một phép thế chẵn nếu độ dài của xích lẻ => Phép thế được gọi là phép thế chẵn nếu dấu của nó bằng 1.
Độ dài của một phép thế lẻ nếu độ dài của xích chẵn => Phép thế được gọi là phép thế lẻ nếu dấu của nó bằng -1
Mệnh đề
- Mệnh đề 1: Cho σ và τ là hai phép thế bậc n: s(σ Ο τ) = s(σ).s(τ).
- Mệnh đề 2: Cho σ là một phép thế và t ∈ N thì: \(s(σ^{t}) = s(σ)^{t}\), \(s(σ^{-1})= s(σ)\).
- Nếu n > 1 thì trong số n! phép thế bậc n, có n!/2 phép thế chẵn và n!/2 phép thế lẻ.
Bài tập phép thế
Bài 1: Thực hiện các phép nhân sau đây, viết các phép thế thu được thành tích các xích rời nhau và tính dấu của chúng. Xác định thêm ánh xạ ngược của các phép thế thu được.
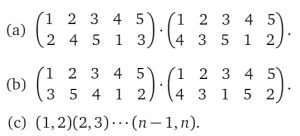
Giải

Bài 2: Cho phép thế σ ∈ Sn.Đặt τ(i) = σ(n+1−i) với 1≤i≤n.Khi đó τ cũng là một phép thế cấp n.Giả sử số nghịch thế của σ là k thì số nghịch thế của τbằng bao nhiêu?
Giải

Bài 3: Với mỗi phép thế sau hãy xác định dấu của nó, tìm phép thế nghịch đảo và dấu của phép thế nghịch đảo:

Giải
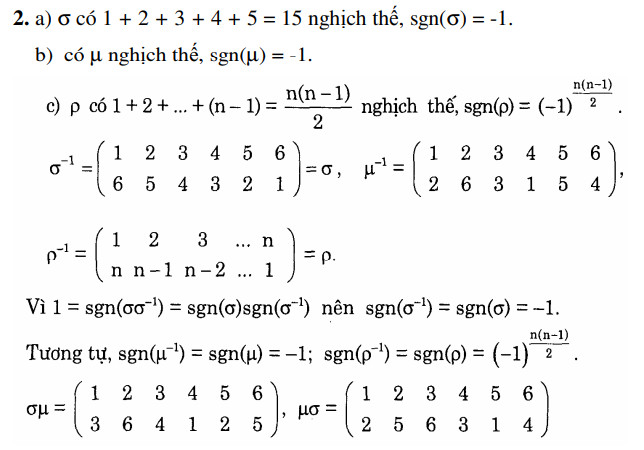
Trên đây là kiến thức cơ bản và một số bài tập phép thế kèm lời giải chi tiết giúp bạn ôn tập dễ dàng. Cảm ơn bạn đã tham khảo đại số tuyến tính trên ttnguyen.net.
Tài liệu phép thế và dấu của phép thế PDF:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Bài viết liên quan:
- Tóm tắt công thức đại số tuyến tính – Ngắn gọn dễ học nhất
- Trắc nghiệm đại số tuyến tính có đáp án 80 câu hutech
- Giáo trình đại số tuyến tính PDF – Nguyễn Hữu Việt Hưng
- Top 5 App/Web giải đại số tuyến tính giúp bạn đạt điểm cao