Căn bậc hai của một số phức là cặp số phức, bình phương của chúng là số phức gốc ban đầu. Chúng có thể được xác định tương tự như căn bậc hai của một số tự nhiên.
Trong bài viết này, chúng ta sẽ tìm hiểu về khái niệm của căn bậc 2 của số phức và một số bài tập liên quan cùng phương pháp giải. Bắt đầu thôi!
Bài viết liên quan:
Căn bậc 2 của số phức là gì?
Căn bậc hai của số phức là một số phức khác, bình phương của nó chính là số phức đã cho.
Ví dụ, nếu căn bậc hai của số phức \(a + ib\) là \(\sqrt{(a + bi)} = x + yi\), thì chúng ta có \((x + yi)^{2} = a + bi\).
Cách tìm căn bậc 2 của số phức
Trường hợp w là số thực: Nếu a là một số thực:
- a < 0 ; a có các căn bậc hai là \(\pm i\sqrt{|a|}\)
- a = 0, a có đúng một căn bậc hai là 0.
- a > 0, a có hai căn bậc hai là \(\pm\sqrt{a}\)
Trường hợp w = a + bi; a, b ∈ R; b ≠ 0
Gọi z = x + yi là một căn bậc hai của w khi và chỉ khi \(z^2 =w\), tức là
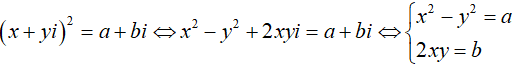
Mỗi cặp số thực (x; y) nghiệm đúng hệ phương trình trên cho ta một căn bậc hai x + y.i của số phức w = a + bi.
Xem thêm: Tổng hợp công thức số phức full không “che”
Tìm căn bậc 2 của số phức bằng máy tính
Để tính căn bậc 2 của số phức bằng máy tính bạn có thể làm theo các bước sau:
Trong môi trường số phức (MODE 2) ta bấm như hình dưới. Giải thích: Phần bên trái là căn mô đun của 3+4i, phần bên phải là 1 nửa Argument của 3+4i.

Bài tập tìm căn bậc 2 của số phức có lời giải
Ví dụ 1: Tìm các căn bậc hai của w = -5 + 12i.
Lời giải
Gọi z = x + yi là một căn bậc hai của số phức w = -5 + 12i
Ta có z2 = w <=> (x + yi)2 = -5 + 12i
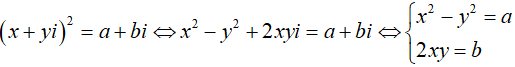
Vậy số phức w có hai căn bậc hai là 2 + 3i và -2 – 3i.
Ví dụ 2: Khai căn bậc hai số phức z = -3 + 4i có kết quả:
Lời giải
Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
w2 = z <=> (x + yi)2 = -3 + 4i
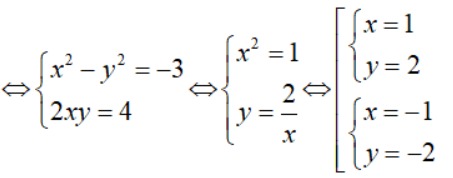
Do đó z có hai căn bậc hai là:
- z1 = 1 + 2i
- z2 = -1 – 2i
Liên quan:
Ví dụ 3:Tính căn bậc hai của số phức z = 8 + 6i
Lời giải
Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.
Ta có:

Do đó z có hai căn bậc hai là
- z1 = 3 + i
- z2 = -3 – i
Ví dụ 4: Cho z = 3 + 4i. Tìm căn bậc hai của z.
Lời giải
Giả sử w = x + yi là một căn bậc hai của số phức z = 3 + 4i.
Ta có:
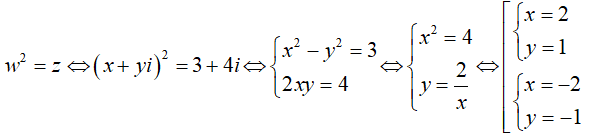
Do đó z có hai căn bậc hai là
- z1 = 2 + i
- z2 = -2 – i
Ví dụ 5: Căn bậc hai của số phức 4 + 6√5i là:
Lời giải
Giả sử w là một căn bậc hai của 4 + 6√5i. Ta có:
![]()
Ví dụ 6:Gọi z là căn bậc hai có phần ảo âm của 33 – 56i. Phần thực của z là:
Lời giải
Ta có: 33 – 56i = (7 – 4i)2 => z = 7 – 4i
Do đó phần thực của z là 7.
Ví dụ 7:Tìm căn bậc hai của -121 là:
Lời giải
Ta có: z = -121 nên z = (11i)2 .
Do đó z có hai căn bậc hai là z = 11i và z = -11i
Kết luận
Trong đại số tuyến tính, căn bậc hai của số phức là một khái niệm quan trọng. Nó cho phép chúng ta tìm ra một số phức khác, khi bình phương của nó sẽ cho kết quả giống với số phức ban đầu. Tính toán căn bậc hai của số phức có thể được thực hiện bằng cách sử dụng các công thức và phương pháp tương ứng. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.
Xem thêm: