Nguyên lý Dirichlet, hay còn gọi là nguyên lý chuồng bồ câu giúp giải quyết nhiều bài toán tổ hợp và chứng minh các định lý. Nguyên lý này được nhà toán học người Đức Peter Gustav Lejeune Dirichlet đề xuất vào thế kỷ 19. Bài viết sau đây sẽ giới thiệu lý thuyết và một số bài tập nguyên lý dirichlet toán rời rạc có lời giải..
Xem thêm:
bài tập toán rời rạc chương 1 có lời giải
I. Định lý Dirichle
1. Định nghĩa cơ bản
Giả sử k là một số nguyên dương, nếu cho k + 1 (nhiều hơn) đồ vật được đặt vào trong k hộp, thì có ít nhất một hộp chứa hai đồ vật. Nói cách khác, nếu đem xếp nhiều hơn n đối tượng vào n hộp thì luôn tìm được một cái hộp chứa không ít hơn 2 đối tượng.
Nguyên lý này được phát triển từ một mệnh đề rất đơn giản gọi là nguyên lý “nguyên lý quả cam” hay là nguyên lý “chuồng chim bồ câu”.
Ví dụ: Nếu có 11 quả cam được đặt vào 10 giỏ, thì ít nhất một giỏ chứa hai quả cam.
2. Nguyên lý Dirichlet cơ bản
Nếu nhốt n+1 con chim bồ câu vào n cái chuồng thì bao giờ cũng có một chuồng chứa ít nhất 2 con chim bồ câu.
3. Nguyên lý Dirichle tổng quát
Nếu đem xếp n đối tượng vào k hộp thì luôn tìm được một hộp chứa ít nhất [n/k] đối tượng.
4. Nguyên lý Dirichlet dạng tập hợp
Cho A và B là hai tập hợp khác rỗng có số phần tử hữu hạn, mà số lượng phần tử của A lớn hơn số lượng phần tử của B. Nếu với một quy tắc nào đó, mỗi phần tử của A cho tương ứng với một phần tử của B, thì tồn tại ít nhất hai phần tử khác nhau của A mà chúng tương ứng với một phần tử của B.
Hay nói cách khác:
Nếu |A| > |B| và mỗi phần tử của A được ánh xạ đén một phần tử của B thì tồn tại ít nhất 2 phẩn tử A ánh xạ đến cùng một phần tử của B.
5. Nguyên lý Dirichlet mở rộng
Nếu nhốt n+1 con chim bồ câu vào m ≥ 2 cái chuồng thì tồn tại một chuồng có ít nhất \(\left[ \frac{n+m+1}{m} \right]\) con chim bồ câu.
6. Nguyên lý Dirichlet dạng tập hợp mở rộng
Giả sử A, B là hai tập hợp hữu hạn và S(A), S(B) tương ứng kí hiệu là các số lượng phần tử của A và B. Giả sử có một số tự nhiên k nào đó mà S(A) > k.S(B) và ta có quy tắc cho tương ứng mỗi phần tử của A với một phần tử của B. Khi đó tồn tại ít nhất k+1 phần tử của A mà chúng tương ứng với cùng một phần tử của B.
Ví dụ 1: Cần bao nhiêu người để khi chọn một cách tùy ý thì có ít nhất hai người có cùng ngày sinh nhật?
Lời giải
Bởi chỉ có đúng 366 ngày sinh nhật có thể.
→ cần có 367 người thì sẽ có ít nhất hai người có cùng ngày sinh nhật.
Ví dụ 2: Cần có bao nhiêu chữ cái tiếng Anh để khi chọn một cách tùy ý có ít nhất hai chữ cái giống nhau?
Lời giải
27 chữ cái tiếng Anh, phải có ít nhất hai chữ cái giống nhau.
Ví dụ 3: Cần phải có bao nhiêu sinh viên trong một lớp học để đảm bảo rằng có ít nhất hai sinh viên nhận được kết quả đánh giá học phần giống nhau, nếu điểm được cho từ 0 đến 100?
Giải
Bởi có 101 kết quả khả thi.
Theo nguyên lý Dirichle:
Bất kỳ nhóm 102 sinh viên nào cũng sẽ có ít nhất hai sinh viên có cùng kết quả.
Xem thêm: chỉnh hợp lặp
II. Ví dụ về nguyên lý Dirichlet
Ví dụ 1: Trong 100 người tuỳ ý, có thể khẳng định có bao nhiều người có cùng tháng sinh nhật?
Lời giải
Trong 100 người có ít nhất [100/12] = [8.33] = 9 người có cùng tháng sinh.
Ví dụ 2: Cần tối thiểu bao nhiêu sinh viên trong lớp học để đảm bảo rằng có ít nhất sáu sinh viên nhận cùng kết quả đánh giá nếu có năm điểm chữ dùng để đánh giá A, B, C, D, F?
Lời giải
Số sinh viên tối thiểu cần để đảm bảo rằng có ít nhất sáu sinh viên nhân cùng điểm đánh giá là số nguyên nhỏ nhất N sao cho [N/5]=6.
=> N = 5.5+1=26
=> có ít nhất 2 điểm có trung điểm là tọa độ nguyên.
Ví dụ 3: Cho 9 điểm có toạ độ nguyên trong không gian 3 chiều. Chứng minh rằng có ít nhất 2 điểm mà trung điểm của chúng có cùng toạ độ nguyên
Giải
Giả sử trong mặt phẳng Oxyz có A(x1,y1,z1), B(x2,y2,z2). Vậy trung điểm của đoạn thẳng AB sẽ là:
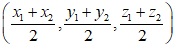
Các tọa độ này nguyên khi: các tọa độ này có cùng tính chẵn lẻ
Chia các số thành các nhóm
Nhóm 1: (chẵn, chẵn, chẵn)
Nhóm 2: (chẵn, lẻ, chẵn)
Nhóm 3: (chẵn, chẵn, lẻ)
Nhóm 4: (chẵn, lẻ, lẻ)
Nhóm 5: (lẻ, lẻ, lẻ)
Nhóm 6: (lẻ, chẵn, lẻ)
Nhóm 7: (lẻ, chẵn, chẵn)
Nhóm 8: (lẻ, lẻ, chẵn)
Vì có 8 nhóm có tính chẵn lẻ với nhau. Nên theo nguyên lý Dirichlet có ít nhất 2 điểm thuộc cùng 1 nhóm có tính chẵn lẻ như nhau. Do đó trung điểm của 2 điểm đó sẽ có tọa độ nguyên (đpcm)
Giả sử lấy ngẫu nhiên 9 điểm trong không gian Oxyz:
(2;4;6) , (2,4,5) , (1,3,6) , (7,8,9) , (2,5,1) , (1,2,6) , (6,4,9) , (4,6,7) , (3,5,8)
Chia thành 8 nhóm như trên ta được:
Nhóm 1: (chẵn, chẵn, chẵn) (2;4;6)
Nhóm 2: (chẵn, lẻ, chẵn)
Nhóm 3: (chẵn, chẵn, lẻ) (2,4,5) (6,4,9) (4,6,7)
Nhóm 4: (chẵn, lẻ, lẻ) (2,5,1)
Nhóm 5: (lẻ, lẻ, lẻ)
Nhóm 6: (lẻ, chẵn, lẻ) (7,8,9)
Nhóm 7: (lẻ, chẵn, chẵn) (1,2,6)
Nhóm 8: (lẻ, lẻ, chẵn) (1,3,6) (3,5,8)
III. Bài tập về nguyên lý dirichlet có lời giải
Bài 1: Có thể chia các số nguyên liên tiếp từ 1 đến 50 thành các nhóm rời nhau sao cho trong mỗi nhóm, số lớn nhất bằng tổng các số còn lại trong nhóm được hay không?
Giải
Bài 2: Có 17 cầu thủ và 15 cổ động viên xếp thành một hàng ngang. Chứng minh rằng có ít nhất 2 cầu thủ mà giữa họ có đúng 5 người khác đứng xen vào.
Giải
Giả sử đánh số 17 cầu thủ và 15 cổ động viên từ 1 đến 32 và chia thành các nhóm:
Nhóm 1: 1,7,13,19,25,31
Nhóm 2: 2,8,14,20,26,32
Nhóm 3: 3,9,15,21,27
Nhóm 4: 4,10,16,22,28
Nhóm 5: 5,11,17,23,29
Nhóm 6: 6,12,18,24,30
Coi 6 nhóm như 6 chuồng chim, 17 cầu thủ như 17 con chim bồ câu. Theo định lý Dirichlet có ít nhất 4 cầu thủ thuộc cùng 1 nhóm. Vì nếu chỉ có 3 cầu thủ thuộc cùng 1 nhóm thì chưa thoả mãn yêu cầu đề bài.
Ví dụ ta xét nhóm 1:
Trường hợp 1: 1,7,13,25
Trường hợp 2: 1,7,13,31
Trường hợp 3: 1,7,13,19
Trường hợp 4: 7,13,19,25
Trường hợp 5: 7,13,19,31
Trường hợp 6: 13,19,25,31
Như vậy trong mọi trường hợp luôn có 2 cầu thủ mà giữa chúng có 5 cổ động viên xen vào.
Bài 3: Lấy 21 số nguyên dương có giá trị không lớn hơn 40. Chứng minh rằng có ít nhất 6 cặp số mà hiệu giữa chúng có giá trị bằng nhau.
Giải
Cứ 2 số tạo thành 1 cặp và tạo thành 1 hiệu, lấy 21 số nên tạo thành \(C_{21}^2=210\) cặp(coi như 210 con chim bồ câu)
Hiệu 2 số có giá trị nhỏ nhất là: 1
Hiệu 2 số có giá trị lớn nhất là: 39(coi như 39 chuồng chim)
Theo nguyên lý Dirichlet có ít nhất \(] \frac{210}{39}=6 [\). Vậy có ít nhất 6 cặp thuộc cùng 1 nhóm tức là có ít nhất 6 cặp số mà hiệu giữa chúng có giá trị bằng nhau.
Bài 4: Chứng minh rằng trong số 9 số khác nhau lấy từ {1, 2, …, 225} có ít nhất 2 số x và y sao cho \(0<|\sqrt{x} -\sqrt{y}|<2\)
Giải
Xếp các số thoả mãn điều kiện \(0<|\sqrt{x} -\sqrt{y}|<2\) vào thành 1 nhóm:
Nhóm 1: {1,2,…,8}
Nhóm 2: {9,10,..,24}
Nhóm 3: {25,26,..,48}
Nhóm 4: {49,50,..,80}
Nhóm 5: {81,82,..,120}
Nhóm 6: {121,122,..,168}
Nhóm 7: {169,..,224}
Nhóm 8: {225}
Lấy 9 số mà có 8 nhóm => Theo nguyên lý Dirichlet có ít hất 2 số thuộc cùng 1 nhóm.
Bài 5: Chứng minh rằng trong số 10 người bất kỳ luôn tồn tại 2 người có tổng số hoặc hiệu số tuổi của họ chia hết cho 17.
Giải
Chọn ra các cặp sao cho tổng các cặp bằng 17
Nhóm 1:(0,0)
Nhóm 2:(1,16)
Nhóm 3:(2,15)
Nhóm 4:(3,14)
Nhóm 5:(4,13)
Nhóm 6:(5,12)
Nhóm 7:(6,11)
Nhóm 8:(7,10)
Nhóm 9:(8,9)
Coi 9 nhóm như 9 chuồng chim bồ câu, 10 người coi như 10 con chim bồ câu. Theo nguyên lý Dirichlet tồn tại ít nhất 2 người mà có tổng hoặc hiệu số tuổi chia hết cho 17
Bài 6: Cho A là một tập gồm các chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Chứng minh rằng trong các số có 4 chữ số lấy từ tập A mà các chữ số tạo thành 1 dãy giảm sẽ có ít nhất 9 số có tổng các chữ số bằng nhau
Giải
Cứ 4 chữ số tạo thành 1 tập con và tạo thành dãy giảm => Các cách để sắp xếp sao cho các chữ số tạo thành dãy giảm là: \(C_{10}^4\) = 210 cách (coi như 210 con chim bồ câu)
Các tập con có tổng bằng nhau tạo thành 1 nhóm:
Nhóm 1: tổng bằng 6 (3,2,1,0)
Nhóm 2: tổng bằng 7
…
Nhóm 25: tổng bằng 30 (9,8,7,6)
Coi 25 nhóm như 25 chuồng chim bồ câu. Theo nguyên lý Dirichlet có ít nhất \(] \frac{210}{30}=9 [\) tập con có tổng bằng nhau.
Bài viết của mình đến đây là kết thúc. Hy vọng với tài liệu trên các bạn đã biết cách giải bài tập nguyên lý dirichlet cơ bản trong môn toán rời rạc. Cảm ơn các bạn đã tham khảo bài viết trên ttnguyen.net. Chúc các bạn học tập tốt!
Bài viết cùng chủ đề: