Trong thống kê, giá trị trung bình là một công cụ quan trọng giúp xác định sự khác biệt đáng kể giữa các nhóm dữ liệu. Bài viết này sẽ hướng dẫn bạn cách áp dụng công thức kiểm định giả thuyết về giá trị trung bình và giải một số bài tập cụ thể.
Xem thêm:
1. Khái niệm kiểm định giả thuyết về giá trị trung bình
Kiểm định giả thuyết về giá trị trung bình được sử dụng để so sánh trung bình mẫu với một giá trị trung bình giả định hoặc giữa hai trung bình mẫu. Phương pháp này giúp xác định xem sự khác biệt có mang tính chất ngẫu nhiên hay có ý nghĩa thống kê.
2. Công thức kiểm định giả thuyết về giá trị trung bình
Giả sử một tổng thể có giá trị trung bình \(\mu \). Để kiểm định giả thuyết về giá trị trung bình, ta thực hiện các bước sau:
2.1. Giả thuyết thống kê
- Giả thuyết không (\(H_0\)): \(\mu = \mu_0\)
- Giả thuyết thay thế (\(H_1\)): \(\mu \neq \mu_0\), \(\mu > \mu_0\) hoặc \(\mu < \mu_0\)
2.2. Công thức tính chỉ số kiểm định
Trường hợp đã biết phương sai tổng thể (\( \sigma_0^{2} \)):
\(Z_{qs}=\frac{\left( \overline{X}-\mu_0 \right)\sqrt{n} }{\sigma_0}\) so sánh với \(W_{\alpha}\) để kết luận:
- Nếu \(Z_{qs} \in W_{\alpha}\) thì bác bỏ H0 và thừa nhận H1.
- Nếu \(Z_{qs} \notin W_{\alpha}\) thì chưa có cơ sở để bác bỏ H0.
Trường hợp chưa biết phương sai tổng thể:
\(t=\frac{\overline{X}-\mu_0 }{\frac{S}{\sqrt{n}}}\)Trong đó:
- \(\overline{X}\): Trung bình mẫu
- \(\mu_0\): Giá trị trung bình giả định
- \(\sigma_0\): Độ lệch chuẩn tổng thể
- \(S\): Độ lệch chuẩn mẫu hiệu chỉnh
- \(n\): Kích thước mẫu
2.3. Miền bác bỏ
| \(H_0\) – Tiêu chuẩn | \(H_1\) | Miền bác bỏ \(W_{\alpha}\) |
| \(H_0: \mu = \mu_0\)
\(Z=\frac{\overline{X}-\mu_0}{S/\sqrt{n}}\) |
\(\mu \neq \mu_0\) | \(\left\{ Z:\left| Z \right| >t_{\alpha/2}^{(n-1)}\right\}\) |
| \(\mu > \mu_0\) | \(\left\{ Z:\left| Z \right| >t_{\alpha}^{(n-1)}\right\}\) | |
| \(\mu < \mu_0\) | \(\left\{ T: < -t_{\alpha}^{(n-1)}\right\}\) |
3. Bài tập kiểm định giả thuyết về giá trị trung bình có lời giải
Bài 1: Kiểm định trọng lượng sản phẩm đóng gói
– Trường hợp đã biết phương sai tổng thể:
Đề bài: Trọng lượng mỗi gói sản phẩm do một nhà máy sản xuất là biến ngẫu nhiên phân phối chuẩn với độ lệch chuẩn 36g và trọng lượng trung bình 453g. Kiểm tra ngẫu nhiên 81 gói sản phẩm đó thấy trọng lượng trung bình là 448g. Với mức ý nghĩa 5% có thể kết luận các sản phẩm đóng gói có bị thiếu hay không.
Giải

Bài 2: Kiểm định năng suất lúa
– Trường hợp đã chưa biết phương sai tổng thể:
Đề bài: Thu hoạch thử 41 thửa ruộng trồng lúa, tính được năng suất trung bình 39,5 tạ/ha và độ lệch chuẩn mẫu hiệu chỉnh 1,2 tạ/ha. Trước đây, giống lúa này cho năng suất 39 tạ/ha. Với mức ý nghĩa 5%, có thể cho rằng năng suất lúa đã tăng lên hay không? Biết rằng năng suất lúa là biến ngẫu nhiên tuân theo quy luật chuẩn.
Giải
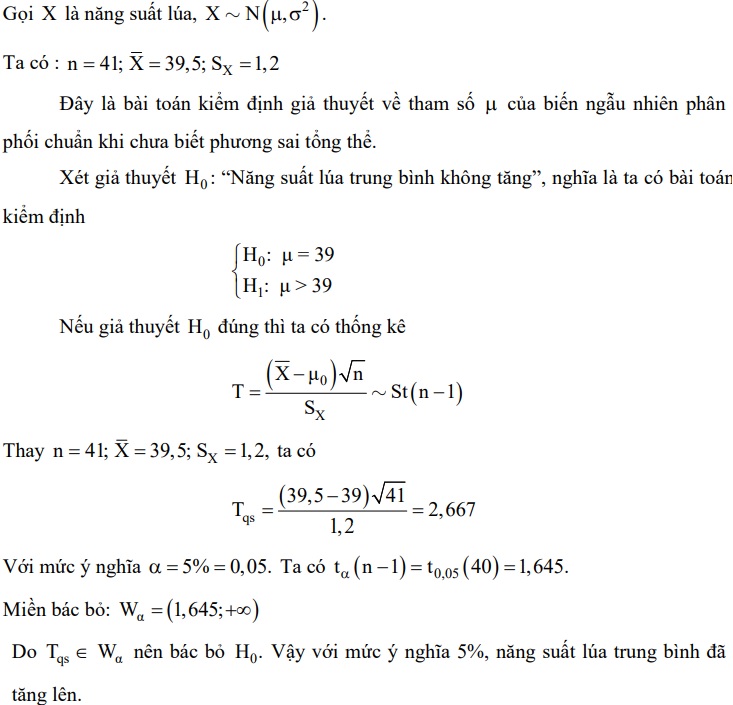
Bài 3: Kiểm định hoạt động của máy đóng gói
Đề bài: Một máy đóng gói các sản phẩm có khối lượng 1kg. Nghi ngờ máy hoạt động
không bình thường, người ta chọn ra một mẫu ngẫu nhiên gồm 100 sản phẩm thì thấy
như sau :
| Khối lượng | 0,95 | 0,97 | 0,99 | 1,01 | 1,03 | 1,05 |
| Số gói | 9 | 31 | 40 | 15 | 3 | 2 |
Với mức ý nghĩa 5%, hãy kết luận về nghi ngờ trên.
Giải

Bài 4: Kiểm định doanh số bán hoa hồng
Đề bài: Quan sát số hoa hồng bán ra trong một ngày của một cửa hàng bán hoa sau
một thời gian, người ta ghi được số liệu sau :
| Số hoa hồng | 12 | 13 | 15 | 16 | 17 | 18 | 19 |
| Số ngày | 3 | 2 | 7 | 7 | 3 | 2 | 1 |
Sau khi tính toán, ông chủ cửa hàng nói rằng nếu trung bình một ngày không bán
được 15 đoá hoa thì chẳng thà đóng cửa còn hơn. Dựa vào số liệu trên, anh (chị) hãy kết
luận giúp ông chủ cửa hàng xem có nên tiếp tục bán hay không ở mức ý nghĩa 5%.
Giải

Bài viết đã giới thiệu công thức kiểm định giả thuyết về giá trị trung bình và hướng dẫn giải các bài tập minh họa. Hy vọng nội dung này sẽ giúp bạn nắm vững cách áp dụng kiểm định giả thuyết trong xác suất thống kê. Cảm ơn các bạn đã tham khảo trên ttnguyen.net.