Chu trình Euler là một trong những khái niệm quan trọng trong lý thuyết đồ thị. Trong bài viết này, TTnguyen sẽ cùng bạn tìm hiểu lý thuyết và một số kiến thức cơ bản cùng các dạng bài tập chu trình euler trong môn toán rời rạc. Đây là các bài tập cơ bản thường hay gặp nhất trong quá trình học.
Xem thêm:
bài tập toán rời rạc chương 1 có lời giải
I. Đường đi và chu trình Euler
Định nghĩa
- Chu trình Euler là chu trình trong đồ thị \(G=(V,E)\) đi qua mỗi cạnh của đồ thị đúng một lần và kết thúc tại đỉnh xuất phát.
- Đường đi Euler là đường đi trong đồ thị G, đi qua mỗi cạnh đúng một lần nhưng không nhất thiết phải quay lại điểm xuất phát.
Phân loại đồ thị
- Đồ thị Euler là đồ thị chứa chu trình Euler.
- Đồ thị nửa Euler là đồ thị không có chu trình Euler nhưng chứa đường đi Euler.
Ví dụ: Xét các đồ thị vô hướng sau: Xét các đồ thị G1, G2, G3
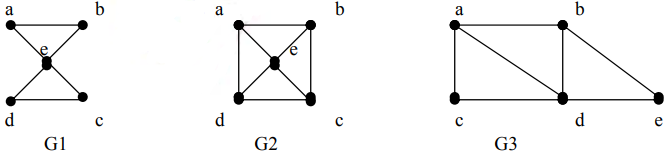
Đồ thị G1 là đồ thị Euler vì nó có chu trình Euler a, e, c, d, e, b, a.
Đồ thị G3 không có chu trình Euler nhưng chứa đường đi Euler a, c, d, e, b, d, a, b vì thế G3 là nửa Euler.
G2 không có chu trình Euler cũng như đường đi Euler.
II. Điều kiện để có chu trình Euler
Đồ thị vô hướng:
- Để có chu trình Euler: Tất cả các đỉnh phải có bậc chẵn.
- Để có đường đi Euler: Đồ thị phải liên thông và có không quá hai đỉnh bậc lẻ.
Đồ thị có hướng:
- Để có chu trình Euler: Mọi đỉnh phải có bậc vào bằng bậc ra.
- Để có đường đi Euler: Phải có đúng một đỉnh có bậc vào lớn hơn bậc ra và một đỉnh có bậc ra lớn hơn bậc vào.
III. Thuật toán Euler – Cách tìm chu trình và đường đi Euler
Chu trình Euler:
- Xuất phát từ một đỉnh bất kỳ.
- Di chuyển qua các cạnh chưa đi qua, đánh dấu mỗi cạnh đã đi.
- Quay lại đỉnh xuất phát để hoàn thành chu trình.
Đường đi Euler:
- Bắt đầu từ đỉnh có bậc lẻ
- Thực hiện các bước tương tự như tìm chu trình Euler.
IV. Bài tập tìm chu trình Euler
Bài 1: Xét các đồ thị có hướng H1, H2, H3
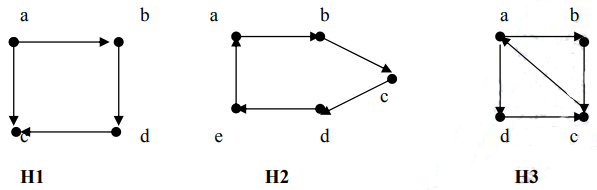
Đồ thị H2 là đồ thị Euler vì nó chứa chu trình Euler a, b, c, d, e, a vì vậy nó là đồ thị Euler.
Đồ thị H3 không có chu trình Euler nhưng có đường đi Euler a, b, c, a, d, c nên nó là đồ thị nửa Euler.
Đồ thị H1 không chứa chu trình Euler cũng như chu trình Euler
V. Bài tập đồ thị Euler
Đồ thị đủ n đỉnh:
Đồ thị đủ n đỉnh kí hiệu là Kn là đồ thị đơn vô hướng, mà giữa 2 đỉnh bất kì của nó luôn có cạnh nối
Có tất cả cách cạnh là n(n-1)/2. Bậc của các đỉnh bằng nhau và bằng n-1
Cây bao trùm(cây khung):
Cây bao trùm là đồ thị con, không có chu trình chứa tất cả các đỉnh của đồ thị đó
Bài 1: Cho G là đồ thị vô hướng, đủ và có 9 đỉnh
- Có bao nhiêu đồ thị con và bao nhiêu đồ thị bộ phận?
- Có bao nhiêu cây bao trùm có một đỉnh bậc 6 và một đỉnh bậc 3?
- Có bao nhiêu đồ thị con là đồ thị Euler, không phải đồ thị Euler?
- Có bao nhiêu cây bao trùm có một đỉnh bậc 6?
- Có bao nhiêu số đồ thị con có đỉnh là số lẻ?
- Có bao nhiêu đồ thị con là đồ thị chính quy bậc 5?
- Có bao nhiêu cây có độ dài lớn hơn 6?
Lời giải
a) Có bao nhiêu đồ thị con và bao nhiêu đồ thị bộ phận?
– Đồ thị con: là bỏ đi một số đỉnh và các cạch liên quan liên quan đến đỉnh đó
- Bớt đi 1 đỉnh: có \( \ C_{9}^1 \) cách bớt tương ứng với 9 đồ thị con
- Bớt đi 2 đỉnh: có \( \ C_{9}^2 \) cách bớt
- Bớt đi 3 đỉnh: có \( \ C_{9}^3 \) các bớt
- Bớt đi 4 đỉnh: có \( \ C_{9}^4 \) cách bớt
- Bớt đi 5 đỉnh: có \( \ C_{9}^5 \) cách bớt
- Bớt đi 6 đỉnh: có \( \ C_{9}^6 \) cách bớt
- Bớt đi 7 đỉnh: có \( \ C_{9}^7 \) cách bớt
- Bớt đi 8 đỉnh: có \( \ C_{9}^8 \) cách bớt
=> Số đồ thị con: \(\sum_{i=1}^8 \ C_{9}^i = 510 \) (đồ thị)
– Đồ thị bộ phận: bớt 1 một số cung và giữ nguyên số đỉnh
Số cạnh là: 9.8/2=36 (cạnh)
Bớt đi 1 cạnh có \( \ C_{36}^1 \) cách bớt
…
Bớt đi 36 cạnh có cách bớt
=> Số đồ thị bộ phận là: \( \sum_{i=1}^36 \ C_{16}^i \) (đồ thị)
b) Có bao nhiêu cây bao trùm có một đỉnh bậc 6 và một đỉnh bậc 3?
Chọn 1 đỉnh trong 9 đỉnh để làm 1 đỉnh bậc 6 có \( \ C_{9}^1 =9 \) cách.
Còn lại 8 đỉnh, ta chọn 6 đỉnh để nối với đỉnh bậc 6 có \( \ C_{8}^6 = 28 \) cách.
Còn lại 2 đỉnh, thì 2 đỉnh đó phải gắn cùng với 1 đỉnh => Có \( \ C_{6}^1 = 6 \) cách.

Vậy số cây thoả mãn là: 9.28.6 =1512 (cây)
c) Có bao nhiêu đồ thị con là đồ thị Euler, không phải đồ thị Euler?
Số đồ thị con Euler là: \( \ C_{9}^3+C_{9}^5+C_{9}^7=246 \) (đồ thị)
Số đồ thị con không phải Euler là: 510-246= 264 (đồ thị)
d) Có bao nhiêu cây bao trùm có một đỉnh bậc 6
Chọn 1 đỉnh trong 9 đỉnh để làm 1 đỉnh bậc 6 có \( \ C_{9}^1 \)= 6=9 cách
Còn lại 8 đỉnh, ta chọn 6 đỉnh để nối với đỉnh bậc 6 có \( C_{6}^6 \)= 6=28 cách
Còn lại 2 đỉnh, thì 2 đỉnh:
- gắn cùng với đỉnh => Có \( C_{6}^1 \)=6 cách
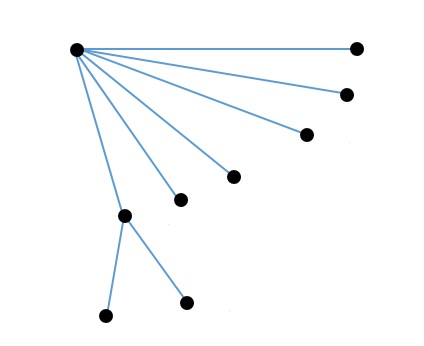
- gắn với 2 đỉnh khác nhau trong 6 đỉnh: \( 2!.C_{6}^2 \)=30 cách
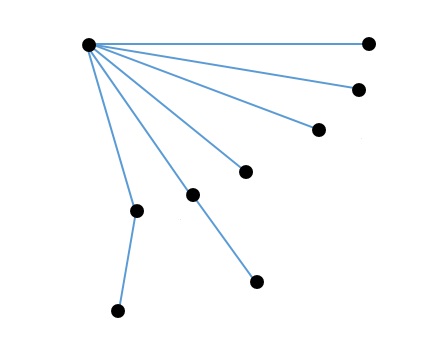
- gắn với 1 đỉnh và đỉnh còn lại gắn với đỉnh đó: 6.2=12

Vậy số cây thoả mãn là: 9.28.(6+12+30)= 12096 cây
e) Có bao nhiêu số đồ thị con có đỉnh là số lẻ
Đồ thị con có đỉnh là số lẻ là: \( C_{9}^1+C_{9}^3+C_{9}^5+C_{9}^7 \)
f) Có bao nhiêu đồ thị con là đồ thị chính quy bậc 5?
-Đồ thị chính quy bậc 5: đồ thị bậc các đỉnh bằng nhau và bằng 5, nên đồ thị phải có 6 đỉnh: \( C_{9}^5 \)
g) Có bao nhiêu cây có độ dài lớn hơn 6?
Cây có độ dài lớn hơn 6 thì số đỉnh phải là: 8,9
=> Số cây thoả mãn là: \(T_8+T_9=8^6+9^7\)
Bài 2: Một đơn đồ thị liên thông có 10 mặt, tất cả các đỉnh đều có bậc bằng 4, tìm số đỉnh của đồ thị.
Lời giải
Gọi f là số miền của mặt phẳng bị chia bởi biểu diễn phẳng của đồ thị, e là số cạnh và v là số đỉnh của đồ thị
Ta có tổng bậc của đồ thị bằng 2 lần số cạnh, tức là : 2e = 4v => e=2v
Mặt khác, ta có : f = e – v + 2 => 10 = 2v – v + 2 => v=8
Vậy đồ thị có 8 đỉnh và 16 cạnh.
Bài 3: Một đơn đồ thị liên thông có 10 mặt, tất cả các đỉnh đều có bậc bằng 4, tìm số đỉnh của đồ thị.
Lời giải
Gọi f là số miền của mặt phẳng bị chia bởi biểu diễn phẳng của đồ thị, e là số cạnh và v là số đỉnh của đồ thị
Ta có tổng bậc của đồ thị bằng 2 lần số cạnh, tức là : 2e = 4v => e=2v
Mặt khác, ta có : f = e – v + 2 => 10 = 2v – v + 2 => v=8
Vậy đồ thị có 8 đỉnh và 16 cạnh.
Hy vọng qua bài viết vừa rồi các bạn đã nắm vững kiến thức về đồ thị euler, đồ thị đầy đủ, đồ thị vô hướng và chu trình Euler. Nếu có bất kì thắc mắc nào thì đừng ngần ngại liên hệ với mình nhé. Chúc các bạn học tập môn toán rời rạc này thật tốt!
Bài viết cùng chủ đề: