[C++] Kiểm tra số chính phương - Thuật toán & CODE mẫu

Số chính phương là một khái niệm thú vị và hữu ích, có ứng dụng rộng trong việc giải quyết các bài toán và lập trình. Trong bài viết này, chúng ta sẽ tìm hiểu cách nhận biết số chính phương và thuật toán kiểm tra số chính phương c++ đơn giản, dễ hiểu nhất. Bắt đầu thôi!

Bài trước: Bài 14: viết chương trình tính tổng theo công thức S(n) = 1+1/3+1/5+1/7…+1/(2*n-1) trong c++.

Nội dung

1. Số chính phương là gì?

Định nghĩa

Số chính phương hay square number là số bằng bình phương đúng của một số nguyên.

Hay hiểu đơn giản, số chính phương là một số tự nhiên có căn bậc hai cũng là một số tự nhiên. Số chính phương về bản chất là bình phương của một số tự nhiên nào đó.

Ví dụ, 1, 4, 9, 16, 25, và 36 là các số chính phương, vì căn bậc hai của chúng (1, 2, 3, 4, 5 và 6) đều là các số nguyên.

Một số tính chất của số chính phương

Các số chính phương luôn là các số không âm vì căn bậc hai của một số âm là không xác định.
Kết quả của việc cộng hai số chính phương lại là một số chính phương.
Số chính phương cuối cùng của một dãy số chính phương liên tiếp luôn là một số lẻ.

2. Bài toán kiểm tra số chính phương

Bài 15: Số chính phương hay còn gọi là số hình vuông, là số tự nhiên có căn bậc 2 là một số nguyên. Hãy viết chương trình nhập vào các số nguyên đến khi gặp 0 thì dừng.

Đưa ra các kết quả sau: số lượng số chính phương đã nhập (nếu không có số nào thì trả về “không có số chính phương nào được nhập”), trung bình cộng các số chính phương chẵn (nếu nó là một số chẵn).

3. Thuật toán kiểm tra số chính phương c++

3.1. Viết hàm kiểm tra và tính tổng số chính phương

Vòng lặp do-while được sử dụng để nhập và kiểm tra các số nguyên từ người dùng cho đến khi nhập giá trị 0. Trong vòng lặp này, số n được kiểm tra xem có phải là số chính phương hay không. Nếu n là số chính phương, biến dem được tăng lên 1 và nếu n là số chẵn, tổng sum và soluongChan được cập nhật. Vòng lặp sẽ tiếp tục cho đến khi người dùng nhập giá trị 0.
Sử dụng hàm tính căn bậc sqrt() trong thư viện math. Nếu sqrt(n)*sqrt(n) = n thì tức là n là số chính phương. Nếu như n < 1 thì n sẽ không phải là số chính phương.

if (n > 0 && n == sqrt(n) * sqrt(n)) {
  cout << "n la so chinh phuong";
} else {
  cout << "n khong phai la so chinh phuong";
}

3.2 in ra số chính phương trong mảng c++

Sau khi kết thúc vòng lặp, chương trình sẽ kiểm tra giá trị của biến dem để xác định có số chính phương nào hay không. Nếu dem khác 0, chương trình sẽ in ra số lượng số chính phương và tính trung bình cộng TBC của các số chính phương chẵn. Nếu dem bằng 0, chương trình sẽ in ra thông báo không có số chính phương nào.

4. Code kiểm tra số chính phương c

#include<bits/stdc++.h>

using namespace std;
int main() {
  int i, n, sum = 0, dem = 0, soluongChan = 0;
  float TBC;
  do {
    cout << "nhap so nguyen n: ";
    cin >> n;
    if (n > 0 && n == sqrt(n) * sqrt(n)) {
      dem++;
      if (n % 2 == 0) {
        sum = sum + n;
        soluongChan++;
      }
    }
  } while (n != 0);
  if (dem != 0) {
    cout << "Co " << dem << " so chinh phuong" << endl;
    TBC = sum / soluongChan;
    cout << "Trung binh cong cac so chinh phuong chan la: " << TBC;
  } else cout << "khong co so chinh phuong nao";
}

5. Kết quả

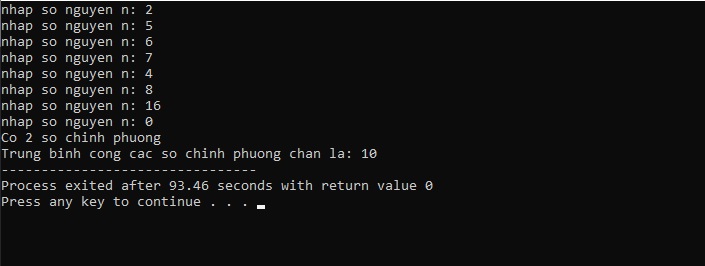
Trên đây là một ví dụ về việc sử dụng ngôn ngữ lập trình C++ để đếm số chính phương và tính trung bình cộng của các số chính phương chẵn. Bằng cách sử dụng vòng lặp và kiểm tra điều kiện, chương trình cho phép người dùng nhập các số nguyên và xác định xem chúng có phải là số chính phương hay không.

Chúng ta đã tìm hiểu cách sử dụng hàm sqrt() để kiểm tra tính chính phương của một số. Chương trình cũng đếm số lượng số chính phương và tính trung bình cộng của các số chính phương chẵn.

Hy vọng rằng ví dụ trên đã giúp bạn hiểu thêm về số chính phương và cách áp dụng nó trong ngôn ngữ lập trình C++. Cảm ơn bạn đã theo dõi trên ttnguyen.net và chúc bạn thành công!

Tải full bài tập thực hành lập trình C/C++ có lời giải

Bài tiếp theo: Bài 17 (TH-CSLT-01). Hãy viết chương trình nhập vào một dãy số đến khi gặp số 0 thì dừng, sau đó tách mảng c++ số chẵn và số lẻ ra 02 mảng khác nhau. Tính trung bình cộng các số chẵn dương và trung bình cộng các số lẻ âm.

Câu hỏi liên quan

Các ước là số chính phương của 180

Ước số của 180 là: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180.

Các ước số chính phương của 180 là: 1, 4, 9, 36.

Vậy, các ước số chính phương của 180 là 1, 4, 9 và 36.

Số chính phương nhỏ nhất có 3 chữ số

Số chính phương nhỏ nhất có 3 chữ số là 100, vì căn bậc hai của 100 bằng 10, và 10 là một số nguyên.

Số chính phương lớn nhất có 3 chữ số

Số chính phương lớn nhất có 3 chữ số là 961. Căn bậc hai của 961 bằng 31, và 31 là một số nguyên.

0 có phải là số chính phương không

Không, 0 không phải là số chính phương. Một số chính phương phải là một số nguyên dương và có căn bậc hai là một số nguyên. Căn bậc hai của 0 là 0, nhưng 0 không thỏa mãn điều kiện số nguyên dương, vì vậy nó không được coi là số chính phương.

1 có phải số chính phương không

Có, 1 là một số chính phương. Một số chính phương là một số nguyên dương có căn bậc hai cũng là một số nguyên. Căn bậc hai của 1 là 1, và 1 là một số nguyên, vì vậy nó được coi là số chính phương.

[C++] Kiểm tra số chính phương – Thuật toán & CODE mẫu