Việc đổi thứ tự lấy tích phân là một khái niệm quan trọng giúp giải quyết nhiều bài toán phức tạp mà không thể giải quyết bằng cách lấy tích phân theo thứ tự thông thường. Trong bài viết này, chúng ta sẽ tìm hiểu về đổi thứ tự lấy tích phân và một số bài tập vận dụng
Xem thêm:
bài tập tính tích phân kép cơ bản
1. Đổi thứ tự lấy tích phân là gì?
Đổi thứ tự lấy tích phân là quá trình thay đổi thứ tự của phép tích phân các hàm đa biến để tối ưu hóa quá trình tính toán và tăng độ chính xác của kết quả.
2. Bài tập đổi thứ tự lấy tích phân có lời giải
Bài 1: Thay đổi thứ tự lấy tích phân:
\(\int_{0}^{1}dx\int_{\sqrt{2x-x^2}}^{1}f(x,y)dy\)Lời giải
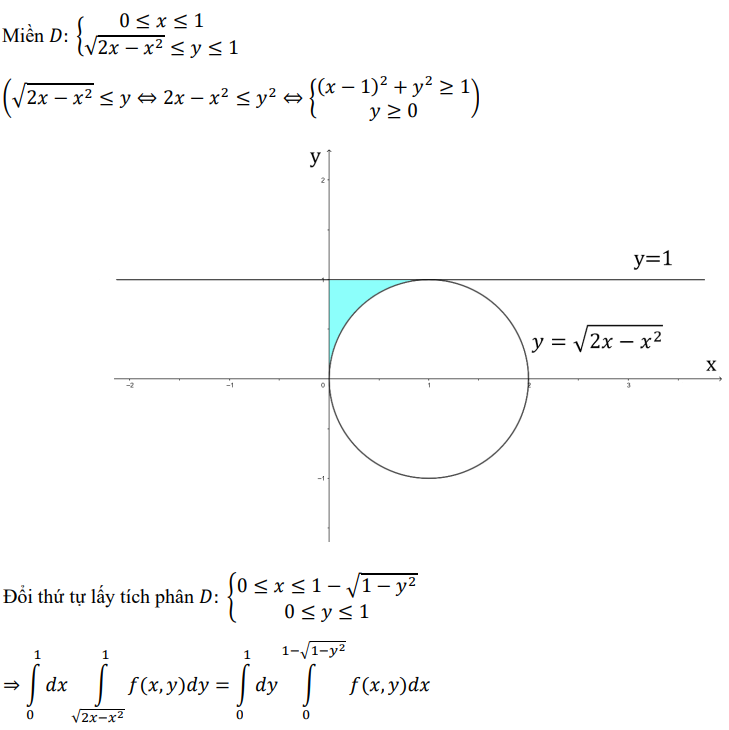
Bài 2: Đổi thứ tự lấy tích phân:
\(\int_{0}^{1}dx\int_{x^3}^{\sqrt{x}}f(x,y)dy\)Lời giải
Miền lấy tích phân:
\(D:\begin{cases}0\le x\le 1 \\
x^2\le y\le \sqrt[3]{x}
\end{cases}\)
Dựa vào hình vẽ, ta viết lại miền lấy tích phân:
\(\int_{0}^{1}dx\int_{x^3}^{\sqrt{x}}f(x,y)dy=\int_{0}^{1}dy\int_{y^2}^{\sqrt[3]{y}}f(x,y)dx\)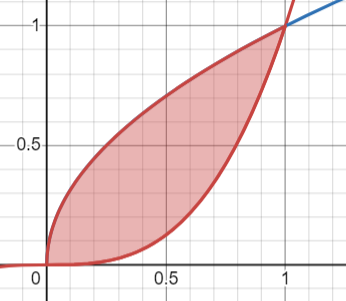
Bài 3: Đổi thứ tự lấy tích phân:
\(\int_{0}^{1}dy\int_{2-y}^{1+\sqrt{1-y^2}}f(x,y)dx\)Lời giải
Miền lấy tích phân:
\(D:\begin{cases}0\le y\le 1 \\
2-y\le x\le 1+\sqrt{1-y^2}
\end{cases}\)
Dựa vào hình vẽ, ta viết lại miền lấy tích phân:
\(D:\begin{cases}1\le x\le 2 \\
2-x\le y\le \sqrt{2x-x^2}
\end{cases}\)
Kết quả đổi thứ tự lấy tích phân:
\(\int_{0}^{1}dy\int_{2-y}^{1+\sqrt{1-y^2}}f(x,y)dx=\int_{1}^{2}dx\int_{2-x}^{\sqrt{2x-x^2}}f(x,y)dy\)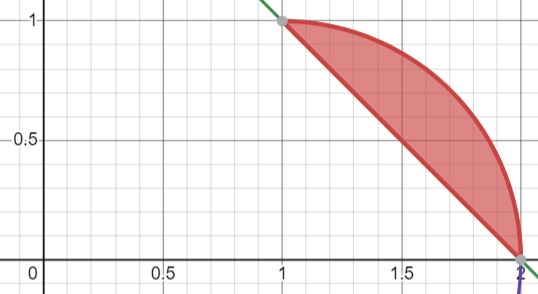
Bài 4: Đổi thứ tự lấy tích phân:
\(\int_{0}^{\frac{\pi}{2}}dx\int_{sinx}^{1+x^2}f(x,y)dy\)Lời giải
Miền lấy tích phân:
\(D:\begin{cases}0\le x\le \frac{\pi}{2} \\
sinx \le y \le 1 + x^2
\end{cases}\)
Ta có: \( D = D_1 \cup D_2 \), trong đó:
\(D_1:\begin{cases}
0\le y\le 1 \\
0\le x\le arcsiny
\end{cases} \\ \) và
\(D_2:\begin{cases}
1\le y\le 1+\frac{\pi^2}{2} \\
\sqrt{y-1}\le x\le \frac{\pi}{2}
\end{cases}\)
Kết quả đổi thứ tự lấy tích phân:
\(\int_{0}^{\frac{\pi}{2}}dx\int_{sinx}^{1+x^2}f(x,y)dy=\int_{0}^{1}dy\int_{0}^{arcsiny}f(x,y)dx + \int_{1}^{1+\frac{\pi^2}{4}}dy\int_{\sqrt{y-1}}^{\frac{\pi}{2}}f(x,y)dx\)Trên đây là lý thuyết và một số bài tập đổi lấy thứ tự tích phân có lời giải. Cảm ơn bạn đã tham khảo giải tích 2 trên ttnguyen.net.
