Thuật toán Prim giải tay toán rời rạc

Thuật toán Prim là một trong những thuật toán quan trọng trong toán rời rạc, được sử dụng để tìm cây khung nhỏ nhất của một đồ thị liên thông có trọng số. Trong bài viết này, TTnguyen sẽ cùng bạn tìm hiểu lý thuyết, cách hoạt động và các bước giải tay thuật toán.

Xem thêm:

bài tập thuật toán dijkstra có lời giải tìm đường đi ngắn nhất

chu trình euler

lý thuyết đồ thị toán rời rạc

Nội dung

I. Thuật toán Prim là gì?

Thuật toán Prim (Prim’s Algorithm) là một thuật toán tìm cây khung nhỏ nhất (Minimum Spanning Tree) của một đồ thị liên thông có trọng số, bằng cách chọn một tập hợp các cạnh sao cho:

Tạo thành một cây bao gồm tất cả các đỉnh của đồ thị.
Tổng trọng số của các cạnh là nhỏ nhất trong tất cả các cây có thể được tạo ra từ đồ thị đó.

Một số khái niệm:

Cây khung: một tập các cạnh sao cho tập cạnh này không tồn tại chu trình và liên thông
Cây khung nhỏ nhất: là cây khung mà tổng trọng số các cạnh thuộc cây khung là nhỏ nhất

II. Cách hoạt động của thuật toán Prim

Quy trình cơ bản:

Bắt đầu: Chọn một đỉnh bất kỳ s trong đồ thị làm điểm xuất phát.
Bước đầu tiên: Tìm cạnh có trọng số nhỏ nhất nối từ đỉnh s đến một đỉnh khác y trong đồ thị. Thêm cạnh (s, y) này vào cây khung, đồng thời thêm đỉnh y vào tập đỉnh của cây khung.
Tiếp tục: Từ các đỉnh đã được thêm vào cây khung (ở đây là s và y), tìm cạnh có trọng số nhỏ nhất nối một trong các đỉnh này đến một đỉnh chưa thuộc cây khung. Cạnh này sẽ nối đến một đỉnh thứ ba z. Lúc này, cây khung đã có 3 đỉnh và 2 cạnh.
Lặp lại: Tiếp tục thêm vào cây khung cạnh có trọng số nhỏ nhất nối các đỉnh trong cây khung hiện tại với một đỉnh chưa thuộc cây khung. Lặp quá trình này cho đến khi cây khung có đủ n−1 cạnh (với n là số đỉnh của đồ thị).
Kết quả: Khi quá trình hoàn tất, ta thu được một cây khung nhỏ nhất của đồ thị, với tổng trọng số của các cạnh là nhỏ nhất.

Các bước thực hiện:

Giả sử đồ thị có 5 đỉnh:

Bước đầu tiên: Chọn đỉnh A làm điểm bắt đầu.
Bước tiếp theo: Tìm cạnh có trọng số nhỏ nhất nối từ A đến B.
Lặp lại: Tìm cạnh nhỏ nhất từ cây khung đến các đỉnh còn lại.
Hoàn thành: Cây khung bao gồm tất cả các đỉnh.

Đỉnh	Cạnh chọn	Tổng trọng số
A	(A,B)	5
B	(B,C)	8
…	…	…

III. Độ phức tạp của thuật toán Prim

Độ phức tạp thời gian của thuật toán Prim là O(E log V), trong đó E là số cạnh và V là số đỉnh trong đồ thị.

Độ phức tạp không gian của thuật toán Prim là O(V + E).

IV. Bài tập giải tay thuật toán Prim

Bài 1: Dùng thuật toán Prim tìm cây khung nhỏ nhất của đồ thị có ma trận trọng số sau:

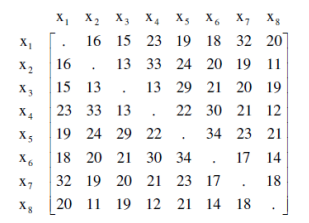
Giải

Tập cạnh của cây khung nhỏ nhất cần tìm là T={(X1,X3), (X3,X2), (X2,X8), (X8,X4), (X8,X6), (X6,X7), (X1,X5)} trọng số nhỏ nhất bằng : 13+15+12+19+14+17+11 = 101. Cây khung được vẽ như sau:

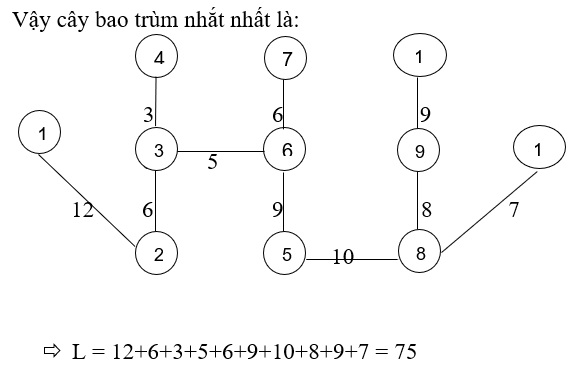
Bài 2: Tìm cây bao trùm ngắn nhất prim:

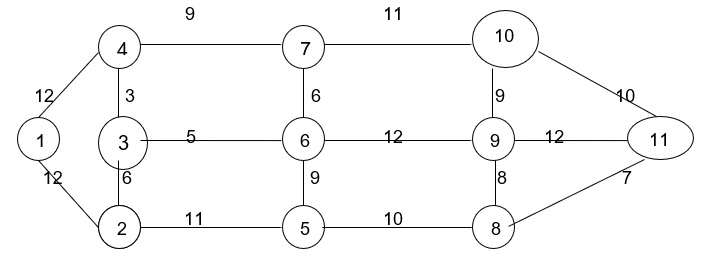
Giải

Bước 1: \( X_1 = { 1}, V_1 = {∅} \)
Bước 2: \( X_2 = { 1,2}, V_2 = {(1,2)} \)
Bước 3: \( X_3 = { 1,2,3}, V_3 = {(1,2),(2,3)} \)
Bước 4: \( X_4 = { 1,2,3,4}, V_4 = {(1,2),(2,3),(3,4)} \)
Bước 5: \( X_5 = { 1,2,3,4,6}, V_5 = {(1,2),(2,3),(3,4),(3,6)} \)
Bước 6: \( X_6 = X_5 ∪ {7}, V_6 = V_5 ∪ {(6,7)} \)
Bước 7: \( X_7 = X_6 ∪ {5}, V_7 = V_6 ∪ {(6,5)} \)
Bước 8: \( X_8 = X_7 ∪ {8}, V_8 = V_7 ∪ {(5,8)} \)
Bước 9: \( X_9 = X_8 ∪ {11}, V_9 = V_8 ∪ {(8,11)} \)
Bước 10: \( X_{10} = X_9 ∪ {9}, V_{10} = V_9 ∪ {(8,9)} \)
Bước 11: còn lại đỉnh 10, đỉnh gần đỉnh 10 nhất là đỉnh \(9 X_{11} = X_{10} ∪ {10}, V_{11} = V_{10} ∪ {(9,10)} \)

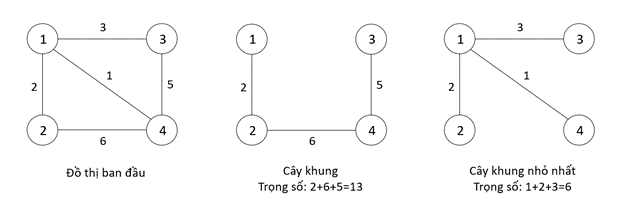
V. So sánh thuật toán Prim và Kruskal

So sánh thuật toán Prim và Kruskal:

Prim: Hiệu quả hơn khi đồ thị có nhiều cạnh (đồ thị dày đặc).
Kruskal: Thích hợp hơn cho đồ thị có số cạnh ít (đồ thị thưa).

Đặc điểm	Prim	Kruskal
Cách tiếp cận	Bắt đầu từ một đỉnh	Bắt đầu từ cạnh nhỏ nhất
Dữ liệu ưu tiên	Hàng đợi ưu tiên	Danh sách cạnh
Hiệu quả	Thích hợp cho đồ thị nhiều cạnh	Thích hợp cho đồ thị ít cạnh

VI. Cài đặt thuật toán Prim bằng c++

1. Mô tả thuật toán Prim

Các bước chính của thuật toán Prim tìm cây phủ nhỏ nhất T của đồ thị liên thông có trọng số G được mô tả như sau:

Bước 1 : T := {v} v là đỉnh bất kỳ.

Bước 2 : Lặp n-1 lần

– Tìm đỉnh rìa v có cạnh e nối T với trọng số nhỏ nhất

– Đưa e vào T

2. Code minh hoạ

#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <math.h>

#include <dos.h>

#define TRUE 1
#define FALSE 0
#define MAX 10000
int a[100][100];
int n, m, i, sc, w;
int chuaxet[100];
int cbt[100][3];
FILE * f;
void nhap(void) {
  int p, i, j, k;
  for (i = 1; i <= n; i++)
    for (j = 1; j <= n; j++)
      a[i][j] = 0;
  f = fopen("baotrum.in", "r");
  fscanf(f, "%d%d", & n, & m);
  printf("\n So dinh: %3d ", n);
  printf("\n So canh: %3d", m);
  printf("\n Danh sach canh:");
  for (p = 1; p <= m; p++) {
    fscanf(f, "%d%d%d", & i, & j, & k);
    printf("\n %3d%3d%3d", i, j, k);
    a[i][j] = k;
    a[j][i] = k;
  }
  for (i = 1; i <= n; i++) {
    printf("\n");
    for (j = 1; j <= n; j++) {
      if (i != j && a[i][j] == 0)
        a[i][j] = MAX;
      printf("%7d", a[i][j]);
    }
  }
  fclose(f);
  getch();
}
void Result(void) {
  for (i = 1; i <= sc; i++)
    printf("\n %3d%3d", cbt[i][1], cbt[i][2]);
}
void PRIM(void) {
  int i, j, k, top, min, l, t, u;
  int s[100];
  sc = 0;
  w = 0;
  u = 1;
  for (i = 1; i <= n; i++)
    chuaxet[i] = TRUE;
  top = 1;
  s[top] = u;
  chuaxet[u] = FALSE;
  while (sc < n - 1) {
    min = MAX;
    for (i = 1; i <= top; i++) {
      t = s[i];
      for (j = 1; j <= n; j++) {
        if (chuaxet[j] && min > a[t][j]) {
          min = a[t][j];
          k = t;
          l = j;
        }
      }
    }
    sc++;
    w = w + min;
    cbt[sc][1] = k;
    cbt[sc][2] = l;
    chuaxet[l] = FALSE;
    a[k][l] = MAX;
    a[l][k] = MAX;
    top++;
    s[top] = l;
    printf("\n");
  }
}
void main(void) {
  clrscr();
  nhap();
  PRIM();
  printf("\n Do dai ngan nhat:%d", w);
  for (i = 1; i <= sc; i++)
    printf("\n %3d%3d", cbt[i][1], cbt[i][2]);
  getch();
}

Tải full bài tập thực hành lập trình C/C++ có lời giải:

VII. Ứng dụng thực tế của thuật toán Prim

Bài toán tìm cây khung nhỏ nhất của một đồ thị là một trong những bài toán tối ưu trên đồ thị có rất nhiều ứng dụng trong thực tế. Để minh họa cho thuật toán này, ta có thể xem xét một số mô hình thực tế điển hình:

Bài toán xây dựng đường giao thông: Giả sử chúng ta cần xây dựng một hệ thống đường bộ để kết nối n thành phố, đảm bảo rằng giữa bất kỳ hai thành phố nào cũng có một con đường. Nhiệm vụ đặt ra là tìm cây khung nhỏ nhất trên đồ thị, trong đó mỗi thành phố là một đỉnh và mục tiêu là tối thiểu hóa tổng chi phí xây dựng hệ thống đường giao thông này.
Bài toán nối mạng máy tính: Giả sử có n máy tính cần kết nối với nhau trong một hệ thống mạng. Biết rằng chi phí kết nối giữa máy i và máy j là c[i,j], với i,j = 1, 2, …, n (thông thường, chi phí này phụ thuộc vào độ dài cáp kết nối). Mục tiêu là tìm ra cách kết nối sao cho tổng chi phí nối mạng là thấp nhất.

Trên đây là lý thuyết và bài tập vận dụng thuật toán prim toán rời rạc. Cảm ơn các bạn đã tham khảo trên ttnguyen.net

Bài viết liên quan:

Thuật toán cờ caro ma trận nxm c++

Thuật toán mã hóa Caesar c++

kiểm tra số chính phương c++

Thuật toán Prim giải tay toán rời rạc | Bài tập có lời giải