Thuật toán Kruskal là một trong những thuật toán cơ bản và hiệu quả nhất để tìm cây khung nhỏ nhất (Minimum Spanning Tree – MST) trong lý thuyết đồ thị. Bài viết dưới đây, TTnguyen sẽ cùng bạn tìm hiểu lý thuyết, bài tập và cách cài đặt thuật toán kruskal bằng ngôn ngữ C++.
Xem thêm:
I. Thuật toán Kruskal là gì?
Khái niệm thuật toán
Thuật toán Kruskal là thuật toán tìm cây khung nhỏ nhất trong một đồ thị liên thông có trọng số, nhận đầu vào là một đồ thị và tìm tập hợp các cạnh của đồ thị đó sao cho:
- Tạo thành một cây bao gồm tất cả các đỉnh.
- Có tổng trọng số nhỏ nhất trong tất cả các cây có thể tạo ra từ đồ thị.
Lịch sử phát triển của thuật toán
Thuật toán Kruskal được giới thiệu lần đầu tiên vào năm 1956 bởi nhà toán học Joseph Kruskal. Thuật toán này dựa trên phương pháp tham lam (greedy algorithm), tối ưu hóa trọng số của cây khung bằng cách sắp xếp và chọn các cạnh có trọng số nhỏ nhất.
Sự khác biệt giữa Kruskal và Prim
Trong khi thuật toán Prim bắt đầu từ một đỉnh và mở rộng dần bằng cách thêm cạnh nhỏ nhất kết nối với cây hiện tại, thì thuật toán Kruskal không phụ thuộc vào điểm khởi đầu. Kruskal tập trung vào việc chọn các cạnh nhỏ nhất trên toàn bộ đồ thị.
II. Nguyên lý hoạt động của thuật toán Kruskal
Thuật toán này thuộc nhóm thuật toán tham lam (greedy algorithms). Chúng ta bắt đầu từ các cạnh có trọng số nhỏ nhất và tiếp tục thêm các cạnh cho đến khi đạt được mục tiêu.
Quy trình cơ bản của thuật toán Kruskal như sau:
- Sắp xếp tất cả các cạnh theo thứ tự tăng dần của trọng số.
- Chọn cạnh có trọng số nhỏ nhất và thêm vào cây khung. Nếu việc thêm cạnh tạo ra chu trình, hãy loại bỏ cạnh đó.
- Tiếp tục thêm các cạnh cho đến khi tất cả các đỉnh được bao gồm trong cây khung.
III. Giải thuật Kruskal
Các bước của thuật toán tìm cây phủ nhỏ nhất T của đồ thị liên thông có trọng số
như sau:
Bước 1: Đặt T = Ø (T rỗng không có cạnh)
Sắp xếp các cạnh của đồ thị theo thứ tự trọng số tăng dần vào tập Z
Bước 2: Trong khi (|T| < n-1) và Z≠Ø thức hiện:
- Tìm cạnh e có trọng số nhỏ nhất trong tập Z: Z= Z\{e}
- Nếu T ∪ {e} không tạo chu trình thì T = T ∪ {e}
IV. Độ phức tạp của thuật toán Kruskal
Độ phức tạp của thuật toán Kruskal là O(E*log V), trong đó E là số cạnh và V là số đỉnh trong đồ thị.
So với các thuật toán khác:
- Prim: Hiệu quả hơn với đồ thị dày.
- Dijkstra: Tập trung vào đường đi ngắn nhất thay vì cây khung nhỏ nhất.
V. Bài tập thuật toán Kruskal toán rời rạc
Bài 1: Áp dụng thuật toán Kruskal xác định cây khung nhỏ nhất của đồ thị với trọng số như hình vẽ:
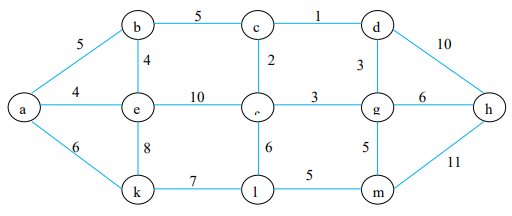
T = Ø, n=11
Lời giải

| Bước lặp | Cạnh được chọn và đưa vào T | Trọng số |
| 1 | C,D | 1 |
| 2 | C,F | 2 |
| 3 | D,G | 3 |
| 4 | Không chọn cạnh (F,G) vì tạo chu trình | |
| 5 | A,E | 4 |
| 6 | B,E | 4 |
| 7 | Không chọn cạnh (A,B) vì tạo chu trình | |
| 8 | B,C | 5 |
| 9 | G,M | 5 |
| 10 | L,M | 5 |
| 11 | A,K | 6 |
| 12 | Không chọn cạnh F,L vì tạo chu trình | |
| 13 | G,H | 6 |
| Tổng trọng số: | 41 |
Tập cạnh của cây khung nhỏ nhất cần tìm là T = {(C,D), (C,F), (D,G), (A,E),
(B,E), (B,C), (G,M), (L,M), (A,K), (G,H)}, có tổng trọng số là: 41. Cây khung này
như hình dưới :

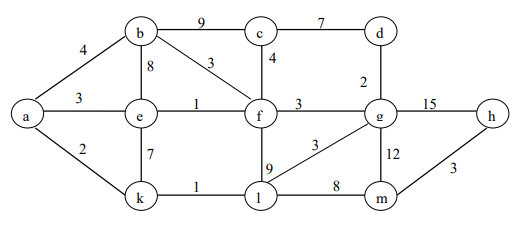
Bài 2: Hãy sử dụng thuật toán Kruskal tìm cây bao trùm nhỏ nhất của đồ thị G có chứa cạnh bc nhưng không chứa cạnh dh
Cây bao trùm nhỏ nhất không chứa cạnh dh của đồ thị G, ta loại cạnh dh ra
khỏi đồ thị, lúc này ta có đồ thị G’ với tập cạnh E’=E\{dh} như sau:

Khởi tạo T:= {(b,c)}.
Sắp xếp các cạnh của đồ thị theo thứ tự trọng số tăng dần trừ cạnh bc, ta có:
Z={(e,f), (k,l), (a,k), (d,g), (a,e), (b,f), (f,g), (h,m), (g,l), (a,b), (c,f), (c,d), (e,k),
(b,c), (l,m), (f,l), (g,m), (h,g) }.
| Bước lặp | Cạnh được chọn và đưa vào T | Trọng số |
| 1 | E,F | 1 |
| 2 | K,L | 1 |
| 3 | A,K | 2 |
| 4 | D,G | 2 |
| 5 | A,E | 3 |
| 6 | B,F | 3 |
| 7 | F,G | 3 |
| 8 | H,M | 3 |
| 9 | Không chọn cạnh G,L vì tạo chu trình | |
| 10 | Không chọn cạnh A,B vì tạo chu trình | |
| 11 | Không chọn cạnh C,F vì tạo chu trình | |
| 12 | Không chọn cạnh C,D vì tạo chu trình | |
| 13 | Không chọn cạnh E,K vì tạo chu trình | |
| 14 | Không chọn cạnh B,C vì tạo chu trình | |
| 15 | LM | 8 |
Tập cạnh của cây khung nhỏ nhất cần tìm là T={(B,C), (E,F), (K,L), (A,K), (D,G),
(A,E), (B,F), (F,G), (H,M), (L,M)}, trọng số nhỏ nhất bằng : 35. Cây khung được
vẽ như sau:
VI. Triển khai thuật toán Kruskal bằng C++
1. Phát biểu bài toán
Thuật toán sẽ xây dựng tập cạnh T của cây khung nhỏ nhất H=<V, T> theo từng bước như sau:
a. Sắp xếp các cạnh của đồ thị G theo thứ tự tăng dần của trọng số cạnh;
b. Xuất phát từ tập cạnh T=φ, ở mỗi bước, ta sẽ lần lượt duyệt trong danh sách các cạnh đã được sắp xếp, từ cạnh có trọng số nhỏ đến cạnh có trọng số lớn để tìm ra cạnh mà khi bổ sung nó vào T không tạo thành chu trình trong tập các cạnh đã được bổ sung vào T trước đó;
c. Thuật toán sẽ kết thúc khi ta thu được tập T gồm n-1 cạnh.
2. Mô tả thuật toán
void Kruskal() {
T = ∅; // Khởi tạo cây khung bé nhất T rỗng.
Trong khi (|T| < (n-1) và (E ≠ ∅)) {
Chọn cạnh e ∈ E có độ dài nhỏ nhất; // Chọn cạnh e từ E có độ dài nhỏ nhất.
E := E \ {e}; // Loại bỏ cạnh e khỏi tập cạnh còn lại.
Nếu (T ∪ {e} không tạo thành chu trình) // Nếu thêm cạnh e vào T không tạo thành chu trình.
T = T ∪ {e}; // Thêm cạnh e vào cây khung bé nhất T.
}
Nếu (|T| < n - 1)
Đồ thị không liên thông; // Đồ thị không liên thông.
}
3. Code thuật toán Kruskal c++
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <math.h>
#include <dos.h>
#define MAX 50
#define TRUE 1
#define FALSE 0
int n, m, minl, connect;
int dau[500],cuoi[500], w[500];
int daut[50], cuoit[50], father[50];
void Init(void){
int i; FILE *fp;
fp=fopen("baotrum1.in","r");
fscanf(fp, "%d%d", &n,&m);
printf("\n So dinh do thi:%d", n);
printf("\n So canh do thi:%d", m);
printf("\n Danh sach ke do thi:");
for(i=1; i<=m;i++){
fscanf(fp, "%d%d%d", &dau[i], &cuoi[i], &w[i]);
printf("\n Canh %d: %5d%5d%5d", i, dau[i], cuoi[i], w[i]);
}
fclose(fp);getch();
}
void Heap(int First, int Last){
int j, k, t1, t2, t3;
j=First;
while(j<=(Last/2)){
if( (2*j)<Last && w[2*j + 1]<w[2*j])
k = 2*j +1;
else
k=2*j;if(w[k]<w[j]){
t1=dau[j]; t2=cuoi[j]; t3=w[j];
dau[j]=dau[k]; cuoi[j]=cuoi[k]; w[j]=w[k];
dau[k]=t1; cuoi[k]=t2; w[k]=t3;
j=k;
}
else j=Last;
}
}
int Find(int i){
int tro=i;
while(father[tro]>0)
tro=father[tro];
return(tro);
}
void Union(int i, int j){
int x = father[i]+father[j];
if(father[i]>father[j]) {
father[i]=j;
father[j]=x;
}
else {
father[j]=i;
father[i]=x;
}
}
void Krusal(void){
int i, last, u, v, r1, r2, ncanh, ndinh;
for(i=1; i<=n; i++)
father[i]=-1;
for(i= m/2;i>0; i++)
Heap(i,m); last=m; ncanh=0; ndinh=0;minl=0;connect=TRUE;
while(ndinh<n-1 && ncanh<m){
ncanh=ncanh+1;
u=dau[1]; v=cuoi[1];
r1= Find(u); r2= Find(v);
if(r1!=r2) {
ndinh=ndinh+1; Union(r1,r2);
daut[ndinh]=u; cuoit[ndinh]=v;
minl=minl+w[1];
}
dau[1]=dau[last];
cuoi[1]=cuoi[last];
w[1]=w[last];
last=last-1;
Heap(1, last);
}
if(ndinh!=n-1) connect=FALSE;
}
void Result(void){
int i;
printf("\n Do dai cay khung nho nhat:%d", minl);
printf("\n Cac canh cua cay khung nho nhat:");
for(i=1; i<n; i++)
printf("\n %5d%5d",daut[i], cuoit[i]);
printf("\n");
}
void main(void){
clrscr(); Init();
Krusal();Result(); getch();
}
Tải full bài tập thực hành lập trình C/C++ có lời giải:
Lưu ý: Khum tải được tài liệu, liên hệ ngay fanpage để được hỗ trợ ạ!
Trên đây là bài tập và code thuật toán kruskal. Cảm ơn các bạn đã theo dõi toán rời rạc trên ttnguyen.net.
Bài viết liên quan:
Thuật toán cờ caro ma trận nxm c++