Thuật toán Dijkstra được sử dụng để giải quyết bài toán tìm đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại trên đồ thị có trọng số không âm. Sau đây hãy cùng TTnguyen tìm hiểu lý thuyết và một số bài tập thuật toán dijkstra có lời giải nhé.
Xem thêm:
bài tập toán rời rạc chương 1 có lời giải
I. Giới thiệu về thuật toán Dijkstra
Thuật toán Dijkstra (dijkstra algorithm) là một trong những thuật toán cơ bản và hiệu quả nhất để giải quyết bài toán tìm đường đi ngắn nhất trong một đồ thị. Thuật toán này giúp tìm đường đi ngắn nhất từ một đỉnh nguồn đến tất cả các đỉnh khác trong đồ thị có hướng hoặc vô hướng với trọng số không âm.
Ứng dụng thuật toán Dijkstra:
- Tìm đường đi ngắn nhất toán rời rạc trong các bài toán mạng máy tính.
- Giải quyết các bài toán thực tế như tìm lộ trình giao thông, định tuyến mạng.
- Là nền tảng cho nhiều thuật toán và bài toán phức tạp khác.
II. Nguyên lý hoạt động
Đầu vào: Đồ thị có hướng G=(V,E,W), đỉnh nguồn s.
Đầu ra: Khoảng cách ngắn nhất từ s đến các đỉnh khác, và đường đi tương ứng.
Thuật toán hoạt động dựa trên ý tưởng:
- Gán nhãn tạm thời cho tất cả các đỉnh trong đồ thị, trong đó nhãn của đỉnh nguồn bằng 0, và các đỉnh khác là vô hạn (∞)
- Chọn đỉnh có nhãn nhỏ nhất chưa được xử lý, cố định nhãn của đỉnh này.
- Cập nhật nhãn cho các đỉnh kề, nếu tìm được đường đi ngắn hơn qua đỉnh vừa cố định.
- Lặp lại bước 2 và 3 cho đến khi tất cả các đỉnh đã được cố định.
III. Bài tập thuật toán dijkstra có lời giải
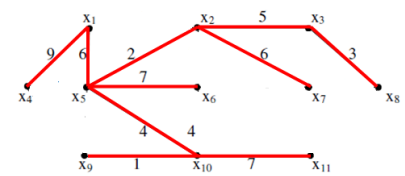
Tìm đường đi ngắn nhất từ đỉnh x1 đến các đỉnh còn lại của đồ thị vô hướng:

Lời giải

Từ bảng trên ta có đường đi ngắn nhất từ x1 đến các đỉnh là: X1X5X2 (độ dài 8); X1X4 (9); X1X5X2X3 (13); X1X5 (6); X1X5X6 (13); X1X5X2X7 (14); X1X5X2X3X8 (16); X1X5X10X9 (11); X1X5X10 (10); X1X5X10X11 (17)
Các đường đi được minh họa trên đồ thị sau:
Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại của đồ thị có hướng:
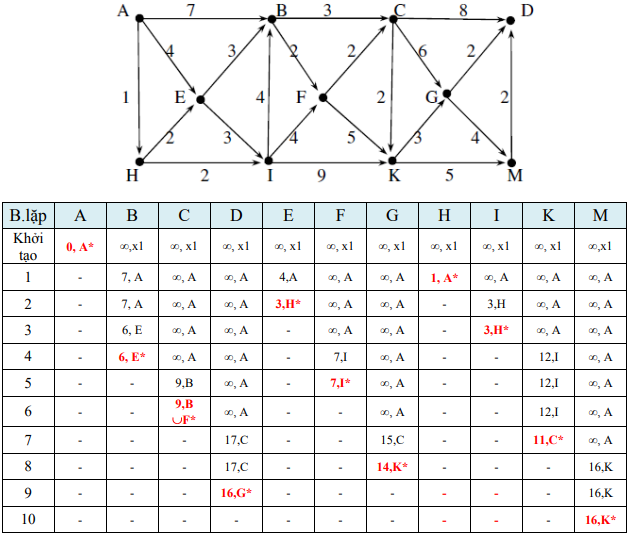
Từ bảng trên, ta có đường đi ngắn nhất từ A đến các đỉnh là: AHEB (6); AHIFC (9); AHIFKGD (16); AHE (3) AFHIF (7); AHIFCKG (14); AH (1); AHI (3); AHIFCK (11); AHIFCKM (16).

a. Tìm đường đi ngắn nhất từ x1 đến x14
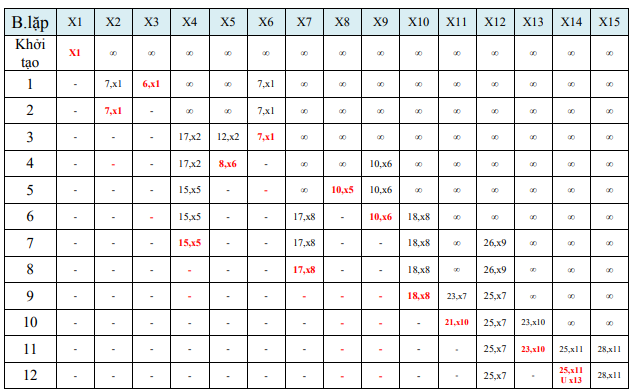
Từ bảng trên ta có đường đi ngắn nhất từ x1 đến x14 là: X1X6X5X8X10X13X14 hoặc X1X6X5X8X10X11X14 và độ dài là: 25.
b. Tìm đường đi ngắn nhất từ x1 đến x14 có chứa X8X9
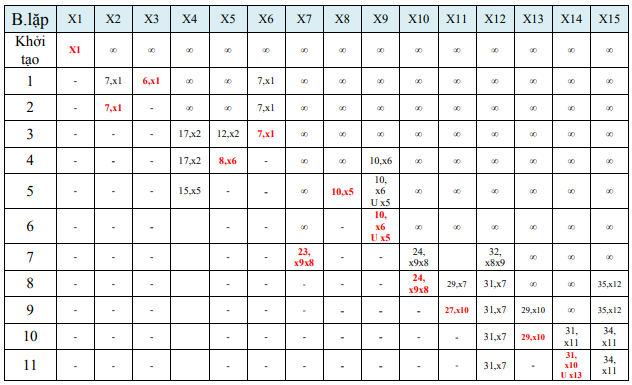
Từ bảng trên ta có đường đi ngắn nhất từ x1 đến x14 có chứa X8X9 là:x1x6x5x9x8x10x11x14 , hoặc x1x6x5x9x8x10x13x14 , hoặc x1x6x9x8x10x11x14 , hoặc x1x6x9x8x10x13x14 với chiều dài là: 31
c. Tìm đường đi ngắn nhất từ x1 đến x14 có chứa đỉnh X7
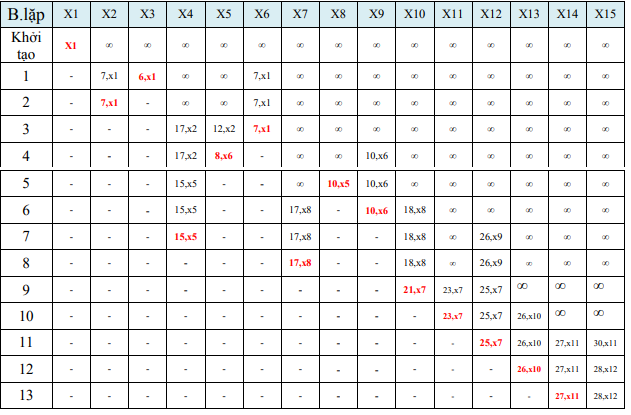
Vậy đường đi ngắn nhất từ x1 đến x14 có chứa đỉnh X7 là: X1 X6 X5 X8 X7 X11 X14, và độ dài đường đi bằng: 27
IV. Cài đặt thuật toán Dijkstra trong C++
1. Mô tả thuật toán
Các bước chính của thuật toán Dijkstra để tìm đường đi ngắn nhất từ đỉnh a đến đỉnh z trên đồ thị G=(V,E,W) được mô tả như sau:
Bước 1 : T=V; Da = 0; Di = ∞, Vi ≠ a.
Bước 2 : Lặp cho đến khi z ∉T:
– Lấy ra khỏi T đỉnh Vi có Di nhỏ nhất
– Đánh nhãn lại cho mọi Vj kề Vi và Vj T ∈ theo công thức: Dj = min{Dj, Di+Wij}
Thuật toán có thể được mô tả bằng thủ tục Dijkstra như sau:
void Dijkstra(void)
/*Đầu vào G=(V, E) với n đỉnh có ma trận trọng số A[u,v]≥ 0; s∈V */
/*Đầu ra là khoảng cách nhỏ nhất từ s đến các đỉnh còn lại d[v]: v∈V*/
/*Truoc[v] ghi lại đỉnh trước v trong đường đi ngắn nhất từ s đến v*/
{
/* Bước 1: Khởi tạo nhãn tạm thời cho các đỉnh*/
for (v∈ V) {
d[v] = A[s, v];
truoc[v] = s;
}
d[s] = 0;
T = V\ {
s
}; /*T là tập đỉnh có nhãn tạm thời*/
/* Bước lặp */
while (T != φ) {
Tìm đỉnh u∈ T sao cho d[u] = min {
d[z] | z∈ T
};
T = T\ {
u
}; /*cố định nhãn đỉnh u*/ ;
For(v∈ T) {
/* Gán lại nhãn cho các đỉnh trong T*/
If(d[v] > d[u] + A[u, v]) {
d[v] = d[u] + A[u, v];
truoc[v] = u;
}
}
}
}
2. Code thuật toán dijkstra
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <math.h>
#include <dos.h>
#define MAX 50
#define TRUE 1
#define FALSE 0
int n, s, t;
char chon;
int truoc[MAX], d[MAX], CP[MAX][MAX];
int final[MAX];
void Init(void) {
FILE * fp;
int i, j;
fp = fopen(“ijk1.in”, ”r”);
fscanf(fp, ” % d”, & n);
printf(“\n So dinh: % d”, n);
printf(“\n Ma tran khoang cach: ”);
for (i = 1; i <= n; i++) {
printf(“\n”);
for (j = 1; j <= n; j++) {
fscanf(fp, “ % d”, & CP[i][j]);
printf(“ % 3 d”, CP[i][j]);
if (CP[i][j] == 0) CP[i][j] = 32000;
}
}
fclose(fp);
}
void Result(void) {
int i, j;
printf(“\n Duong di ngan nhat tu % d den % d la\ n”, s, t);
printf(“ % d <= ”, t);
i = truoc[t];
while (i != s) {
printf(“ % d <= ”, i);
i = truoc[i];
}
printf(“ % d”, s);
printf(“\n Do dai duong di la: % d”, d[t]);
getch();
}
void Dijkstra(void) {
int v, u, minp;
printf(“\n Tim duong di tu s = ”);
scanf(“ % d”, & s);
printf(“den“);
scanf(“ % d”, & t);
for (v = 1; v <= n; v++) {
d[v] = CP[s][v];
truoc[v] = s;
final[v] = FALSE;
}
truoc[s] = 0;
d[s] = 0;
final[s] = TRUE;
while (!final[t]) {
minp = 2000;
for (v = 1; v <= n; v++) {
if ((!final[v]) && (minp > d[v])) {
u = v;
minp = d[v];
}
}
final[u] = TRUE; // u- la dinh co nhan tam thoi nho nhat
if (!final[t]) {
for (v = 1; v <= n; v++) {
if ((!final[v]) && (d[u] + CP[u][v] < d[v])) {
d[v] = d[u] + CP[u][v];
truoc[v] = u;
}
}
}
}
}
void main(void) {
clrscr();
Init();
Dijkstra();
Result();
getch();
}
Trên đây là bài tập thuật toán dijkstra toán rời rạc và cách cách đặt thuật toán trên ngôn ngữ lập trình C++. Cảm ơn các bạn đã theo dõi trên ttnguyen.net.
Bài viết cùng chủ đề: